Hoe Bereken Je Kubieke Meters

Het berekenen van kubieke meters, oftewel m³, is een fundamentele vaardigheid in diverse disciplines, van bouwkunde en logistiek tot tuinieren en zelfs koken. Of je nu de hoeveelheid beton voor een fundering wilt schatten, de capaciteit van een container berekent, of simpelweg wilt weten hoeveel aarde je nodig hebt voor een bloembak, een goede beheersing van deze berekening is essentieel. Deze gids biedt een gedetailleerde uitleg van hoe je kubieke meters berekent, inclusief praktische voorbeelden en relevante context.

Wat Zijn Kubieke Meters?

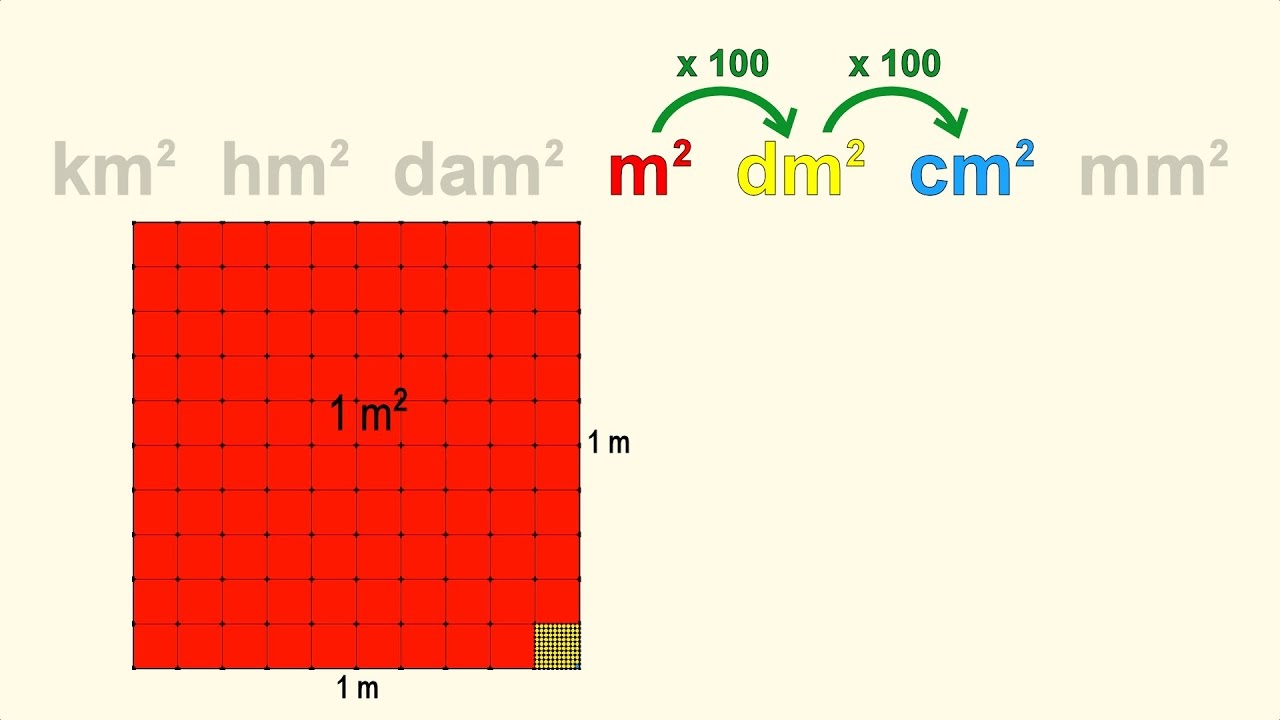
Een kubieke meter (m³) is de standaardeenheid voor volume in het Internationale Stelsel van Eenheden (SI). Stel je een perfecte kubus voor met zijden van precies één meter. De ruimte binnen die kubus is één kubieke meter. Het is dus een maat voor hoeveel ruimte iets inneemt in drie dimensies: lengte, breedte en hoogte.

De Basisformule voor het Berekenen van Kubieke Meters

De meest eenvoudige manier om kubieke meters te berekenen is met de volgende formule:

Volume (m³) = Lengte (m) x Breedte (m) x Hoogte (m)

Deze formule geldt voor regelmatige, rechthoekige vormen zoals dozen, containers, en kamers. Het is cruciaal dat alle metingen in dezelfde eenheid zijn, namelijk meters. Als je bijvoorbeeld maten in centimeters of millimeters hebt, moet je deze eerst omzetten naar meters voordat je de berekening uitvoert.

Voorbeeld 1: Een rechthoekige kamer

Stel je voor dat je de inhoud van een kamer wilt berekenen. De kamer is 4 meter lang, 3 meter breed en 2.5 meter hoog. De berekening is als volgt:

Volume = 4 m x 3 m x 2.5 m = 30 m³

De kamer heeft dus een volume van 30 kubieke meter.

Omrekenen naar Meters

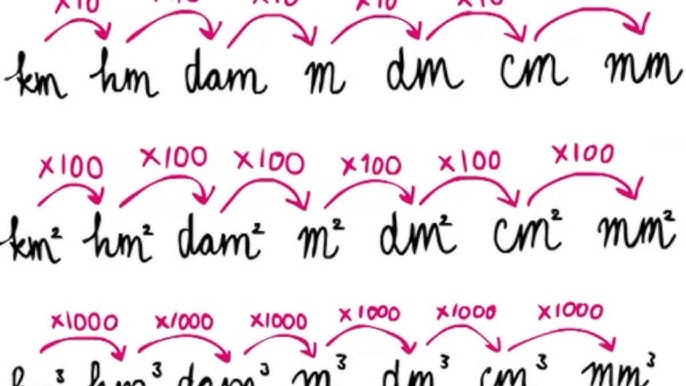
Zoals eerder genoemd, is het essentieel dat alle metingen in meters zijn voordat je de formule toepast. Hier zijn enkele veelvoorkomende omrekeningen:

1 meter (m) = 100 centimeter (cm)
1 meter (m) = 1000 millimeter (mm)
1 centimeter (cm) = 0.01 meter (m)
1 millimeter (mm) = 0.001 meter (m)

Voorbeeld 2: Omrekenen en Berekenen

Je hebt een doos die 150 cm lang, 80 cm breed en 60 cm hoog is. Om de inhoud in kubieke meters te berekenen, moet je eerst de afmetingen omzetten naar meters:

Lengte: 150 cm = 1.5 m
Breedte: 80 cm = 0.8 m
Hoogte: 60 cm = 0.6 m

Vervolgens pas je de formule toe:

Volume = 1.5 m x 0.8 m x 0.6 m = 0.72 m³

De doos heeft dus een inhoud van 0.72 kubieke meter.

Berekenen van Kubieke Meters voor Onregelmatige Vormen

Niet alles is een perfecte rechthoek. Voor onregelmatige vormen is de berekening complexer en vereist vaak benaderingen of specifieke formules afhankelijk van de vorm.

Cilinders

Voor een cilinder is de formule:

Volume = πr²h

Waar:

π (pi) ≈ 3.14159
r = straal van de basis (de helft van de diameter)
h = hoogte van de cilinder

Voorbeeld 3: Een cilindervormige tank

Een waterreservoir heeft een diameter van 2 meter en een hoogte van 3 meter. Om de inhoud te berekenen:

Straal (r) = 2 m / 2 = 1 m

Volume = 3.14159 x (1 m)² x 3 m = 9.42477 m³

De tank kan ongeveer 9.42 kubieke meter water bevatten.

Kegels

Voor een kegel is de formule:

Volume = (1/3)πr²h

Waar:

π (pi) ≈ 3.14159
r = straal van de basis
h = hoogte van de kegel

Voorbeeld 4: Een kegelvormige zandhoop

Een zandhoop heeft een diameter van 4 meter en een hoogte van 1.5 meter. Om de inhoud te berekenen:

Straal (r) = 4 m / 2 = 2 m

Volume = (1/3) x 3.14159 x (2 m)² x 1.5 m = 6.28318 m³

De zandhoop heeft ongeveer een volume van 6.28 kubieke meter.

Complexe Vormen: Benadering en Integratie

Voor objecten met nog complexere, onregelmatige vormen, is het vaak onmogelijk om een precieze berekening te maken met eenvoudige formules. In deze gevallen zijn er verschillende methoden om een benadering te krijgen:

Verdelen in Simpelere Vormen: Probeer het object op te delen in meerdere, eenvoudigere vormen (zoals rechthoeken, cilinders, etc.) waarvan je het volume wel kunt berekenen. Tel vervolgens de volumes van deze afzonderlijke vormen bij elkaar op. Dit is een benadering, maar kan in veel gevallen voldoende nauwkeurig zijn.
Waterverplaatsing (Archimedes' Principe): Als het mogelijk is, kun je het object in een bak met water onderdompelen en meten hoeveel water het object verplaatst. De hoeveelheid verplaatst water is gelijk aan het volume van het object. Dit werkt alleen voor massieve objecten die niet oplossen in water.
3D-Scanning en Software: Voor zeer complexe vormen kan 3D-scanning worden gebruikt om een digitaal model van het object te maken. Speciale software kan vervolgens het volume van het model berekenen. Dit is een nauwkeurige, maar duurdere methode.

Praktische Toepassingen

Het berekenen van kubieke meters is van cruciaal belang in veel verschillende situaties:

Bouw en Constructie: Voor het schatten van de hoeveelheid beton, zand, grind of andere materialen die nodig zijn voor een project. Een verkeerde schatting kan leiden tot aanzienlijke verspilling of vertraging.
Logistiek en Transport: Voor het bepalen van de capaciteit van vrachtwagens, containers en magazijnen. Dit is belangrijk voor het optimaliseren van transport en opslagkosten.
Tuinieren en Landschapsarchitectuur: Voor het berekenen van de hoeveelheid aarde, mulch of compost die nodig is voor een tuinbed of een landschapsproject.
Verwarming en Ventilatie: Voor het dimensioneren van verwarmings- en ventilatiesystemen. De grootte van de ruimte (in kubieke meters) bepaalt de benodigde capaciteit van het systeem.
Aquaria en Vijvers: Voor het berekenen van de hoeveelheid water die een aquarium of vijver kan bevatten. Dit is belangrijk voor het kiezen van de juiste filter en andere apparatuur.

Voorbeeld uit de praktijk: Beton storten

Stel, je wilt een betonnen fundering storten voor een tuinhuis. De fundering moet 5 meter lang, 3 meter breed en 0.15 meter dik zijn. Hoeveel beton heb je nodig?

Volume = 5 m x 3 m x 0.15 m = 2.25 m³

Je hebt dus 2.25 kubieke meter beton nodig. Houd er rekening mee dat je waarschijnlijk iets meer moet bestellen om rekening te houden met verspilling en onregelmatigheden.

Conclusie en Aanbevelingen

Het berekenen van kubieke meters is een essentiële vaardigheid met toepassingen in talloze vakgebieden. Door de basisformule en de nodige omrekeningen te beheersen, kun je nauwkeurige schattingen maken en onnodige kosten en vertragingen voorkomen.

Oefen regelmatig met verschillende voorbeelden om je vaardigheden te verbeteren. Gebruik online rekenmachines of spreadsheets om complexere berekeningen te vereenvoudigen. En bovenal, controleer altijd je metingen om fouten te minimaliseren. Door deze stappen te volgen, kun je met vertrouwen kubieke meters berekenen voor al je projecten.