Hoe Bereken Je Q1 En Q3

Laten we eerlijk zijn, statistiek kan soms voelen alsof je een doolhof in loopt zonder plattegrond. Je bent niet de enige die worstelt met concepten als Q1 en Q3. Misschien zit je vast aan een schoolopdracht, of probeer je de verkoopcijfers van je bedrijf te analyseren. Hoe dan ook, die kwartielen kunnen je flink hoofdbrekens bezorgen. Ik snap het helemaal!

Maar geloof me, het is niet zo ingewikkeld als het lijkt. Zodra je de basisprincipes begrijpt, zul je merken dat het berekenen van Q1 en Q3 je een krachtig inzicht geeft in de verdeling van data. Dit is niet alleen relevant voor statistici; denk aan marketingteams die hun doelgroep beter willen begrijpen, HR-afdelingen die salarisverdelingen analyseren, of zelfs de gemiddelde persoon die zijn persoonlijke financiën in kaart wil brengen.

Deze uitleg gaat je helpen. We gaan dieper in op de materie, zodat je straks met vertrouwen Q1 en Q3 kunt berekenen. Geen vage formules, maar een heldere uitleg met praktische voorbeelden. Dus laten we beginnen!

Wat zijn Q1 en Q3 eigenlijk?

Voordat we beginnen met rekenen, is het cruciaal om te begrijpen wat Q1 en Q3 *precies* zijn. Zie het als het opdelen van een taart.

Q1 (Eerste Kwartiel): Dit is het punt waar 25% van je data onder ligt. Met andere woorden, het scheidt de laagste 25% van de data van de rest. Stel je voor: je hebt een lijst met de leeftijden van alle deelnemers aan een workshop. Q1 is de leeftijd waaronder 25% van de deelnemers valt.
Q3 (Derde Kwartiel): Dit is het punt waar 75% van je data onder ligt. Het scheidt dus de hoogste 25% van de data van de lagere 75%. In ons voorbeeld met de workshop, zou Q3 de leeftijd zijn waaronder 75% van de deelnemers valt.

Het kwartiel waar mensen vaak van op de hoogte zijn, maar zelden benoemen is Q2. Q2 (Tweede Kwartiel): Dit is hetzelfde als de mediaan, en verdeelt de data precies in twee helften. 50% van de data ligt er onder, 50% er boven.

Het gebied tussen Q1 en Q3 wordt de interkwartielafstand (IQR) genoemd. De IQR geeft inzicht in de spreiding van de middelste 50% van de data. Een grote IQR betekent dat de data in het midden meer verspreid is, terwijl een kleine IQR betekent dat de data in het midden dichter bij elkaar ligt.

Waarom is dit belangrijk?

Q1 en Q3 geven je een veel beter beeld van de data dan alleen het gemiddelde. Het gemiddelde kan namelijk misleidend zijn als er extreme waarden (outliers) in de dataset zitten. Denk bijvoorbeeld aan het gemiddelde inkomen in een land. Een paar extreem hoge inkomens kunnen het gemiddelde flink omhoog trekken, waardoor het niet meer representatief is voor de meeste mensen. Q1 en Q3 zijn minder gevoelig voor outliers en geven daarom een realistischer beeld van de verdeling.

Stel je voor dat je een webshop hebt. Door Q1 en Q3 van de bestelwaarden te berekenen, kun je beter begrijpen wat de typische bestelwaarde is en welke bestellingen extreem hoog of laag zijn. Dit kan je helpen om gerichte marketingcampagnes op te zetten of om frauduleuze bestellingen te detecteren.

Hoe bereken je Q1 en Q3? Stap voor stap.

Oké, genoeg theorie. Nu gaan we aan de slag met de berekening. Het is belangrijk om de stappen zorgvuldig te volgen.

Sorteer je data: De eerste stap is om je data van klein naar groot te sorteren. Dit is essentieel, anders kloppen je kwartielen niet. Stel, je hebt de volgende dataset: 12, 5, 8, 21, 15. Na het sorteren krijg je: 5, 8, 12, 15, 21.
Bepaal de mediaan (Q2): De mediaan is de middelste waarde in de dataset. Als je een oneven aantal waarden hebt, is de mediaan de middelste waarde. In ons voorbeeld is dat 12. Als je een even aantal waarden hebt, is de mediaan het gemiddelde van de twee middelste waarden. Stel, je hebt de volgende dataset: 5, 8, 12, 15. De mediaan is dan (8+12)/2 = 10.
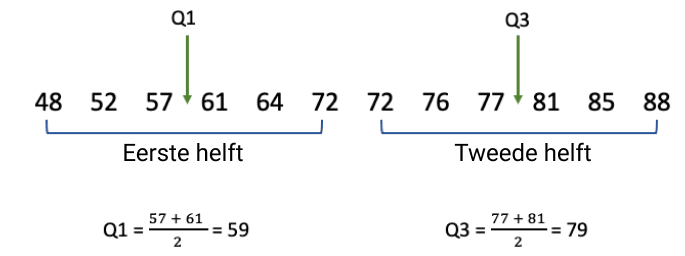
Bereken Q1: Q1 is de mediaan van de *onderste* helft van de data. Let op: als je mediaan een waarde uit je dataset was, dan neem je deze *niet* mee in de onderste helft. In ons eerste voorbeeld (5, 8, 12, 15, 21) is de mediaan 12. De onderste helft is dus 5, 8. De mediaan hiervan (Q1) is (5+8)/2 = 6.5.
Bereken Q3: Q3 is de mediaan van de *bovenste* helft van de data. Ook hier geldt: als je mediaan een waarde uit je dataset was, dan neem je deze *niet* mee in de bovenste helft. In ons eerste voorbeeld (5, 8, 12, 15, 21) is de mediaan 12. De bovenste helft is dus 15, 21. De mediaan hiervan (Q3) is (15+21)/2 = 18.

Een extra voorbeeld

Laten we nog een voorbeeld bekijken om het helemaal duidelijk te maken.

Dataset: 2, 4, 7, 1, 9, 5, 3, 8, 6

Sorteer: 1, 2, 3, 4, 5, 6, 7, 8, 9
Mediaan (Q2): De mediaan is 5.
Q1: De onderste helft (zonder de mediaan) is 1, 2, 3, 4. De mediaan hiervan (Q1) is (2+3)/2 = 2.5.
Q3: De bovenste helft (zonder de mediaan) is 6, 7, 8, 9. De mediaan hiervan (Q3) is (7+8)/2 = 7.5.

Alternatieve methoden en software

Hoewel de bovenstaande methode het meest intuïtief is, zijn er andere methoden om Q1 en Q3 te berekenen. Sommige statistische softwarepakketten gebruiken net iets andere formules. Het is belangrijk om te weten dat deze verschillende methoden kleine verschillen in de uitkomst kunnen geven, vooral bij kleine datasets. De basis blijft echter hetzelfde: het opdelen van de data in kwartielen.

Software

Gelukkig hoef je niet altijd alles met de hand te berekenen. Er zijn tal van softwarepakketten die je kunnen helpen. Denk aan:

Excel: Excel heeft een ingebouwde functie genaamd "KWARTIEL" (of "QUARTILE" in de Engelse versie). Je kunt eenvoudig de data selecteren en aangeven welk kwartiel je wilt berekenen (1 voor Q1, 3 voor Q3).
SPSS: SPSS is een krachtig statistisch softwarepakket dat veel gebruikt wordt in de wetenschap. Het biedt uitgebreide mogelijkheden voor het analyseren van data, waaronder het berekenen van kwartielen.
R: R is een programmeertaal die veel gebruikt wordt voor statistische analyse. Het biedt een breed scala aan functies en pakketten voor het berekenen van kwartielen en andere statistische maatstaven.
Python (met bibliotheken zoals NumPy en Pandas): Python is een veelzijdige programmeertaal die ook geschikt is voor statistische analyse. Met behulp van bibliotheken zoals NumPy en Pandas kun je eenvoudig kwartielen berekenen.

Het voordeel van het gebruik van software is dat je snel grote hoeveelheden data kunt analyseren. Het is echter wel belangrijk om te begrijpen *hoe* de software de kwartielen berekent, zodat je de resultaten correct kunt interpreteren.

Misvattingen en counterpoints

Een veelvoorkomende misvatting is dat Q1 en Q3 altijd *waarden* in de dataset moeten zijn. Dat is niet het geval! Zoals je in de voorbeelden hebt gezien, kan Q1 of Q3 een waarde zijn die *tussen* twee waarden in de dataset ligt. Dit is volkomen normaal en correct.

Een ander punt dat vaak ter sprake komt, is de "juiste" manier om Q1 en Q3 te berekenen. Zoals eerder genoemd, zijn er verschillende methoden. Sommige mensen beweren dat de ene methode "beter" is dan de andere. In werkelijkheid is er geen eenduidig "juist" antwoord. De beste methode hangt af van de specifieke context en de grootte van de dataset. Zolang je consistent bent in je aanpak en de methode duidelijk documenteert, is er geen probleem.

Sommige mensen beargumenteren ook dat kwartielen overbodig zijn, omdat er andere statistische maatstaven zijn, zoals standaarddeviatie. Hoewel standaarddeviatie zeker nuttig is, geeft het een ander soort informatie dan kwartielen. Kwartielen zijn vooral handig voor het identificeren van outliers en het visualiseren van de verdeling van de data, terwijl standaarddeviatie meer gericht is op de spreiding rondom het gemiddelde.

De impact in de echte wereld

Het berekenen van Q1 en Q3 is niet alleen een theoretische oefening. Het heeft een enorme impact in de echte wereld, in verschillende sectoren.

Financiën: Beleggers gebruiken kwartielen om het risico van beleggingen te beoordelen. Door de spreiding van de rendementen te analyseren, kunnen ze bepalen hoe volatiel een bepaalde belegging is.
Gezondheidszorg: Artsen en onderzoekers gebruiken kwartielen om de effectiviteit van behandelingen te evalueren. Door de verdeling van de resultaten te bekijken, kunnen ze bepalen of een behandeling significant beter is dan een andere.
Onderwijs: Docenten gebruiken kwartielen om de prestaties van studenten te beoordelen. Door de verdeling van de scores te bekijken, kunnen ze bepalen welke studenten extra ondersteuning nodig hebben.
Marketing: Marketeers gebruiken kwartielen om hun doelgroep beter te begrijpen. Door de verdeling van demografische gegevens, aankoopgedrag en andere factoren te analyseren, kunnen ze gerichte marketingcampagnes opzetten.
Human Resources: HR-professionals gebruiken kwartielen om salarisverdelingen te analyseren. Dit helpt om ervoor te zorgen dat salarissen eerlijk en competitief zijn.

De mogelijkheden zijn eindeloos. Door de data te analyseren met behulp van kwartielen, kun je patronen en trends ontdekken die anders verborgen zouden blijven.

Blijf Oefenen

De beste manier om Q1 en Q3 echt onder de knie te krijgen, is door te oefenen. Zoek datasets online (bijvoorbeeld op Kaggle of data.overheid.nl) en probeer de kwartielen te berekenen. Gebruik zowel de handmatige methode als software om de resultaten te vergelijken. Hoe meer je oefent, hoe zelfverzekerder je zult worden.

Hopelijk heb je nu een helder beeld van hoe je Q1 en Q3 kunt berekenen en waarom dit belangrijk is. Het is een waardevolle skill die je kunt toepassen in verschillende situaties. Vergeet niet: oefening baart kunst!

Nu je dit gelezen hebt, welke dataset ga jij als eerste analyseren en welke inzichten hoop je te ontdekken?