Hoe Doe Je Breuken Plus Elkaar

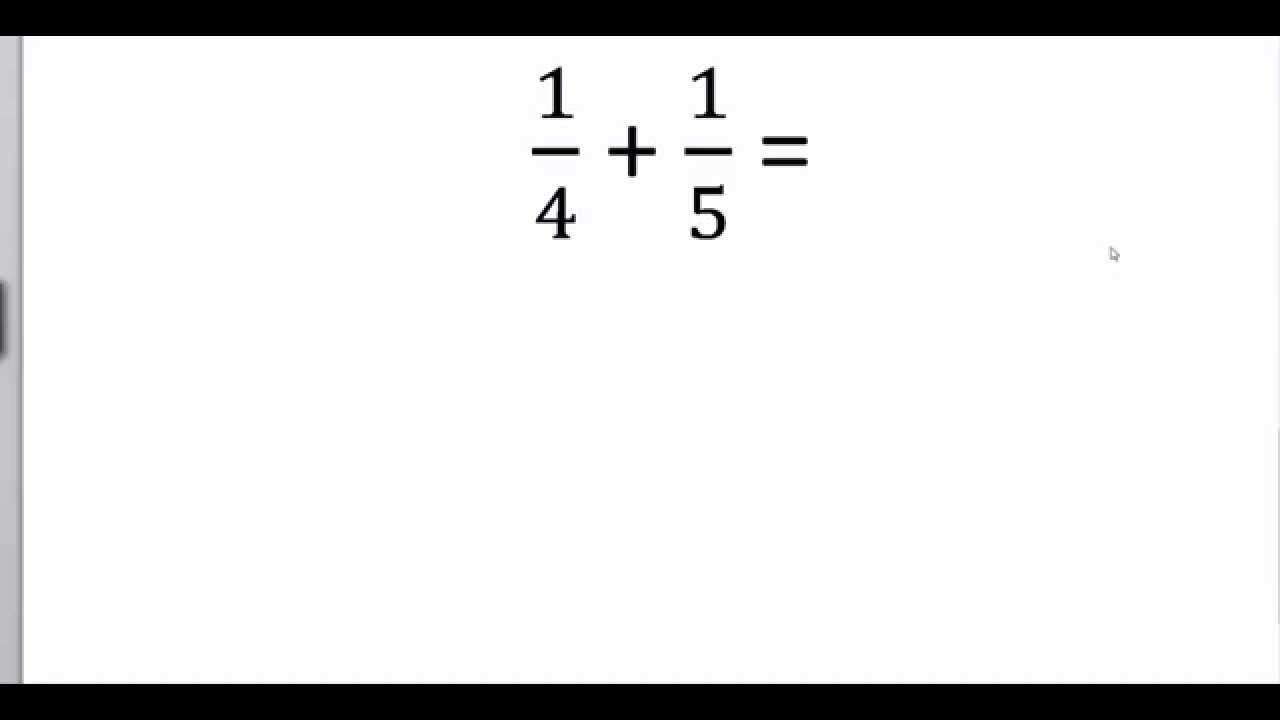
Herken je dat? Je zit te worstelen met een wiskundesom, zweetdruppels op je voorhoofd, en het enige dat je voor elkaar krijgt is meer verwarring. Breuken optellen, het lijkt soms wel een onmogelijke opgave. Maar geloof me, je bent niet alleen. Veel mensen vinden het lastig, en dat is helemaal oké! Deze gids is er om je te helpen die drempel te overwinnen en breuken optellen eindelijk onder de knie te krijgen. We gaan het stap voor stap doen, met duidelijke uitleg en praktische voorbeelden.

Waarom zijn breuken zo belangrijk?

Je denkt misschien: "Wanneer ga ik dit ooit in het echte leven gebruiken?" Nou, vaker dan je denkt! Breuken kom je overal tegen:

Koken en bakken: Recepten vragen vaak om 1/2 kopje bloem of 1/4 theelepel zout.
Tijd: Een kwartier is 1/4 van een uur.
Geld: De helft van een euro is 50 cent.
Metingen: Een halve meter stof of 3/4 liter melk.

Zonder breuken zouden veel alledaagse dingen veel lastiger worden! Begrijpen hoe ze werken, en hoe je ze kan optellen, is dus een waardevolle vaardigheid.

De basis: Wat is een breuk?

Laten we even terug naar de basis. Een breuk bestaat uit twee delen:

De teller: Het getal boven de streep (bijvoorbeeld 1 in 1/2). Het geeft aan hoeveel delen je hebt.
De noemer: Het getal onder de streep (bijvoorbeeld 2 in 1/2). Het geeft aan in hoeveel gelijke delen het geheel is verdeeld.

Een breuk representeert dus een deel van een geheel. In het voorbeeld van 1/2, heb je één deel van een geheel dat in twee gelijke delen is verdeeld. Je hebt dus de helft.

De uitdaging: Ongelijksoortige noemers

Het optellen van breuken is relatief eenvoudig als de noemers gelijk zijn. Bijvoorbeeld: 1/4 + 2/4 = 3/4. Je telt simpelweg de tellers bij elkaar op, en de noemer blijft hetzelfde.

Maar wat als de noemers verschillend zijn? Bijvoorbeeld: 1/2 + 1/3. Hier wordt het ingewikkelder. Je kan ze niet zomaar optellen!

Waarom kunnen we ze niet zomaar optellen?

Stel je voor: je hebt een pizza. Je snijdt de ene pizza in tweeën (1/2) en de andere in drieën (1/3). Het zijn verschillende stukken! Je kan ze niet zomaar bij elkaar gooien en zeggen dat je "twee stukken" hebt. Je moet ze eerst gelijk maken.

De oplossing: Gelijksoortig maken!

De sleutel tot het optellen van breuken met verschillende noemers is het gelijksoortig maken van de breuken. Dit betekent dat je de breuken moet omzetten naar equivalente breuken met dezelfde noemer. Dit doen we door de kleinste gemeenschappelijke veelvoud (KGV) van de noemers te vinden.

Hoe vind je de KGV?

De KGV is het kleinste getal dat een veelvoud is van beide noemers. Er zijn verschillende manieren om de KGV te vinden:

Uitschrijven van de veelvouden: Schrijf de veelvouden van beide noemers op, totdat je een getal vindt dat in beide rijen voorkomt.
Priemfactorisatie: Ontbind beide noemers in priemfactoren. De KGV is het product van alle priemfactoren, waarbij je de hoogste macht van elke factor neemt.

Laten we teruggaan naar ons voorbeeld: 1/2 + 1/3

De noemers zijn 2 en 3.
De veelvouden van 2 zijn: 2, 4, 6, 8, 10...
De veelvouden van 3 zijn: 3, 6, 9, 12, 15...
De KGV van 2 en 3 is dus 6.

Breuken omzetten naar een gemeenschappelijke noemer

Nu we de KGV hebben gevonden (6), moeten we de breuken omzetten naar breuken met noemer 6.

1/2: Om van noemer 2 naar noemer 6 te gaan, moeten we vermenigvuldigen met 3 (2 x 3 = 6). We moeten dan ook de teller vermenigvuldigen met 3 (1 x 3 = 3). Dus 1/2 wordt 3/6.
1/3: Om van noemer 3 naar noemer 6 te gaan, moeten we vermenigvuldigen met 2 (3 x 2 = 6). We moeten dan ook de teller vermenigvuldigen met 2 (1 x 2 = 2). Dus 1/3 wordt 2/6.

Nu hebben we de som: 3/6 + 2/6

Eindelijk optellen!

Nu de noemers gelijk zijn, kunnen we de tellers optellen: 3 + 2 = 5

De uitkomst is dus 5/6.

Voorbeelden en oefeningen

Laten we nog een paar voorbeelden bekijken:

1/4 + 1/8: De KGV van 4 en 8 is 8. Dus 1/4 wordt 2/8. De som wordt 2/8 + 1/8 = 3/8.
2/5 + 1/10: De KGV van 5 en 10 is 10. Dus 2/5 wordt 4/10. De som wordt 4/10 + 1/10 = 5/10. Dit kan je vereenvoudigen tot 1/2.
1/3 + 1/4: De KGV van 3 en 4 is 12. Dus 1/3 wordt 4/12 en 1/4 wordt 3/12. De som wordt 4/12 + 3/12 = 7/12.

Oefening baart kunst! Probeer de volgende sommen zelf op te lossen:

1/2 + 1/4
2/3 + 1/6
1/5 + 2/15

Counterargumenten: "Is er geen makkelijkere manier?"

Er zijn zeker trucs en shortcuts die je kan gebruiken, zoals het gebruik van een rekenmachine. Maar het is essentieel om het concept te begrijpen. Zonder begrip ben je afhankelijk van de rekenmachine en kan je geen problemen oplossen als je er geen tot je beschikking hebt. Bovendien helpt het begrip van breuken je bij het ontwikkelen van je wiskundig inzicht, wat nuttig is voor andere wiskundige concepten.

Een andere veelgehoorde opmerking is dat breuken "ouderwets" zijn en dat decimale getallen handiger zijn. Hoewel decimale getallen inderdaad vaak gebruikt worden, zijn breuken soms preciezer en bieden ze een duidelijker beeld van de verhouding. Denk bijvoorbeeld aan het delen van een pizza: 1/3 is veel duidelijker dan 0.3333...

Tips en trucs

Vereenvoudig breuken: Voordat je breuken optelt, is het handig om ze te vereenvoudigen. Dit maakt de getallen kleiner en makkelijker om mee te werken.
Gebruik visualisaties: Teken cirkels of rechthoeken en verdeel ze in stukken om de breuken visueel voor te stellen.
Oefen regelmatig: Wiskunde is een vaardigheid die je moet onderhouden. Doe regelmatig oefeningen om je kennis op peil te houden.

De volgende stap

Hopelijk heb je nu een beter begrip van hoe je breuken moet optellen. Het is belangrijk om te onthouden dat oefening essentieel is. Blijf oefenen en experimenteren met verschillende breuken. Probeer het bijvoorbeeld eens toe te passen in de keuken tijdens het koken! Misschien vind je het wel leuk.

Denk er eens over na: waar ben je breuken tegengekomen in je eigen leven, buiten school? Hoe zou je ze nu anders benaderen met de kennis die je nu hebt?

Heb je nog vragen? Laat ze achter in de comments!