Hoe Maak Je Breuken Gelijknamig

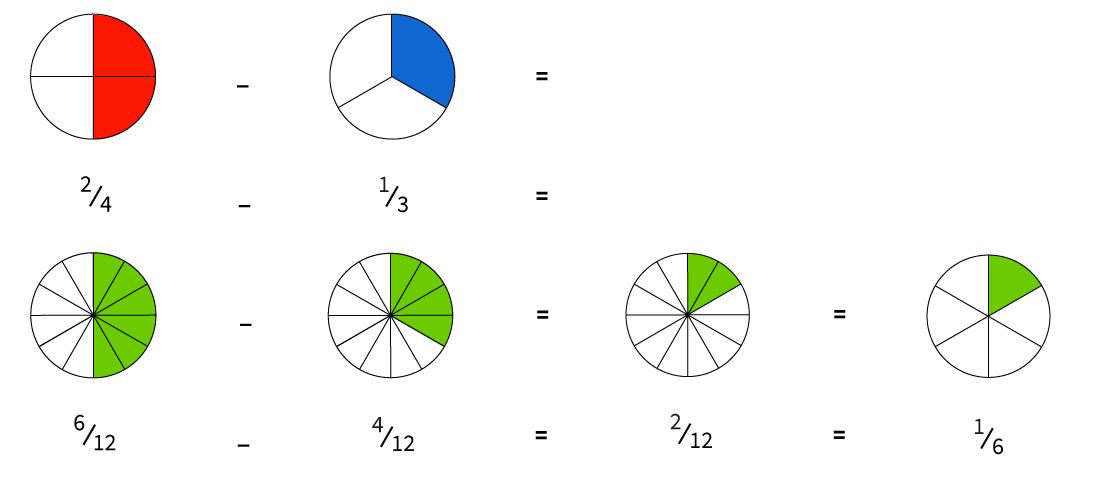
Heb je ooit geprobeerd om een recept te verdubbelen en werd je gek van alle breuken? Of misschien worstel je al jaren met die simpele rekensom op de spaarbankrekening? Weet je, je bent niet alleen. Veel mensen vinden breuken lastig, en het gelijknamig maken ervan kan als een extra hindernis voelen. Maar geen zorgen, na het lezen van dit artikel, zul je merken dat het eigenlijk best wel te doen is!

Waarom is het Gelijknamig Maken van Breuken Belangrijk?

Breuken gelijknamig maken betekent simpelweg dat je breuken met verschillende noemers (het getal onder de streep) omzet naar breuken met dezelfde noemer. Waarom zou je dat willen? Nou, denk er eens over na: het is veel gemakkelijker om appels met appels te vergelijken dan appels met peren, toch? Hetzelfde geldt voor breuken!

Door breuken gelijknamig te maken, kun je:

• Ze gemakkelijk optellen en aftrekken. (Denk aan dat recept!)
• Ze eenvoudig met elkaar vergelijken om te zien welke groter is. (Handig bij financiën!)
• Breuken beter begrijpen en ermee werken in complexere wiskundige problemen.

Eigenlijk is het een essentiële stap in de wereld van de wiskunde. Het is de basis voor veel meer complexe bewerkingen.

Hoe Maak Je Breuken Gelijknamig? De Stappen

Oké, laten we aan de slag gaan. Er zijn een paar methoden om breuken gelijknamig te maken. De meest gebruikte methode is het vinden van het kleinste gemene veelvoud (KGV) van de noemers. Dit is het kleinste getal dat door beide noemers gedeeld kan worden. Laten we dit stap voor stap bekijken:

Stap 1: Vind het Kleinste Gemene Veelvoud (KGV)

De KGV vinden is de cruciale eerste stap. Er zijn verschillende manieren om de KGV te vinden. Hier zijn er een paar:

• Methode 1: De Vermenigvuldigingslijst
  Schrijf de vermenigvuldigingslijst van beide noemers op, totdat je een getal vindt dat in beide lijsten voorkomt. Het kleinste getal dat in beide lijsten staat, is de KGV.

  Voorbeeld: Stel, we willen 1/4 en 1/6 gelijknamig maken. De noemers zijn 4 en 6.

  • Vermenigvuldigingslijst van 4: 4, 8, 12, 16, 20...
  • Vermenigvuldigingslijst van 6: 6, 12, 18, 24, 30...

  De KGV van 4 en 6 is dus 12.

• Methode 2: Priemfactoren ontbinden
  Ontbind beide noemers in priemfactoren. Neem vervolgens van elke priemfactor het hoogste aantal keren dat deze voorkomt in de ontbinding van een van de noemers. Vermenigvuldig deze priemfactoren met elkaar.

  Voorbeeld: Nogmaals 1/4 en 1/6.

  • Priemfactoren van 4: 2 x 2 = 2²
  • Priemfactoren van 6: 2 x 3

  De hoogste macht van 2 is 2² en de hoogste macht van 3 is 3¹. De KGV is dan 2² x 3 = 4 x 3 = 12.

• Methode 3: De GGD-formule
  Gebruik de formule: KGV(a, b) = (a * b) / GGD(a, b), waarbij GGD de grootste gemene deler is.

  Voorbeeld: Nogmaals 1/4 en 1/6.

  De GGD van 4 en 6 is 2.

  KGV(4, 6) = (4 * 6) / 2 = 24 / 2 = 12

Stap 2: Maak de Breuken Gelijknamig

Nu je de KGV hebt gevonden, moet je elke breuk omzetten zodat de noemer gelijk is aan de KGV. Dit doe je door zowel de teller (het getal boven de streep) als de noemer met hetzelfde getal te vermenigvuldigen. Het getal waarmee je de noemer vermenigvuldigt, moet resulteren in de KGV.

Voorbeeld: We hadden 1/4 en 1/6 en we hebben gevonden dat de KGV 12 is.

• Om 1/4 om te zetten naar een breuk met noemer 12, moet je de noemer (4) vermenigvuldigen met 3 (want 4 x 3 = 12). Om de breuk gelijk te houden, moet je ook de teller (1) vermenigvuldigen met 3. Dus 1/4 wordt 3/12.
• Om 1/6 om te zetten naar een breuk met noemer 12, moet je de noemer (6) vermenigvuldigen met 2 (want 6 x 2 = 12). Om de breuk gelijk te houden, moet je ook de teller (1) vermenigvuldigen met 2. Dus 1/6 wordt 2/12.

Nu zijn 1/4 en 1/6 gelijknamig gemaakt en omgezet naar respectievelijk 3/12 en 2/12.

Voorbeelden en Toepassingen

Laten we een paar voorbeelden bekijken om het concept verder te verduidelijken:

• Voorbeeld 1: Maak 2/3 en 1/5 gelijknamig.
  De KGV van 3 en 5 is 15.
  2/3 = (2 x 5) / (3 x 5) = 10/15
  1/5 = (1 x 3) / (5 x 3) = 3/15
  Dus 2/3 en 1/5 worden 10/15 en 3/15.
• Voorbeeld 2: Maak 3/8 en 5/12 gelijknamig.
  De KGV van 8 en 12 is 24.
  3/8 = (3 x 3) / (8 x 3) = 9/24
  5/12 = (5 x 2) / (12 x 2) = 10/24
  Dus 3/8 en 5/12 worden 9/24 en 10/24.

Praktische Toepassingen:

• Koken: Zoals eerder genoemd, is het aanpassen van recepten een veel voorkomende toepassing. Stel dat een recept 1/3 kopje bloem en 1/4 kopje suiker vereist. Om te zien welke ingrediënt je meer gebruikt, moet je de breuken gelijknamig maken. 1/3 = 4/12 en 1/4 = 3/12. Je gebruikt dus meer bloem.
• Tijd: Stel, je besteedt 1/2 uur aan het reizen naar je werk en 2/5 uur aan het reizen naar huis. Hoeveel tijd besteed je in totaal aan reizen? Je moet 1/2 en 2/5 gelijknamig maken. 1/2 = 5/10 en 2/5 = 4/10. Je besteedt dus 5/10 + 4/10 = 9/10 uur aan reizen, wat gelijk staat aan 54 minuten.

Veelgemaakte Fouten en Hoe Je Ze Kunt Vermijden

Het gelijknamig maken van breuken lijkt misschien eenvoudig, maar er zijn een paar veelgemaakte fouten die je kunt vermijden:

• Vergeten de teller mee te vermenigvuldigen: Dit is de meest voorkomende fout. Als je de noemer met een bepaald getal vermenigvuldigt, moet je ook de teller met hetzelfde getal vermenigvuldigen om de waarde van de breuk te behouden.
• De KGV verkeerd berekenen: Een verkeerde KGV leidt tot incorrecte gelijknamige breuken. Controleer je berekeningen zorgvuldig.
• Vereenvoudigen vergeten: Soms kun je de uiteindelijke breuk vereenvoudigen. Bijvoorbeeld, als je 6/12 krijgt, kun je dit vereenvoudigen tot 1/2. Dit is niet altijd nodig, maar het kan handig zijn voor verder gebruik.

Tips en Trucs voor Succes

Hier zijn nog een paar tips en trucs om het gelijknamig maken van breuken gemakkelijker te maken:

• Oefening baart kunst: Hoe meer je oefent, hoe sneller en nauwkeuriger je wordt.
• Gebruik visuele hulpmiddelen: Teken cirkels of rechthoeken en verdeel ze in gelijke delen om breuken te visualiseren. Dit kan helpen om het concept beter te begrijpen.
• Online hulpmiddelen: Er zijn veel online tools en rekenmachines die je kunnen helpen bij het vinden van de KGV en het gelijknamig maken van breuken. Gebruik ze gerust om je antwoorden te controleren.
• Vraag om hulp: Als je er echt niet uitkomt, vraag dan je leraar, een vriend of een familielid om hulp. Soms kan een andere uitleg net het verschil maken.

Conclusie

Het gelijknamig maken van breuken is een essentiële vaardigheid die je veel kan helpen in het dagelijks leven en bij het leren van wiskunde. Door de stappen in dit artikel te volgen en de tips en trucs toe te passen, zul je merken dat het helemaal niet zo moeilijk is als je dacht. Blijf oefenen en je zult er steeds beter in worden! En vergeet niet: iedereen maakt fouten, dus wees niet ontmoedigd als het niet meteen lukt. Het belangrijkste is dat je blijft leren en groeien.