Hoe Maak Je Een Boxplot

Heb je ooit data gezien die je overweldigde? Een grote tabel vol getallen kan moeilijk te interpreteren zijn. Gelukkig is er een visuele manier om data samen te vatten en inzichtelijk te maken: de boxplot, ook wel snorrendoos genoemd. Dit artikel is speciaal geschreven voor iedereen die meer wil leren over boxplots, van studenten tot professionals die data-analyses uitvoeren. We gaan stap voor stap bekijken hoe je een boxplot maakt en leert interpreteren.

Wat is een Boxplot en Waarom Zou Je Er Een Maken?

Een boxplot is een grafische weergave van de verdeling van een dataset. Het laat in één oogopslag de mediaan, de kwartielen en eventuele uitbijters zien. Hier zijn enkele redenen waarom boxplots zo handig zijn:

Overzichtelijke samenvatting: Een boxplot geeft een compact overzicht van de belangrijkste kenmerken van een dataset.
Vergelijkingen maken: Het is gemakkelijk om verschillende datasets met elkaar te vergelijken door hun boxplots naast elkaar te zetten.
Uitbijters identificeren: Boxplots helpen om uitschieters (uitbijters) in de data te identificeren, die verder onderzoek vereisen.
Inzicht in de verdeling: Een boxplot geeft inzicht in de spreiding en symmetrie (of asymmetrie) van de data.

Kortom, een boxplot is een krachtig hulpmiddel om snel een goed beeld van je data te krijgen en belangrijke patronen te ontdekken. Het is veel efficiënter dan bijvoorbeeld een tabel met ruwe data bekijken.

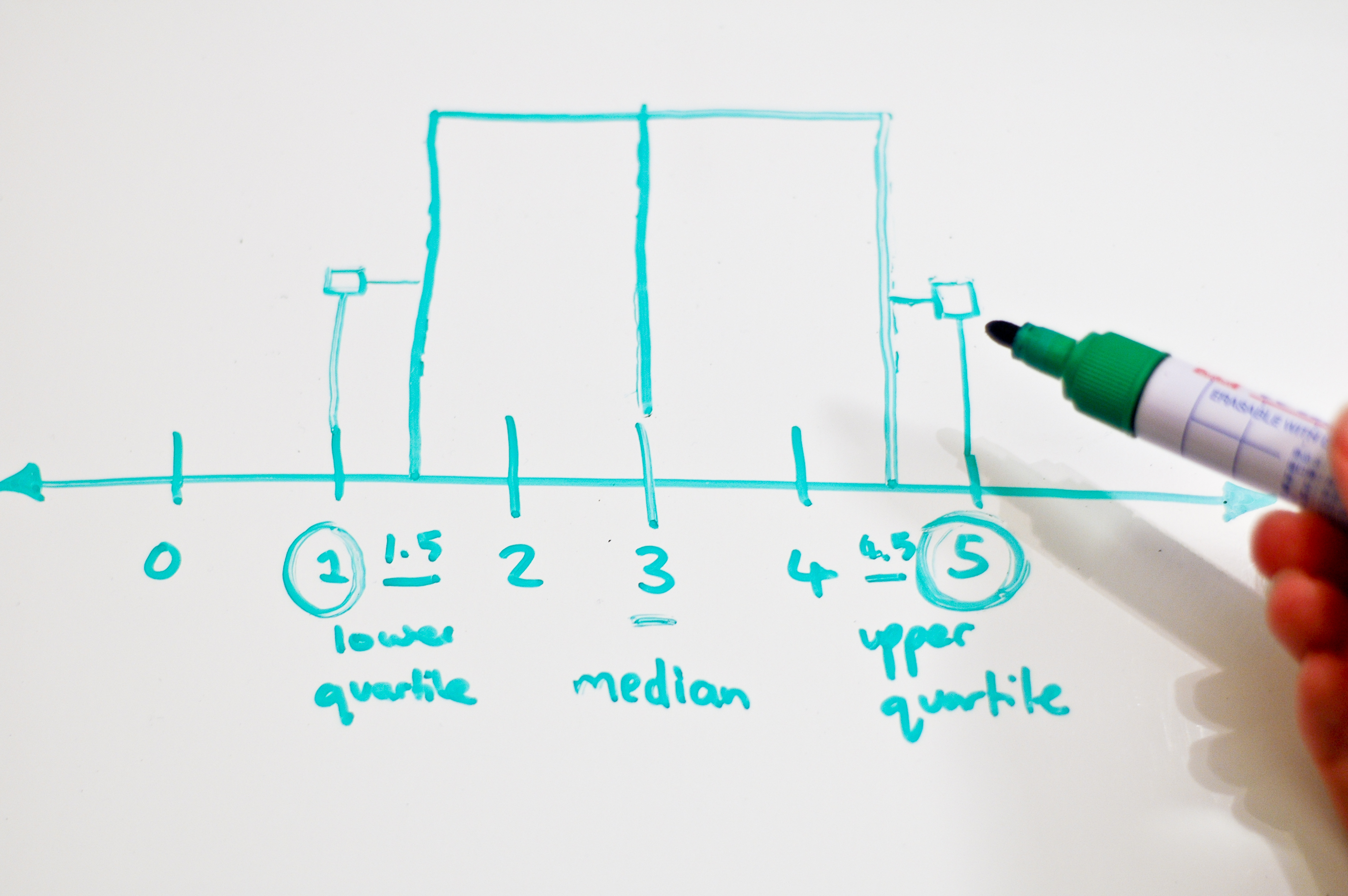
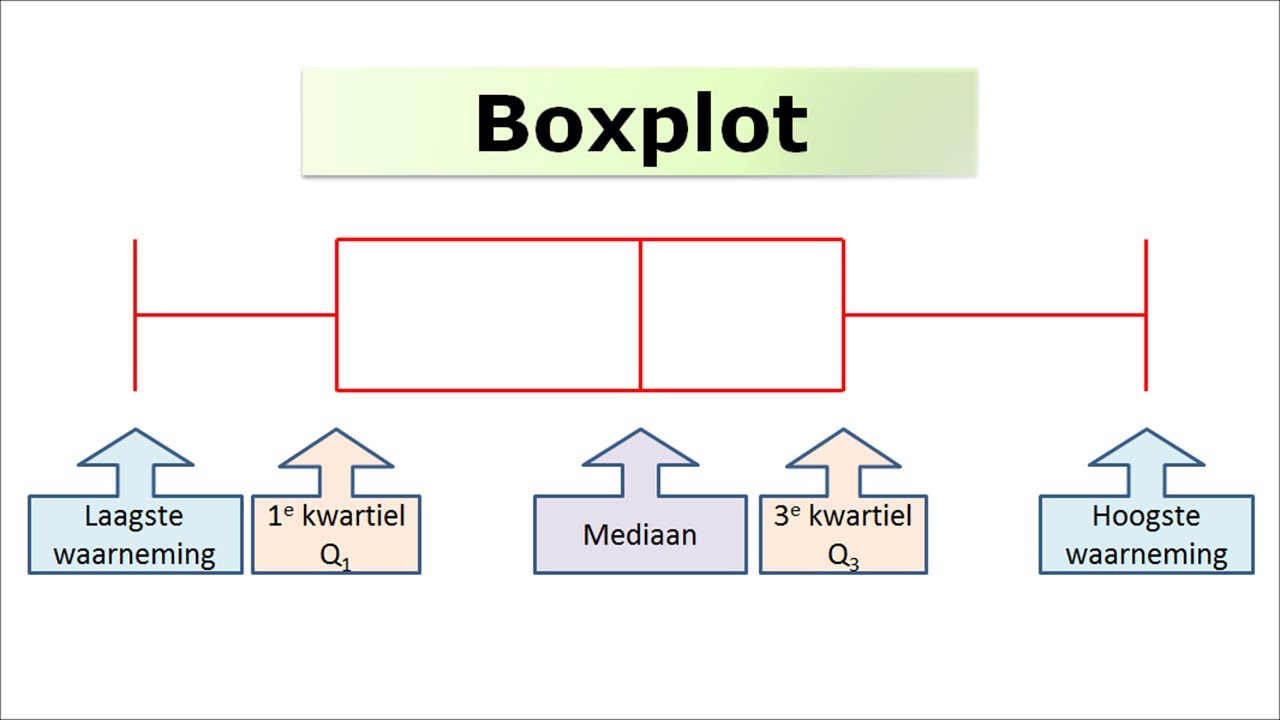
De Onderdelen van een Boxplot

Een boxplot bestaat uit de volgende onderdelen:

De Box: De box representeert het interkwartielbereik (IQR). De onderkant van de box is het eerste kwartiel (Q1), wat de 25e percentielwaarde is. De bovenkant van de box is het derde kwartiel (Q3), wat de 75e percentielwaarde is.
De Mediaanlijn: De lijn binnen de box geeft de mediaan (Q2) weer, wat de middelste waarde van de dataset is.
De Snorharen (Whiskers): De snorharen strekken zich uit vanaf de box tot aan de meest extreme datapunt binnen een bepaalde afstand. Meestal is deze afstand 1.5 keer de IQR (1.5 * (Q3 - Q1)).
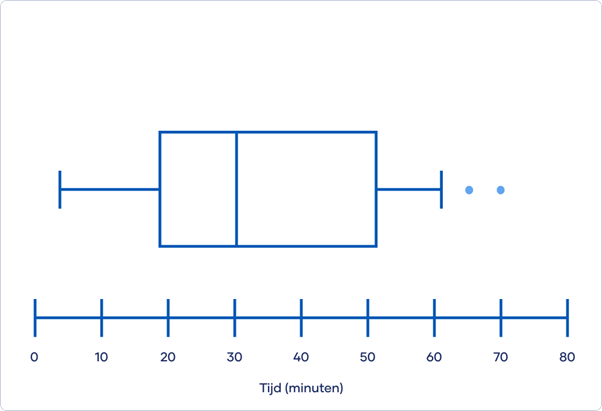
Uitbijters (Outliers): Punten die buiten de snorharen vallen, worden als uitbijters beschouwd en worden vaak individueel weergegeven als punten.

Het is belangrijk om deze onderdelen te begrijpen om de informatie uit een boxplot correct te kunnen interpreteren.

Hoe Maak Je Zelf Een Boxplot? (Stap voor Stap)

Laten we nu stap voor stap bekijken hoe je zelf een boxplot kunt maken. Je kunt dit handmatig doen, maar het is veel efficiënter om software te gebruiken.

Stap 1: Verzamel en Orden Je Data

De eerste stap is het verzamelen van de data die je wilt analyseren. Zorg ervoor dat de data schoon is en in een bruikbaar formaat staat, bijvoorbeeld in een spreadsheet (zoals Excel of Google Sheets) of een tabel in een database. Vervolgens is het handig om de data te ordenen, bijvoorbeeld van klein naar groot, om de kwartielen makkelijker te bepalen.

Voorbeeld: Stel, we hebben de volgende dataset met de lengte (in cm) van 10 studenten:

165, 170, 172, 175, 178, 180, 182, 185, 190, 200

Stap 2: Bereken de Kwartielen (Q1, Q2, Q3)

De volgende stap is het berekenen van de kwartielen:

Q2 (Mediaan): De mediaan is de middelste waarde. In dit geval zijn er 10 getallen, dus de mediaan is het gemiddelde van de 5e en 6e waarde: (178 + 180) / 2 = 179 cm.
Q1 (Eerste Kwartiel): Het eerste kwartiel is de mediaan van de waarden *onder* de algemene mediaan. In dit geval is dat: 165, 170, 172, 175, 178. De mediaan hiervan is 172 cm.
Q3 (Derde Kwartiel): Het derde kwartiel is de mediaan van de waarden *boven* de algemene mediaan. In dit geval is dat: 180, 182, 185, 190, 200. De mediaan hiervan is 185 cm.

Stap 3: Bereken het Interkwartielbereik (IQR)

Het interkwartielbereik (IQR) is het verschil tussen het derde en eerste kwartiel:

IQR = Q3 - Q1 = 185 cm - 172 cm = 13 cm

Stap 4: Bepaal de Grenzen voor Uitbijters

Om te bepalen welke waarden als uitbijters worden beschouwd, berekenen we de volgende grenzen:

Ondergrens: Q1 - (1.5 * IQR) = 172 cm - (1.5 * 13 cm) = 152.5 cm
Bovengrens: Q3 + (1.5 * IQR) = 185 cm + (1.5 * 13 cm) = 204.5 cm

Elke waarde die lager is dan 152.5 cm of hoger dan 204.5 cm wordt als een uitbijter beschouwd.

Stap 5: Teken de Boxplot

Nu kunnen we de boxplot tekenen:

Teken een verticale lijn met een schaal die de waarden in je dataset omvat.
Teken de box met de onderkant op Q1 (172 cm) en de bovenkant op Q3 (185 cm).
Teken een lijn binnen de box op de mediaan (179 cm).
Teken de snorharen. De snorharen strekken zich uit tot de laagste en hoogste waarden die *niet* als uitbijter worden beschouwd. In dit geval is de laagste waarde 165 cm en de hoogste waarde 190 cm (de waarde 200cm is een uitbijter).
Markeer de uitbijters. In dit geval is de waarde 200 cm een uitbijter, omdat deze boven de bovengrens van 204.5 cm ligt. Teken dit als een punt boven de snorhaar.

Hoewel je dit handmatig kunt doen, is het veel gebruikelijker en efficiënter om software te gebruiken.

Boxplots Maken met Software

Er zijn verschillende softwarepakketten beschikbaar waarmee je gemakkelijk boxplots kunt maken:

Excel: Excel heeft een ingebouwde functie om boxplots te maken. Selecteer je data, ga naar "Insert" -> "Chart" en kies de "Box and Whisker" chart.
Google Sheets: Google Sheets biedt ook de mogelijkheid om boxplots te maken. De stappen zijn vergelijkbaar met Excel.
R: R is een programmeertaal die veel gebruikt wordt voor statistische analyses. Met de `boxplot()` functie kun je eenvoudig boxplots genereren.
Python (met Matplotlib of Seaborn): Python is een andere populaire programmeertaal voor data-analyse. De bibliotheken Matplotlib en Seaborn bieden functies om boxplots te maken.
SPSS: SPSS is een statistisch softwarepakket dat veel gebruikt wordt in de sociale wetenschappen. Het heeft uitgebreide mogelijkheden voor het maken van boxplots en andere grafieken.

Het gebruik van software maakt het proces veel sneller en nauwkeuriger, vooral bij grote datasets. Bovendien bieden deze tools vaak extra opties voor het aanpassen van de boxplot, zoals het toevoegen van labels en het veranderen van de kleuren.

Boxplots Interpreteren: Wat Kun Je Eruit Halen?

Nu je weet hoe je een boxplot maakt, is het belangrijk om te leren hoe je hem moet interpreteren. Hier zijn enkele belangrijke aspecten:

De Mediaan: De positie van de mediaanlijn binnen de box geeft aan of de data symmetrisch verdeeld is. Als de mediaan in het midden van de box ligt, is de verdeling ongeveer symmetrisch. Als de mediaan meer naar de onderkant van de box verschoven is, is de verdeling rechtsscheef (positief scheef), en als de mediaan meer naar de bovenkant van de box verschoven is, is de verdeling linksscheef (negatief scheef).
De Spreiding: De lengte van de box (IQR) geeft aan hoe groot de spreiding van de middelste 50% van de data is. Een lange box betekent een grotere spreiding, terwijl een korte box een kleinere spreiding betekent.
De Snorharen: De lengte van de snorharen geeft aan hoe de rest van de data verdeeld is. Lange snorharen duiden op een grotere spreiding in de staarten van de verdeling, terwijl korte snorharen duiden op een kleinere spreiding.
De Uitbijters: Uitbijters kunnen indicaties geven van ongewone waarden of fouten in de data. Het is belangrijk om uitbijters nader te onderzoeken om te bepalen of ze valide zijn of dat ze verwijderd moeten worden.

Door deze aspecten te analyseren, kun je een goed beeld krijgen van de verdeling van de data en belangrijke patronen ontdekken. Vergeet niet om altijd de context van de data in overweging te nemen bij het interpreteren van een boxplot.

Voorbeeld Interpretatie

Stel, we hebben een boxplot van de salarissen van werknemers in een bedrijf. We zien dat de mediaanlijn dicht bij de bovenkant van de box ligt en dat er enkele uitbijters aan de bovenkant zijn. Dit kan erop wijzen dat de salarissen rechtsscheef verdeeld zijn (de meeste werknemers verdienen minder dan het gemiddelde) en dat er enkele werknemers zijn met zeer hoge salarissen.

Tips en Trucs voor Effectieve Boxplots

Hier zijn enkele tips en trucs om je boxplots nog effectiever te maken:

Gebruik labels: Zorg ervoor dat je boxplot duidelijke labels heeft voor de assen en de verschillende groepen data.
Gebruik kleuren: Kleuren kunnen helpen om verschillende groepen data te onderscheiden.
Vergelijk meerdere boxplots: Zet meerdere boxplots naast elkaar om verschillende datasets met elkaar te vergelijken.
Combineer met andere grafieken: Combineer boxplots met andere grafieken, zoals histogrammen of spreidingsdiagrammen, om een completer beeld van de data te krijgen.
Wees voorzichtig met de schaal: Zorg ervoor dat de schaal van de assen geschikt is voor de data. Een verkeerde schaal kan de boxplot misleidend maken.

Door deze tips toe te passen, kun je ervoor zorgen dat je boxplots duidelijk, informatief en effectief zijn.

Conclusie

De boxplot is een krachtig en veelzijdig hulpmiddel voor het visualiseren en samenvatten van data. Door de onderdelen van een boxplot te begrijpen en te weten hoe je er een maakt en interpreteert, kun je snel en gemakkelijk inzicht krijgen in de verdeling van je data en belangrijke patronen ontdekken. Of je nu een student bent die data-analyse leert of een professional die dagelijks met data werkt, de boxplot is een waardevolle tool die je in je arsenaal zou moeten hebben. Experimenteer met verschillende datasets en softwarepakketten om je vaardigheden verder te ontwikkelen en de kracht van boxplots volledig te benutten! Hopelijk heeft dit artikel je de nodige kennis en inspiratie gegeven om zelf aan de slag te gaan.