Hoe Reken Je Met Breuken
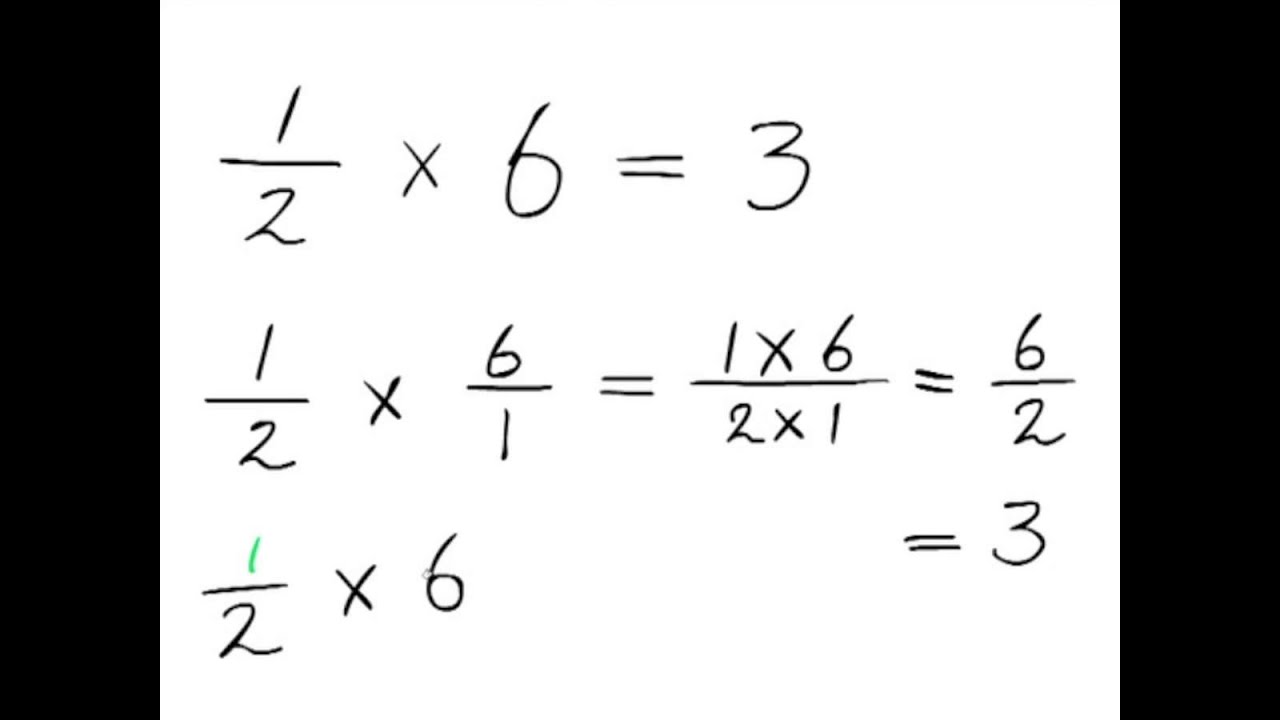
Ken je dat? Je staat in de keuken, wilt een taart bakken, en het recept vraagt om ⅓ kopje bloem. Maar je hebt alleen maatbekers voor ¼ kopje en ½ kopje. Paniek! Rekenen met breuken kan soms voelen als een heuse uitdaging. Je bent zeker niet de enige. Veel mensen vinden breuken lastig, en dat is helemaal oké. Het goede nieuws is: met de juiste uitleg en wat oefening, kun je het leren!
Deze artikel is er om je stap voor stap door de wereld van breuken te loodsen. We gaan samen bekijken wat breuken precies zijn, hoe je ze optelt, aftrekt, vermenigvuldigt en deelt. Klaar om de controle over breuken te krijgen?
Wat is een Breuk Eigenlijk?
Laten we beginnen bij de basis. Een breuk is niets meer dan een deel van een geheel. Denk aan een pizza. Als je de pizza in acht stukken snijdt en er één stuk van neemt, dan heb je ⅛ van de pizza. Die ⅛, dat is een breuk.
Een breuk bestaat uit twee getallen, gescheiden door een streep:
- De teller (het getal boven de streep): Dit getal geeft aan hoeveel delen je hebt. In het voorbeeld van de pizza is de teller 1 (één stuk).
- De noemer (het getal onder de streep): Dit getal geeft aan in hoeveel gelijke delen het geheel verdeeld is. In het pizza voorbeeld is de noemer 8 (acht stukken).
Dus, ⅛ betekent "één van de acht gelijke delen". Makkelijk, toch?
Breuken Vereenvoudigen: Maak Het Simpeler!
Soms kun je breuken vereenvoudigen, ook wel "korter schrijven" genoemd. Dit betekent dat je de breuk kleiner maakt, maar de waarde hetzelfde blijft. Denk aan de breuk 2/4. Dit betekent "twee van de vier gelijke delen". Maar je kunt het ook zien als "de helft". Dus, 2/4 is hetzelfde als ½.
Hoe vereenvoudig je een breuk? Je zoekt naar het grootste getal waardoor zowel de teller als de noemer deelbaar zijn. Dit getal noem je de grootste gemene deler (GGD). In het geval van 2/4 is de GGD 2. Je deelt zowel de teller als de noemer door 2: 2 ÷ 2 = 1 en 4 ÷ 2 = 2. Dus, 2/4 vereenvoudigt tot ½.
Voorbeeld: Vereenvoudig de breuk 6/12.
- De GGD van 6 en 12 is 6.
- Deel de teller en de noemer door 6: 6 ÷ 6 = 1 en 12 ÷ 6 = 2.
- Dus, 6/12 vereenvoudigt tot ½.
Breuken Optellen en Aftrekken: Gelijke Noemers Zijn Essentieel!
Om breuken op te tellen of af te trekken, moeten ze eerst dezelfde noemer hebben. Dit betekent dat de breuken verdeeld moeten zijn in even grote stukken. Stel je voor: je wilt ½ pizza optellen bij ¼ pizza. Dat gaat niet zomaar, want de stukken zijn niet even groot.
Om de noemers gelijk te maken, zoek je naar een gemeenschappelijke noemer. Vaak is de eenvoudigste manier om de noemers van beide breuken te vermenigvuldigen. Maar soms is er een kleinere gemeenschappelijke noemer mogelijk (het kleinste gemene veelvoud, KGV).
Voorbeeld: Tel ½ en ¼ bij elkaar op.
- De noemers zijn 2 en 4.
- Een gemeenschappelijke noemer is 4 (omdat 2 x 2 = 4).
- Maak de breuken gelijknamig: ½ wordt 2/4 (vermenigvuldig de teller en de noemer van ½ met 2).
- Nu kun je optellen: 2/4 + ¼ = 3/4.
Aftrekken werkt op dezelfde manier: zorg voor gelijke noemers en trek dan de tellers van elkaar af.
Voorbeeld: Bereken ⅔ - ¼
- De noemers zijn 3 en 4.
- De KGV van 3 en 4 is 12.
- Maak de breuken gelijknamig: ⅔ wordt 8/12 (vermenigvuldig teller en noemer met 4) en ¼ wordt 3/12 (vermenigvuldig teller en noemer met 3).
- Nu kun je aftrekken: 8/12 - 3/12 = 5/12.
Breuken Vermenigvuldigen: Eenvoudiger dan Je Denkt!
Breuken vermenigvuldigen is eigenlijk heel simpel. Je vermenigvuldigt gewoon de tellers met elkaar en de noemers met elkaar.
Voorbeeld: Bereken ½ x ⅓.
- Vermenigvuldig de tellers: 1 x 1 = 1.
- Vermenigvuldig de noemers: 2 x 3 = 6.
- Dus, ½ x ⅓ = ⅙.
Soms kun je de uitkomst nog vereenvoudigen, zoals we eerder hebben geleerd.
Breuken Delen: Omkeren en Vermenigvuldigen!
Breuken delen lijkt misschien ingewikkeld, maar er is een handige truc: je keert de tweede breuk om (verwisselt de teller en de noemer) en vermenigvuldigt vervolgens de breuken.
Voorbeeld: Bereken ½ : ¼.
- Keer de tweede breuk om: ¼ wordt 4/1.
- Vermenigvuldig de breuken: ½ x 4/1 = 4/2.
- Vereenvoudig de breuk: 4/2 = 2.
- Dus, ½ : ¼ = 2.
Waarom werkt dit? Delen is eigenlijk het tegenovergestelde van vermenigvuldigen. Door de breuk om te keren, maak je van de deling een vermenigvuldiging met de inverse.
Gemengde Getallen: Hele Getallen en Breuken
Een gemengd getal bestaat uit een heel getal en een breuk, bijvoorbeeld 2 ½. Soms is het handig om een gemengd getal om te zetten naar een onechte breuk (een breuk waarbij de teller groter is dan de noemer) en vice versa.
Gemengd getal omzetten naar een onechte breuk:
- Vermenigvuldig het hele getal met de noemer van de breuk.
- Tel de teller van de breuk bij de uitkomst op.
- Zet het resultaat boven de oorspronkelijke noemer.
Voorbeeld: Zet 2 ½ om naar een onechte breuk.
- Vermenigvuldig het hele getal met de noemer: 2 x 2 = 4.
- Tel de teller erbij op: 4 + 1 = 5.
- Zet het resultaat boven de noemer: 5/2.
- Dus, 2 ½ = 5/2.
Onechte breuk omzetten naar een gemengd getal:
- Deel de teller door de noemer.
- Het quotiënt is het hele getal.
- De rest is de teller van de breuk. De noemer blijft hetzelfde.
Voorbeeld: Zet 7/3 om naar een gemengd getal.
- Deel de teller door de noemer: 7 ÷ 3 = 2 met een rest van 1.
- Het hele getal is 2.
- De teller van de breuk is 1. De noemer blijft 3.
- Dus, 7/3 = 2 ⅓.
Tips & Tricks voor het Rekenen met Breuken
- Oefening baart kunst! Hoe meer je oefent, hoe beter je wordt in het rekenen met breuken.
- Gebruik visuals: Teken cirkels of rechthoeken en verdeel ze in stukken om breuken te visualiseren.
- Begin simpel: Start met eenvoudige breuken en ga geleidelijk over naar moeilijkere opgaven.
- Vraag om hulp: Schaam je niet om hulp te vragen aan een leraar, vriend of familielid.
- Gebruik online tools: Er zijn veel online rekenmachines en oefeningen beschikbaar om je te helpen.
- Herken breuken in het dagelijks leven: Let op breuken in recepten, klokkijken, en andere situaties.
- Wees geduldig: Het kost tijd om breuken onder de knie te krijgen. Geef niet op!
Conclusie
Rekenen met breuken hoeft geen onoverkomelijk probleem te zijn. Met een beetje uitleg, oefening en geduld, kun je de basisprincipes onder de knie krijgen en je zelfverzekerder voelen bij het oplossen van breukenproblemen. Onthoud: breuken zijn overal om ons heen. Van het verdelen van een pizza tot het berekenen van de juiste hoeveelheid ingrediënten voor een recept. Dus, pak die breuken aan, oefen en je zult zien: het wordt steeds makkelijker!
Hopelijk heeft deze gids je geholpen om een beter begrip van breuken te krijgen. Succes met oefenen!
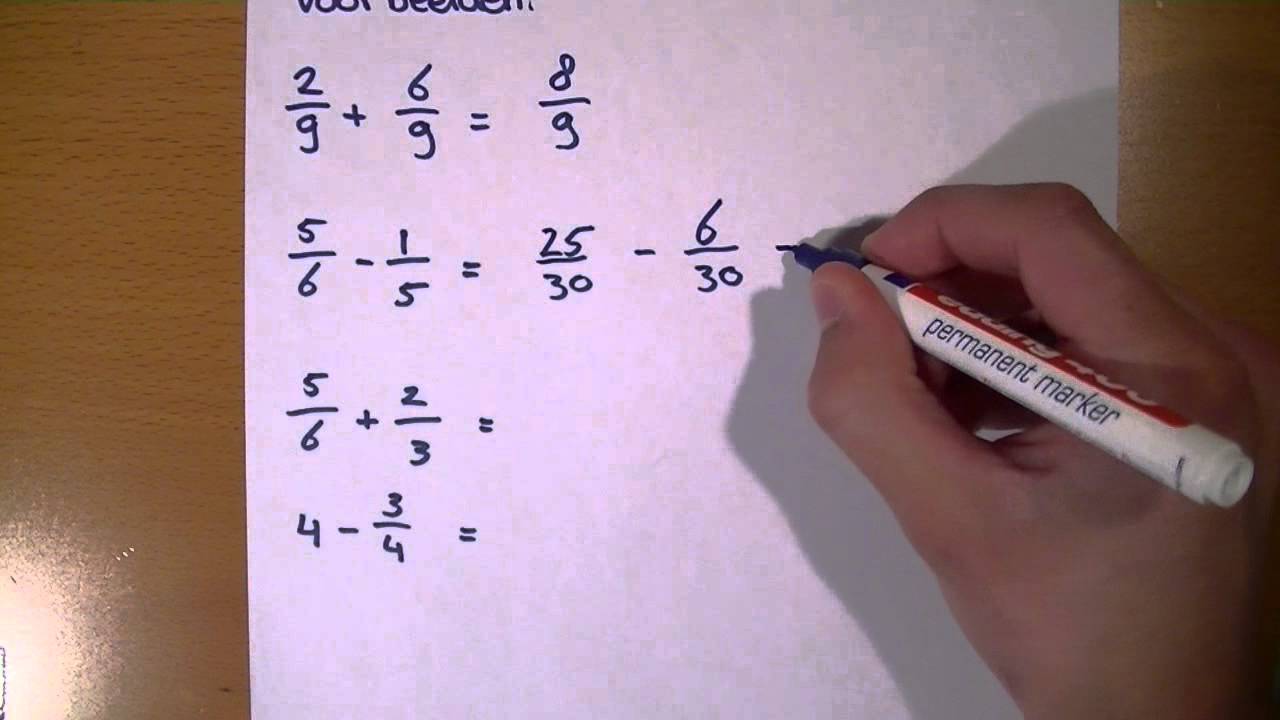
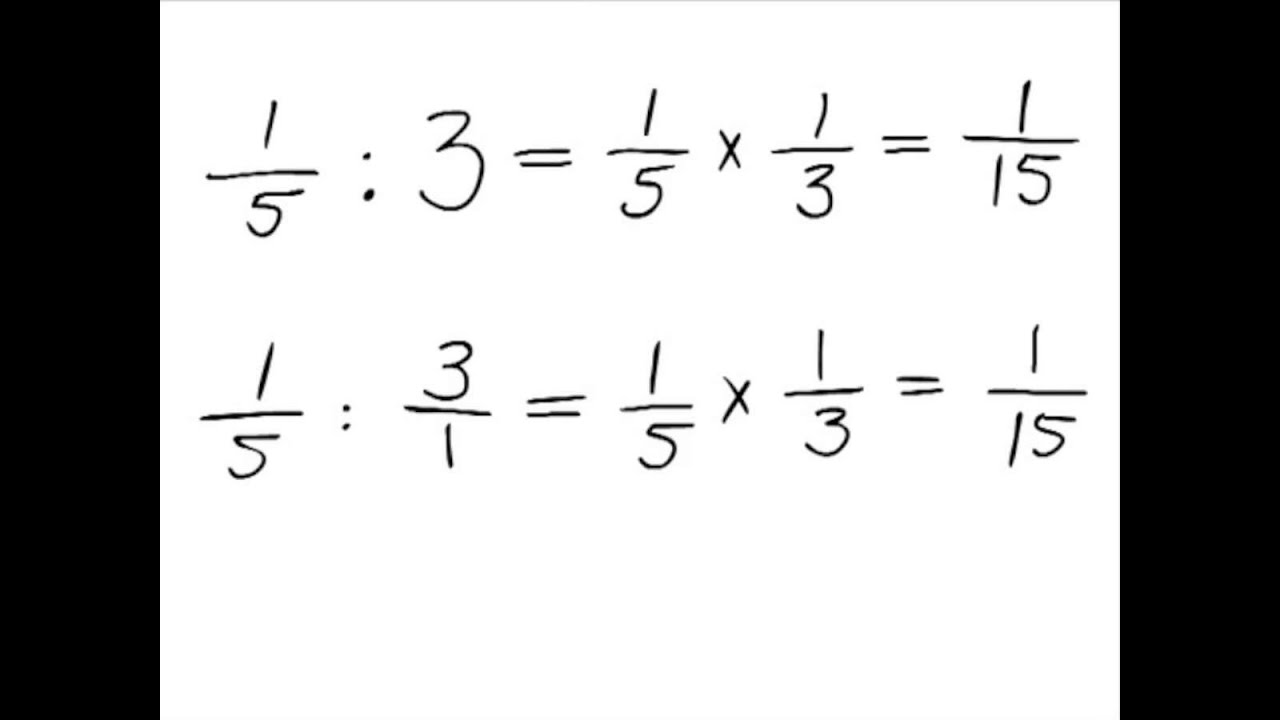
Bekijk ook deze gerelateerde berichten:
- Kan Je Wiskunde Laten Vallen Op Havo
- Hoeveel Erfbelasting Moet Ik Betalen
- Hoe Lang Is Herpes Besmettelijk
- Hoeveel Mensen Slagen De Eerste Keer Rijexamen
- Hoeveel Vaste Voeding Baby 6 Maanden
- Wat Was Was Voor Was Was Was
- Wat Is De Straal Van De Aarde
- De Dichter Is Het Hart Van De Wereld
- Hoeveel Eenheden Insuline Per Keer
- Hoe Warm Is Het In De Woestijn
