Hoe Teken Je Een Boxplot

Heb je ooit naar een dataset gekeken en gedacht: "Waar moet ik in vredesnaam beginnen?" Dat is heel normaal! Data kan overweldigend zijn, en het begrijpen van de verdeling ervan kan een flinke uitdaging zijn. Maar wat als ik je zou vertellen dat er een visuele tool is die je in één oogopslag cruciale inzichten kan geven? Maak kennis met de boxplot, ook wel bekend als de snorrendoos!

Dit artikel is jouw gids om te leren hoe je zelf een boxplot tekent. We gaan het simpel houden, zonder ingewikkelde statistische termen. We focussen op de praktische stappen en laten je zien hoe je met een paar eenvoudige berekeningen een krachtig visueel overzicht van je data kunt maken. Dus, pak een pen en papier (of je favoriete spreadsheetprogramma) en laten we beginnen!

Wat is een Boxplot en Waarom Zou Je Er Eentje Tekenen?

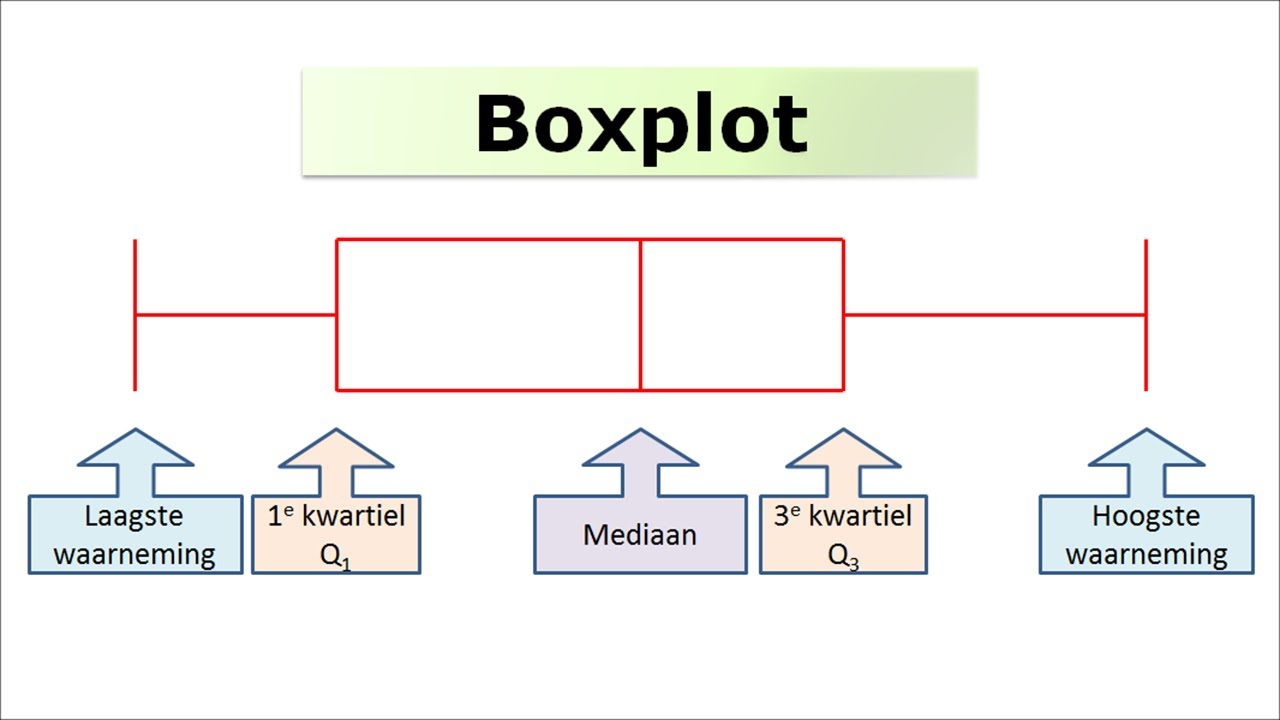
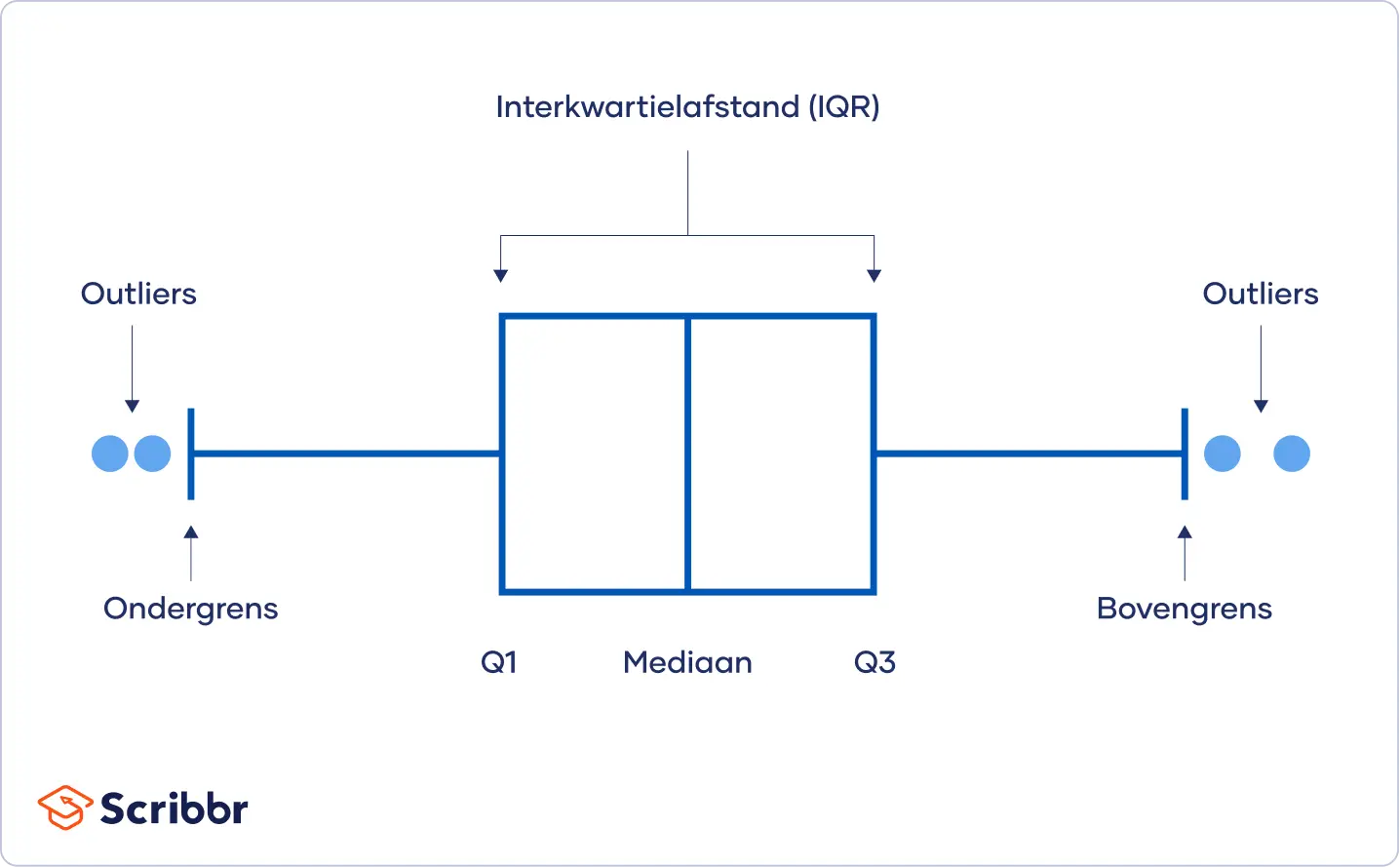
Een boxplot is een gestandaardiseerde manier om de verdeling van een dataset weer te geven op basis van vijf belangrijke getallen: het minimum, het eerste kwartiel (Q1), de mediaan (Q2), het derde kwartiel (Q3), en het maximum. De "box" zelf vertegenwoordigt het interkwartielbereik (IQR), wat het verschil is tussen Q3 en Q1. De "snorren" strekken zich uit van de box tot de minimale en maximale waarden, binnen een bepaalde range. Alles wat daarbuiten valt, wordt beschouwd als een uitbijter.

Waarom zou je dit allemaal willen weten? Omdat een boxplot je helpt om:

De centrale tendentie te zien: De mediaan geeft je een idee van het midden van de data.
De spreiding te beoordelen: De breedte van de box en de lengte van de snorren laten zien hoe gevarieerd de data is.
Uitschieters te identificeren: Punten buiten de snorren zijn potentiële uitschieters die verder onderzoek waard zijn.
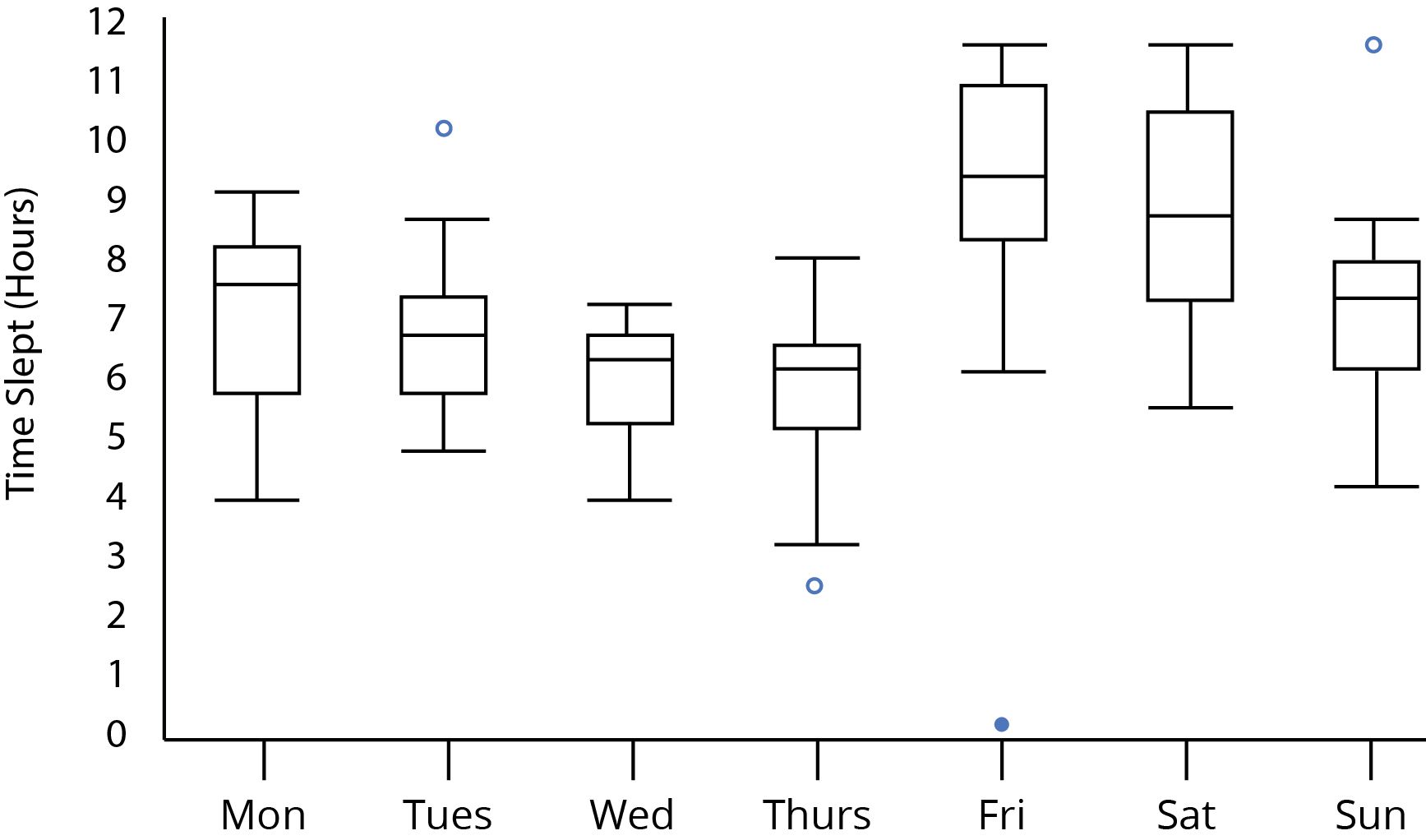
Verdelingen te vergelijken: Je kunt gemakkelijk boxplots van verschillende datasets naast elkaar zetten om ze te vergelijken.

Denk bijvoorbeeld aan salarisgegevens van twee verschillende bedrijven. Door boxplots te tekenen, kun je snel zien welk bedrijf een hoger mediaansalaris heeft, welke grotere salarisverschillen kent en of er uitschieters zijn (bijvoorbeeld extreem hoge salarissen van directieleden).

Stap-voor-Stap: Hoe Teken Je een Boxplot

Nu gaan we aan de slag met het tekenen van een boxplot. We gebruiken een fictieve dataset van 20 scores op een wiskunde toets:

45, 52, 55, 60, 62, 65, 68, 70, 72, 75, 78, 80, 82, 85, 88, 90, 92, 95, 98, 100

Stap 1: Sorteer de Data

De eerste stap is cruciaal: sorteer de data van laag naar hoog. Dit maakt het veel gemakkelijker om de kwartielen te vinden. In ons voorbeeld is de data al gesorteerd, dus we kunnen meteen door.

Stap 2: Bepaal de Mediaan (Q2)

De mediaan is de middelste waarde van de dataset. Omdat we een even aantal (20) scores hebben, is de mediaan het gemiddelde van de 10e en 11e score. In dit geval is dat (75 + 78) / 2 = 76.5. Dit is onze Q2.

Stap 3: Bepaal het Eerste Kwartiel (Q1)

Het eerste kwartiel is de mediaan van de data onder de mediaan. We kijken dus naar de scores 45 tot en met 75. Er zijn 10 scores, dus de mediaan is het gemiddelde van de 5e en 6e score: (62 + 65) / 2 = 63.5. Dit is onze Q1.

Stap 4: Bepaal het Derde Kwartiel (Q3)

Het derde kwartiel is de mediaan van de data boven de mediaan. We kijken dus naar de scores 78 tot en met 100. Ook hier zijn 10 scores, dus de mediaan is het gemiddelde van de 5e en 6e score in deze subset: (88 + 90) / 2 = 89. Dit is onze Q3.

Stap 5: Bepaal het Minimum en Maximum

Dit is makkelijk! Het minimum is de laagste score in de dataset: 45. Het maximum is de hoogste score in de dataset: 100.

Stap 6: Bereken het Interkwartielbereik (IQR)

Het IQR is het verschil tussen Q3 en Q1: IQR = Q3 - Q1 = 89 - 63.5 = 25.5. De IQR is belangrijk voor het bepalen van uitschieters.

Stap 7: Bepaal de Grenswaarden voor Uitschieters

Om uitschieters te identificeren, berekenen we de volgende grenswaarden:

Ondergrens: Q1 - 1.5 * IQR = 63.5 - 1.5 * 25.5 = 25.25
Bovengrens: Q3 + 1.5 * IQR = 89 + 1.5 * 25.5 = 127.25

Elke waarde die lager is dan 25.25 of hoger dan 127.25 wordt beschouwd als een potentiële uitschieter.

Stap 8: Teken de Boxplot

Nu kunnen we eindelijk de boxplot tekenen!

Teken een getallenlijn: Zorg ervoor dat de getallenlijn de hele range van je data omvat, inclusief de onder- en bovengrens voor uitschieters.
Teken de Box: Teken een rechthoekige box die loopt van Q1 (63.5) tot Q3 (89).
Teken de Mediaan: Trek een verticale lijn door de box op de positie van de mediaan (76.5).
Teken de Snorren: De snorren lopen van de box tot de laagste en hoogste waarden binnen de grenswaarden voor uitschieters. In ons geval is de laagste waarde binnen de ondergrens 45. De hoogste waarde binnen de bovengrens is 100. Dus de snorren lopen van 63.5 naar 45 en van 89 naar 100.
Teken Uitschieters: Als er waarden buiten de snorren vallen (buiten de grenswaarden), teken ze dan als individuele punten. In ons voorbeeld hebben we geen uitschieters, omdat alle data tussen 45 en 100 ligt, en dus binnen de berekende grenswaarden.

En voilà! Je hebt je eigen boxplot getekend! Het geeft je in één oogopslag een overzicht van de verdeling van de wiskundetoetsscores.

Alternatieven voor Handmatig Tekenen

Hoewel het handmatig tekenen van een boxplot nuttig is om het concept te begrijpen, zijn er natuurlijk veel handigere manieren om dit te doen, vooral als je met grote datasets werkt. Hier zijn een paar populaire opties:

Spreadsheetprogramma's (Excel, Google Sheets): De meeste spreadsheetprogramma's hebben ingebouwde functies om boxplots te maken. Selecteer je data, kies de optie om een diagram te maken en selecteer "boxplot".
Statistische Software (R, SPSS, Python met Matplotlib of Seaborn): Deze tools bieden meer flexibiliteit en controle over de vormgeving van je boxplots. Ze zijn vooral handig voor complexere analyses.
Online Boxplot Generators: Er zijn verschillende websites waar je je data kunt plakken en direct een boxplot kunt genereren.

Welke methode je ook kiest, de principes blijven hetzelfde: je wilt de mediaan, kwartielen, minimum, maximum en eventuele uitschieters visueel weergeven om inzicht te krijgen in de verdeling van je data.

Tips voor het Interpreteren van Boxplots

Nu je weet hoe je een boxplot tekent (of genereert), is het belangrijk om te begrijpen hoe je hem moet interpreteren:

Symmetrische verdeling: Als de mediaan in het midden van de box ligt en de snorren ongeveer even lang zijn, is de data redelijk symmetrisch verdeeld.
Scheve verdeling (rechts): Als de mediaan dichter bij Q1 ligt en de snor naar rechts langer is, is de data rechts scheef (positief scheef). Dit betekent dat er meer waarden aan de lage kant zijn en een paar zeer hoge waarden.
Scheve verdeling (links): Als de mediaan dichter bij Q3 ligt en de snor naar links langer is, is de data links scheef (negatief scheef). Dit betekent dat er meer waarden aan de hoge kant zijn en een paar zeer lage waarden.
Uitschieters: Wees alert op uitschieters. Ze kunnen wijzen op meetfouten, ongebruikelijke gebeurtenissen of gewoon extreme waarden. Onderzoek deze verder om te bepalen of ze relevant zijn voor je analyse.
Vergelijk Boxplots: Het echte nut van boxplots komt naar voren als je ze gebruikt om verschillende datasets te vergelijken. Kijk naar verschillen in mediaan, IQR en uitschieters om patronen en trends te ontdekken.

Voorbeeld: Stel dat je boxplots vergelijkt van de verkoopcijfers van twee verschillende producten. Als product A een hogere mediaan heeft dan product B, maar ook meer uitschieters aan de bovenkant, kan dit erop wijzen dat product A over het algemeen beter verkoopt, maar dat een paar individuele verkopen enorm succesvol zijn. Product B kan stabielere verkoopcijfers laten zien.

Conclusie

De boxplot is een krachtige en veelzijdige tool om data te visualiseren en te begrijpen. Het geeft je snel inzicht in de centrale tendentie, spreiding en uitschieters van je data. Door de stappen in dit artikel te volgen, kun je zelf boxplots tekenen en interpreteren, waardoor je een betere basis hebt voor data-analyse en besluitvorming. Of je nu een student bent, een onderzoeker, of gewoon iemand die nieuwsgierig is naar data, de boxplot is een waardevolle vaardigheid om te beheersen.

Dus, duik in je data, teken die boxplots, en ontdek de verborgen verhalen die ze te vertellen hebben!