Hoe Werkt De Stelling Van Pythagoras

Heb je je ooit afgevraagd hoe timmerlieden perfect rechthoekige hoeken maken zonder ingewikkelde apparatuur? Of hoe navigators afstanden over land of zee berekenen, zonder elke meter te hoeven meten? Het antwoord ligt in een fundamenteel, maar krachtig wiskundig principe: de Stelling van Pythagoras. Deze stelling is niet alleen voor wiskundigen; het is een praktische tool die in verrassend veel alledaagse situaties van toepassing is.

Dit artikel is speciaal geschreven voor jou, of je nu een student bent die worstelt met meetkunde, een ouder die je kind helpt met huiswerk, of gewoon iemand die geïnteresseerd is in hoe wiskunde de wereld om ons heen vormgeeft. We zullen de Stelling van Pythagoras op een duidelijke en toegankelijke manier uitleggen, illustraties geven en laten zien hoe je deze in de praktijk kunt gebruiken.

Wat is de Stelling van Pythagoras?

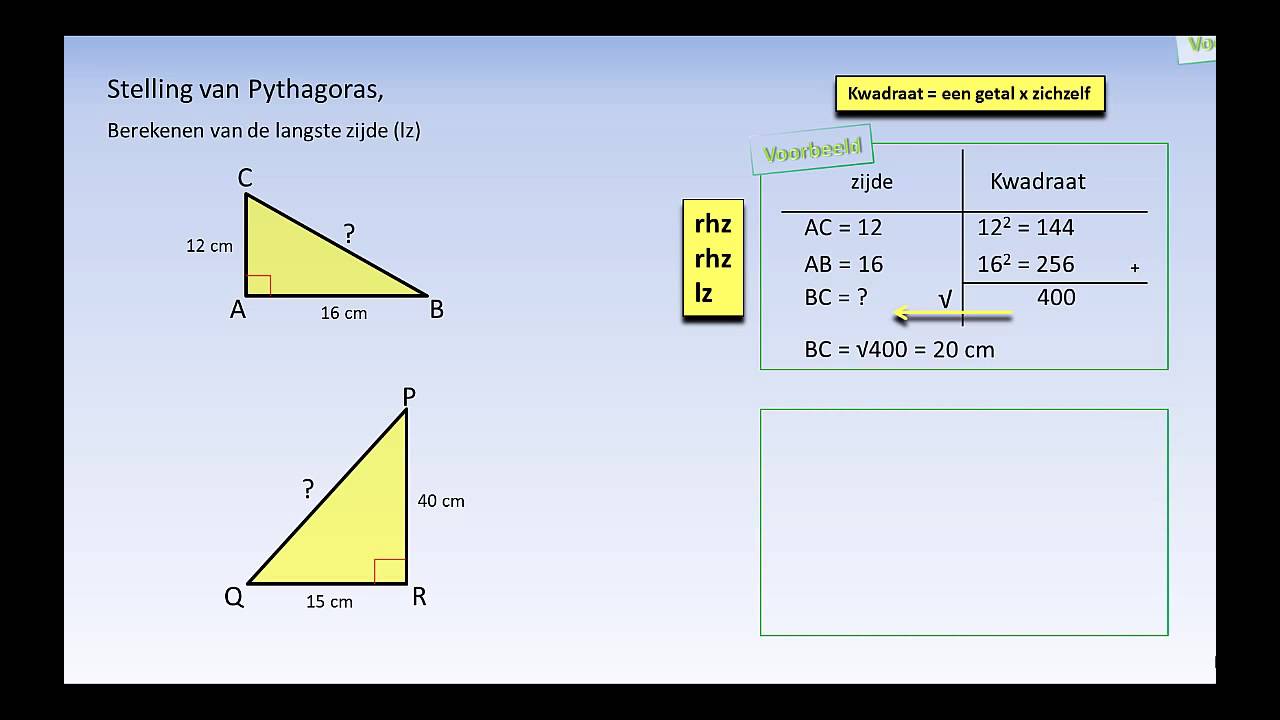
De Stelling van Pythagoras is een fundamentele relatie in de Euclidische meetkunde, die de zijden van een rechthoekige driehoek relateert. Een rechthoekige driehoek is een driehoek met één hoek van precies 90 graden (een rechte hoek). De zijde tegenover de rechte hoek wordt de hypotenusa genoemd, en de andere twee zijden worden de rechthoekszijden (of cathetus) genoemd.

De stelling, vernoemd naar de Griekse wiskundige Pythagoras (ca. 570 – ca. 495 v.Chr.), stelt dat:

In een rechthoekige driehoek is het kwadraat van de lengte van de hypotenusa (de zijde tegenover de rechte hoek) gelijk aan de som van de kwadraten van de lengtes van de twee andere zijden (de rechthoekszijden).

Wiskundig kunnen we dit als volgt uitdrukken:

a² + b² = c²

Waar:

a en b de lengtes van de rechthoekszijden zijn.
c de lengte van de hypotenusa is.

Een visueel bewijs: Waarom is dit waar?

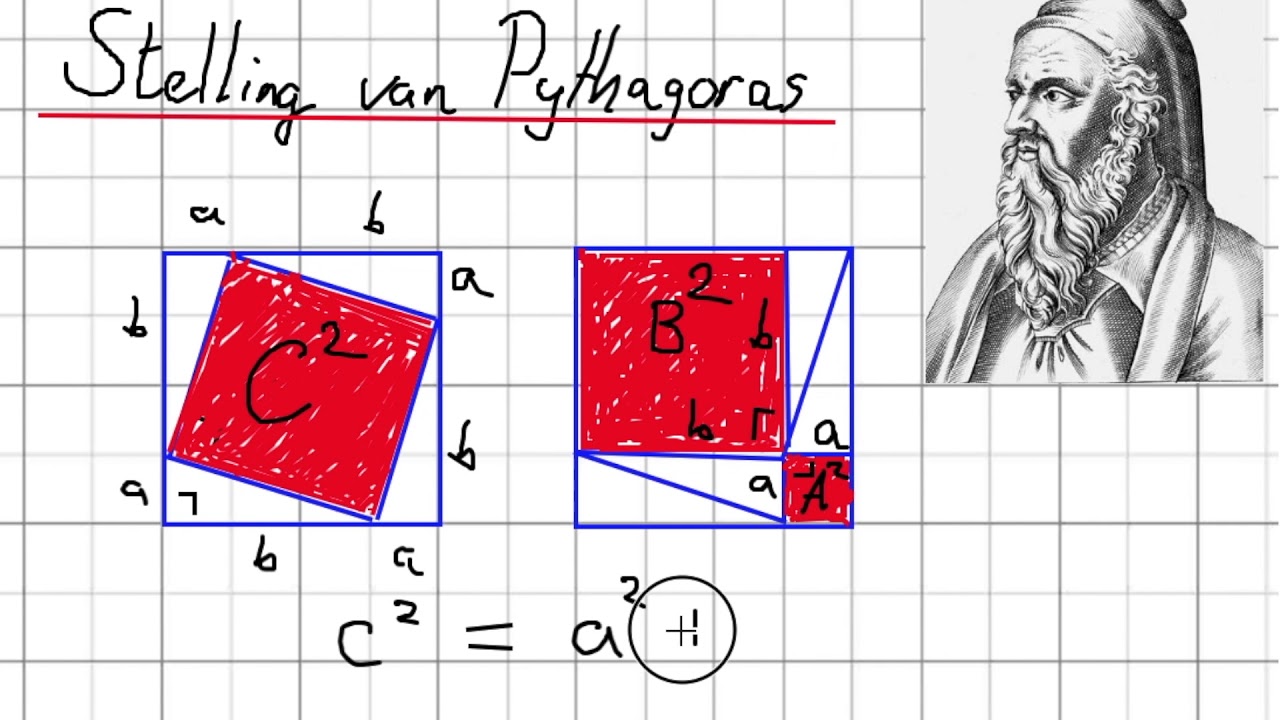
Het is belangrijk om niet alleen de formule te onthouden, maar ook te begrijpen waarom deze waar is. Er zijn vele verschillende bewijzen voor de Stelling van Pythagoras, maar een van de meest aansprekende is een visueel bewijs. Stel je voor dat je een vierkant hebt met zijden van lengte (a + b). Dit vierkant kunnen we op twee verschillende manieren indelen:

We kunnen het vierkant opdelen in vier rechthoekige driehoeken met zijden a, b en c (de hypotenusa), en een kleiner vierkant in het midden met zijden c. De oppervlakte van het grote vierkant is dan gelijk aan 4*(1/2*a*b) + c² = 2ab + c².
We kunnen het vierkant opdelen in een vierkant met zijden a, een vierkant met zijden b en twee rechthoeken met zijden a en b. De oppervlakte van het grote vierkant is dan gelijk aan a² + b² + 2ab.

Omdat we hetzelfde vierkant op twee verschillende manieren hebben ingedeeld, moeten de totale oppervlaktes gelijk zijn:

2ab + c² = a² + b² + 2ab

Als we aan beide kanten 2ab aftrekken, krijgen we:

c² = a² + b²

Dit is precies de Stelling van Pythagoras! Dit visuele bewijs helpt om de stelling te begrijpen in plaats van alleen maar een formule te memoriseren.

Hoe gebruik je de Stelling van Pythagoras?

Laten we eens kijken naar een paar voorbeelden om te zien hoe je de Stelling van Pythagoras in de praktijk kunt gebruiken.

Voorbeeld 1: De ontbrekende zijde vinden

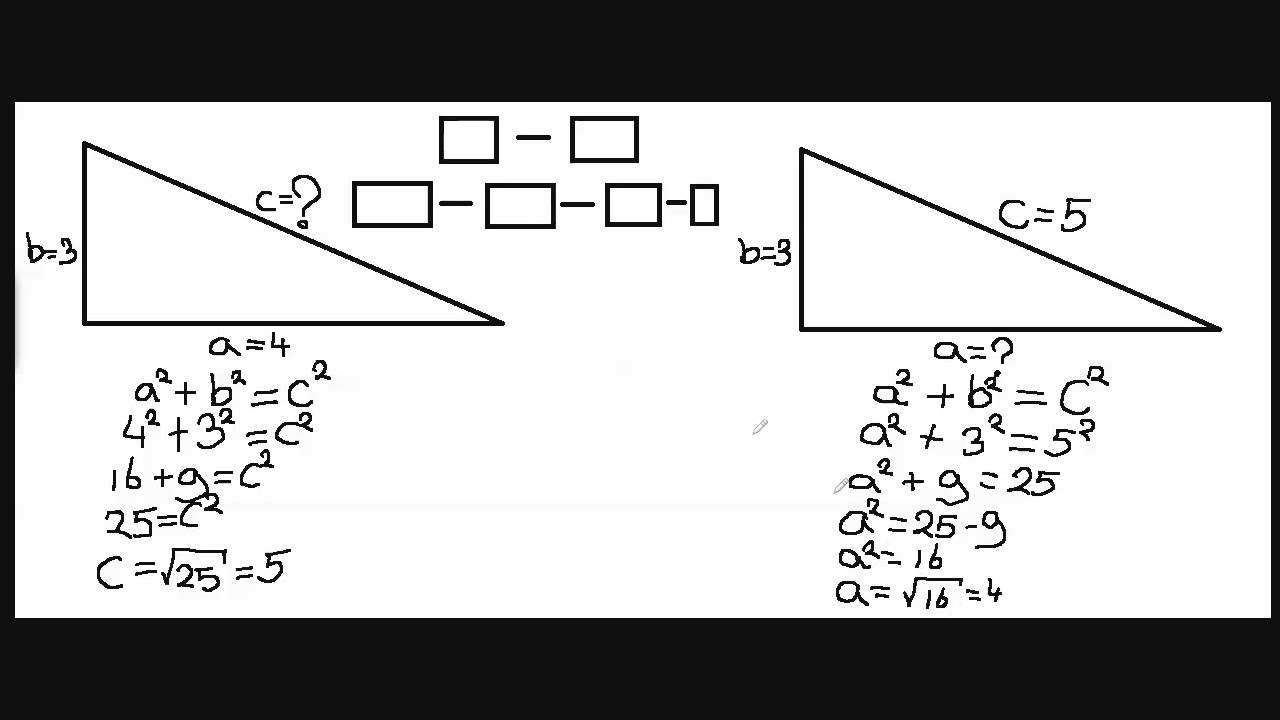
Stel, je hebt een rechthoekige driehoek waarbij de lengte van de ene rechthoekszijde (a) 3 cm is en de lengte van de andere rechthoekszijde (b) 4 cm is. Je wilt de lengte van de hypotenusa (c) vinden.

Volgens de Stelling van Pythagoras:

a² + b² = c²

Substitueer de bekende waarden:

3² + 4² = c²

9 + 16 = c²

25 = c²

Neem de vierkantswortel van beide zijden:

c = √25

c = 5 cm

Dus, de lengte van de hypotenusa is 5 cm.

Voorbeeld 2: Is het een rechthoekige driehoek?

Stel, je hebt een driehoek met zijden van 5 cm, 12 cm en 13 cm. Is dit een rechthoekige driehoek?

Om dit te controleren, passen we de Stelling van Pythagoras toe. De langste zijde (13 cm) is de potentiële hypotenusa. Laten we kijken of de som van de kwadraten van de twee kortere zijden gelijk is aan het kwadraat van de langste zijde:

5² + 12² = 25 + 144 = 169

13² = 169

Omdat 5² + 12² = 13², voldoet deze driehoek aan de Stelling van Pythagoras en is het dus een rechthoekige driehoek.

Voorbeeld 3: Praktische toepassing - Een ladder tegen een muur

Een ladder van 6 meter staat tegen een muur. De voet van de ladder staat 2 meter van de muur. Hoe hoog reikt de ladder op de muur?

In dit geval vormt de muur, de grond en de ladder een rechthoekige driehoek. De ladder is de hypotenusa (c = 6 meter), de afstand van de voet van de ladder tot de muur is de ene rechthoekszijde (a = 2 meter), en de hoogte van de muur tot waar de ladder reikt is de andere rechthoekszijde (b, die we willen vinden).

a² + b² = c²

2² + b² = 6²

4 + b² = 36

b² = 36 - 4

b² = 32

b = √32 ≈ 5.66 meter

Dus de ladder reikt ongeveer 5.66 meter hoog op de muur.

Toepassingen in het dagelijks leven

De Stelling van Pythagoras is meer dan alleen een wiskundige formule; het is een krachtig hulpmiddel met tal van toepassingen in het dagelijks leven:

Architectuur en Bouw: Architecten en bouwvakkers gebruiken de stelling om ervoor te zorgen dat gebouwen hoeken van 90 graden hebben en om afstanden en hoogtes te berekenen. Denk aan het bepalen van de juiste lengte van een dakspar, of het uitzetten van de fundering van een huis.
Navigatie: Navigators gebruiken de stelling om afstanden over land of zee te berekenen, vooral wanneer er geen directe rechte lijn tussen twee punten is.
Timmerwerk: Timmerlieden gebruiken de stelling om perfect rechthoekige hoeken te maken bij het bouwen van kasten, tafels en andere meubels. Een eenvoudige 3-4-5 regel (zijden van 3, 4 en 5 eenheden vormen een rechte hoek) is hierbij een praktische toepassing.
Landmeten: Landmeters gebruiken de stelling om afstanden en hoogtes te meten en om de grenzen van percelen te bepalen.
Computergraphics en Game Development: In computergraphics en game development wordt de stelling gebruikt om afstanden tussen objecten te berekenen, wat essentieel is voor realistische beweging en interactie.

Tips voor het leren en toepassen

Hier zijn enkele tips om de Stelling van Pythagoras beter te begrijpen en toe te passen:

Begrijp het concept: Probeer te begrijpen waarom de stelling waar is, in plaats van alleen de formule te onthouden. De visuele bewijzen kunnen hierbij helpen.
Oefen met voorbeelden: Werk door verschillende voorbeelden om vertrouwd te raken met de stelling en de verschillende manieren waarop je deze kunt toepassen.
Visualiseer het probleem: Teken een diagram van het probleem om te helpen de rechthoekige driehoek te identificeren en de relevante zijden te labelen.
Controleer je antwoord: Controleer of je antwoord logisch is. De hypotenusa moet altijd de langste zijde van de rechthoekige driehoek zijn.
Gebruik online tools: Er zijn veel online calculators die je kunt gebruiken om de Stelling van Pythagoras toe te passen en je antwoorden te controleren.

De Stelling van Pythagoras: Meer dan alleen een formule

De Stelling van Pythagoras is veel meer dan een abstract wiskundig concept. Het is een krachtig instrument dat ons helpt de wereld om ons heen te begrijpen en te navigeren. Door de stelling te begrijpen en toe te passen, krijgen we een dieper inzicht in de principes die ten grondslag liggen aan veel aspecten van ons dagelijks leven.

We hopen dat dit artikel je heeft geholpen om de Stelling van Pythagoras beter te begrijpen. Blijf oefenen en experimenteren, en je zult versteld staan van de mogelijkheden die deze eenvoudige, maar elegante stelling biedt. Wiskunde is niet eng; het is een hulpmiddel om de wereld te begrijpen. Gebruik het!

Dus, de volgende keer dat je een timmerman een perfecte hoek ziet maken, of een architect een indrukwekkend gebouw ziet ontwerpen, denk dan aan de Stelling van Pythagoras en de fundamentele rol die het speelt in onze moderne wereld. Je hebt nu de kennis om de basis te begrijpen!