Hoe Werkt Stelling Van Pythagoras

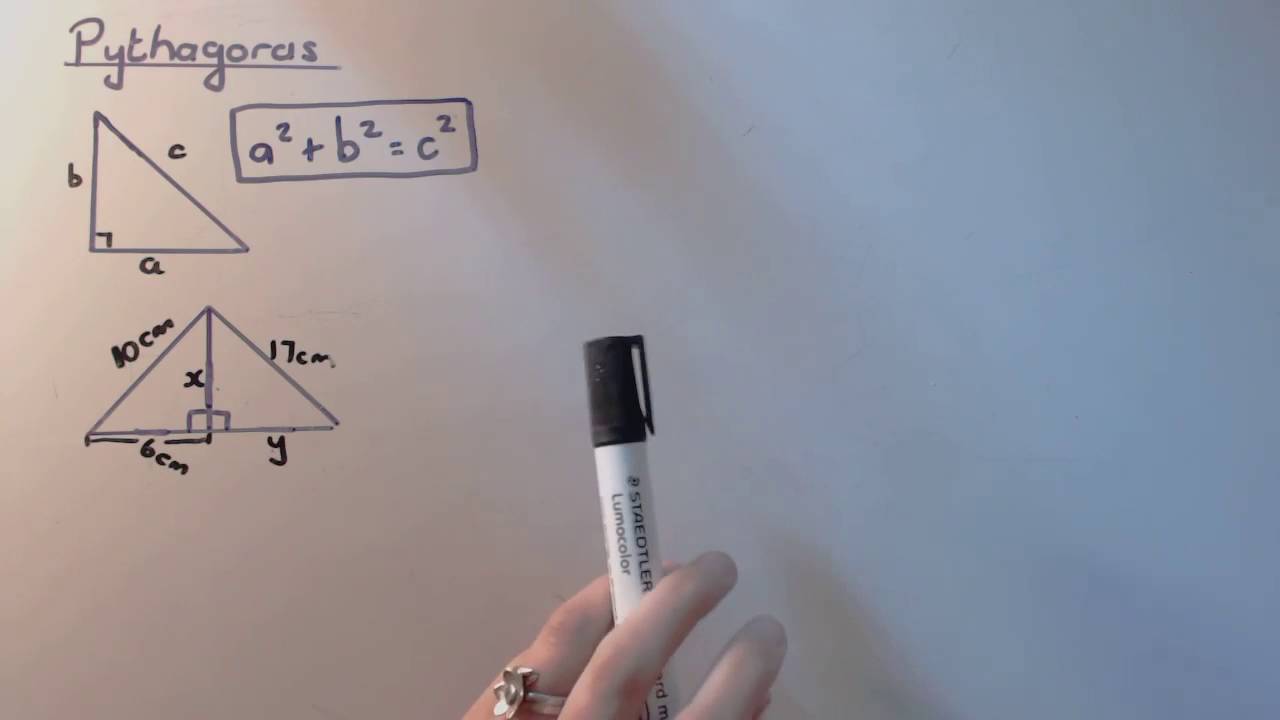
Laten we eerlijk zijn, wiskunde kan soms voelen als een doolhof. Formules zweven rond, concepten lijken abstract, en je vraagt je af wanneer je dit in het echte leven ooit zult gebruiken. De Stelling van Pythagoras is zo'n formule die voor sommigen tot die categorie behoort. Maar geloof me, deze ogenschijnlijk eenvoudige vergelijking, a² + b² = c², is verre van nutteloos. Sterker nog, ze duikt op verrassende plekken op in ons dagelijks leven. We duiken erin, in begrijpelijke taal, zonder de ingewikkelde wiskundejargon.

Wat is de Stelling van Pythagoras eigenlijk?

De Stelling van Pythagoras beschrijft de relatie tussen de zijden van een rechthoekige driehoek. Een rechthoekige driehoek is een driehoek met één hoek van 90 graden, een zogenaamde rechte hoek. De zijde tegenover de rechte hoek noemen we de hypotenusa (meestal aangeduid met 'c'). De andere twee zijden, die de rechte hoek vormen, noemen we de rechthoekszijden (meestal aangeduid met 'a' en 'b').

De stelling zegt dus: de som van de kwadraten van de rechthoekszijden is gelijk aan het kwadraat van de hypotenusa. Simpel gezegd: a² + b² = c².

Een voorbeeld ter illustratie:

Stel je voor dat je een rechthoekige driehoek hebt waarbij de ene rechthoekszijde (a) 3 cm lang is en de andere rechthoekszijde (b) 4 cm lang. Hoe lang is de hypotenusa (c)?

a² = 3² = 9
b² = 4² = 16
a² + b² = 9 + 16 = 25
c² = 25
c = √25 = 5

De hypotenusa is dus 5 cm lang.

Waarom is dit belangrijk? De impact in de echte wereld

Je vraagt je wellicht af: "Leuk die wiskunde, maar waar gebruik ik dit nou eigenlijk voor?". Nou, verrassend veel!

Bouwkunde en Architectuur: Architecten en bouwkundigen gebruiken de Stelling van Pythagoras constant bij het ontwerpen en bouwen van gebouwen, bruggen en andere constructies. Denk aan het berekenen van de lengte van een dakspant, het uitzetten van hoeken of het zorgen voor rechte muren.
Navigatie: Navigators gebruiken de stelling om afstanden te berekenen en routes uit te stippelen, vooral in combinatie met geografische coördinaten.
Timmerwerk en Klussen: Bij het plaatsen van planken, het bouwen van een schutting of het installeren van een trap komt de Stelling van Pythagoras goed van pas om ervoor te zorgen dat alles haaks en recht is.
Games en Computergraphics: Game-ontwikkelaars gebruiken de stelling om afstanden tussen objecten te berekenen, botsingen te detecteren en realistische bewegingen te simuleren.
Landmeetkunde: Landmeters gebruiken de stelling om afstanden en hoogtes te bepalen bij het in kaart brengen van terreinen.

Kortom, de Stelling van Pythagoras is een fundamenteel principe dat in talloze technische en praktische toepassingen wordt gebruikt. Zonder deze stelling zouden veel van de structuren en technologieën die we als vanzelfsprekend beschouwen, niet bestaan.

Counterpoints: Is het écht zo onmisbaar?

Hoewel de Stelling van Pythagoras ongelooflijk nuttig is, zijn er ook situaties waarin andere wiskundige concepten relevanter zijn. In complexe geometrische berekeningen of in de hogere wiskunde zijn er vaak geavanceerdere methoden die efficiënter zijn. Ook is de stelling direct alleen toepasbaar op rechthoekige driehoeken. Echter, zelfs in die gevallen dient de Stelling van Pythagoras vaak als een basisprincipe waarop complexere berekeningen voortbouwen. Het is als het ware een bouwsteen voor andere wiskundige concepten.

Daarnaast is het waar dat moderne technologie, zoals GPS en computerprogramma's, veel van de berekeningen die vroeger handmatig werden uitgevoerd met de Stelling van Pythagoras, nu automatisch kan uitvoeren. Toch is het begrijpen van het principe achter deze berekeningen cruciaal voor het interpreteren van de resultaten en het oplossen van problemen. Het is het verschil tussen een knop indrukken en daadwerkelijk begrijpen wat er gebeurt.

Hoe je de Stelling van Pythagoras kunt begrijpen en toepassen

Het begrijpen van de Stelling van Pythagoras hoeft niet ingewikkeld te zijn. Hier zijn een paar tips:

Visualiseer het: Teken zelf rechthoekige driehoeken en meet de zijden. Bereken vervolgens de lengte van de hypotenusa met de stelling en controleer of je berekening klopt.
Gebruik concrete voorbeelden: Zoek voorbeelden in je omgeving waar je de Stelling van Pythagoras kunt toepassen. Denk aan het berekenen van de diagonaal van een rechthoekig scherm of het bepalen van de lengte van een kabel die een rechthoekig terrein overspant.
Oefen: Oefening baart kunst. Maak verschillende opgaven en probeer de stelling in verschillende contexten toe te passen. Er zijn online veel oefeningen en tutorials te vinden.
Begrijp het concept, niet alleen de formule: Het is belangrijk om te begrijpen waarom de stelling werkt, niet alleen hoe je de formule moet invullen. Zoek naar uitleg en bewijzen van de stelling om een dieper begrip te krijgen.
Gebruik online tools: Er zijn verschillende online tools en rekenmachines beschikbaar die je kunnen helpen bij het berekenen van de lengte van de zijden van een rechthoekige driehoek. Deze tools kunnen handig zijn om je antwoorden te controleren en je begrip te vergroten.

Oefenopgave:

Je wilt een ladder tegen een muur plaatsen. De ladder is 6 meter lang en de voet van de ladder staat 2 meter van de muur af. Hoe hoog reikt de ladder tegen de muur?

Probeer deze opgave zelf op te lossen met de Stelling van Pythagoras. Je kunt de oplossing online vinden om je antwoord te controleren.

Oplossingsgericht denken: van theorie naar praktijk

In plaats van alleen maar de problemen te benoemen die wiskunde soms met zich meebrengt, is het belangrijk om te focussen op oplossingen. De Stelling van Pythagoras is een perfect voorbeeld van een oplossing voor een specifiek geometrisch probleem. Door het probleem te begrijpen, de juiste formule toe te passen en de berekeningen correct uit te voeren, kunnen we concrete antwoorden en oplossingen vinden.

Het gaat erom de Stelling van Pythagoras te zien als een tool die je kunt gebruiken om problemen op te lossen, in plaats van als een obstakel. Door te oefenen en de stelling in verschillende contexten toe te passen, zul je merken dat je steeds beter in staat bent om complexe problemen op te lossen en de wereld om je heen beter te begrijpen.

Denk bijvoorbeeld aan het bouwen van een pergola in je tuin. Door de Stelling van Pythagoras te gebruiken, kun je ervoor zorgen dat de palen perfect haaks staan en dat de constructie stevig en stabiel is. Of denk aan het plannen van een wandeltocht. Met behulp van kaarten en de Stelling van Pythagoras kun je de afstanden tussen verschillende punten berekenen en een realistische route uitstippelen.

De mogelijkheden zijn eindeloos. Het enige wat je nodig hebt is een beetje creativiteit en de bereidheid om de Stelling van Pythagoras in de praktijk te brengen.

Tot slot: Een uitnodiging tot reflectie

De Stelling van Pythagoras is meer dan alleen een wiskundige formule; het is een krachtig hulpmiddel dat ons kan helpen de wereld om ons heen beter te begrijpen en problemen op te lossen. Nu je een beter begrip hebt van deze stelling, waar zie jij mogelijkheden om deze in je eigen leven toe te passen?

Misschien bij je volgende doe-het-zelf project, bij het plannen van een reis, of gewoon om je ruimtelijk inzicht te verbeteren. De sleutel is om open te staan voor de mogelijkheden en de stelling niet te zien als een abstract concept, maar als een praktische tool die je kan helpen je doelen te bereiken.

Welke uitdaging ga jij aan met de Stelling van Pythagoras in je achterhoofd?