Hoek Berekenen Driehoek 90 Graden

Heb je je ooit afgevraagd hoe je de hoeken in een rechthoekige driehoek kunt berekenen? Of je nu een student bent die worstelt met meetkunde, een doe-het-zelver die een perfect schuine hoek nodig heeft, of gewoon iemand met een gezonde interesse in wiskunde, dit artikel is voor jou. We gaan je stap voor stap begeleiden door de methoden en principes die je nodig hebt om dit te doen.

Wat is een rechthoekige driehoek?

Laten we beginnen met de basis. Een rechthoekige driehoek is een driehoek waarin één van de hoeken precies 90 graden is. Deze hoek wordt vaak aangeduid met een klein vierkantje in de hoek. De zijde tegenover de rechte hoek wordt de hypotenusa genoemd, en de andere twee zijden worden de rechthoekszijden of cathetussen genoemd.

Waarom is dit belangrijk? Omdat de rechte hoek ons een heleboel voordelen geeft bij het berekenen van de andere hoeken en zijden. Denk aan de stelling van Pythagoras en de goniometrische functies – allemaal gebaseerd op de speciale eigenschappen van rechthoekige driehoeken.

De som van de hoeken in een driehoek

Een fundamenteel principe dat je moet kennen is dat de som van de hoeken in elke driehoek altijd 180 graden is. Dit geldt dus ook voor rechthoekige driehoeken. Aangezien we al weten dat één hoek 90 graden is, betekent dit dat de som van de andere twee hoeken ook 90 graden moet zijn. Dit maakt het berekenen van de overige hoeken een stuk eenvoudiger.

Stel je voor: Je hebt een rechthoekige driehoek met een hoek van 30 graden. Dan is de derde hoek automatisch 180 - 90 - 30 = 60 graden.

Methoden om hoeken te berekenen

Er zijn verschillende manieren om de hoeken in een rechthoekige driehoek te berekenen, afhankelijk van de informatie die je al hebt. We zullen de meest gangbare methoden bespreken:

1. Gebruik van de stelling van Pythagoras

De stelling van Pythagoras is een krachtig hulpmiddel dat de relatie tussen de zijden van een rechthoekige driehoek beschrijft. De stelling zegt: a² + b² = c², waarbij:

a en b de lengtes van de rechthoekszijden zijn
c de lengte van de hypotenusa is

Hoewel de stelling van Pythagoras direct geen hoeken berekent, kan je, zodra je de lengtes van alle drie de zijden hebt, de goniometrische functies gebruiken om de hoeken te bepalen. We komen hier later op terug.

Voorbeeld: Stel dat de rechthoekszijden van een rechthoekige driehoek 3 cm en 4 cm zijn. Dan is de hypotenusa √(3² + 4²) = √(9 + 16) = √25 = 5 cm.

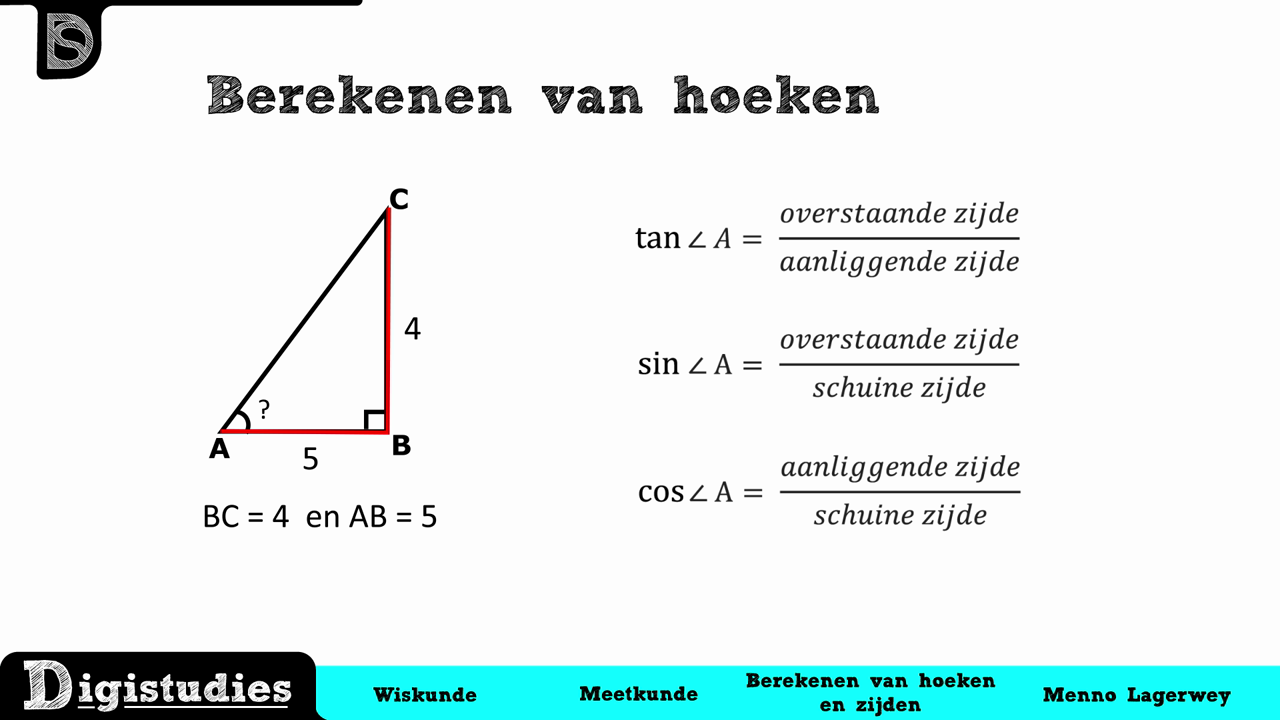
2. Gebruik van goniometrische functies

Goniometrische functies, zoals sinus (sin), cosinus (cos) en tangens (tan), leggen een verband tussen de hoeken en de verhoudingen van de zijden van een rechthoekige driehoek.

Sinus (sin) = Overstaande zijde / Hypotenusa
Cosinus (cos) = Aanliggende zijde / Hypotenusa
Tangens (tan) = Overstaande zijde / Aanliggende zijde

Hoe gebruik je dit? Stel dat je de lengte van de overstaande zijde en de hypotenusa kent. Dan kun je de sinus van de hoek berekenen door de overstaande zijde te delen door de hypotenusa. Om de hoek zelf te vinden, gebruik je de inverse sinus functie (sin^-1 of arcsin) op je rekenmachine.

Hetzelfde geldt voor cosinus en tangens. Als je bijvoorbeeld de lengte van de aanliggende zijde en de hypotenusa kent, gebruik je de cosinus en de inverse cosinus (cos^-1 of arccos) om de hoek te vinden. Als je de lengte van de overstaande en aanliggende zijde kent, gebruik je de tangens en de inverse tangens (tan^-1 of arctan).

Voorbeeld: Stel dat de overstaande zijde 4 cm is en de hypotenusa 5 cm. Dan is sin(hoek) = 4/5 = 0.8. De hoek is dan sin^-1(0.8) ≈ 53.13 graden.

3. Gebruik van de som van de hoeken

Zoals eerder vermeld, is de som van de hoeken in een driehoek altijd 180 graden. In een rechthoekige driehoek is één hoek 90 graden. Als je één van de andere hoeken kent, kun je de derde hoek eenvoudig berekenen door:

Hoek 3 = 180 - 90 - Hoek 2

Voorbeeld: Je weet dat een van de hoeken in een rechthoekige driehoek 25 graden is. Dan is de derde hoek 180 - 90 - 25 = 65 graden.

Wanneer welke methode gebruiken?

De keuze van de methode hangt af van welke informatie je tot je beschikking hebt:

Als je de lengtes van alle drie de zijden kent: Gebruik de stelling van Pythagoras om te bevestigen dat het een rechthoekige driehoek is, en gebruik vervolgens goniometrische functies (sin, cos, tan) om de hoeken te berekenen.
Als je de lengte van twee zijden kent en weet dat het een rechthoekige driehoek is: Gebruik goniometrische functies (sin, cos, tan) om de hoeken te berekenen.
Als je één van de hoeken (anders dan de rechte hoek) kent: Gebruik de eigenschap dat de som van de hoeken in een driehoek 180 graden is om de andere hoek te berekenen.

Praktische toepassingen

Het berekenen van hoeken in rechthoekige driehoeken is niet alleen een abstracte wiskundige oefening. Het heeft veel praktische toepassingen in het dagelijks leven en in verschillende vakgebieden:

Bouwkunde: Om ervoor te zorgen dat gebouwen en constructies stabiel en veilig zijn, is het cruciaal om de juiste hoeken te gebruiken.
Navigatie: Voor het bepalen van de positie en richting, bijvoorbeeld bij het varen of vliegen.
Engineering: Bij het ontwerpen van machines, bruggen en andere structuren.
Grafisch ontwerp: Voor het creëren van perspectief en het tekenen van objecten in de juiste verhoudingen.
Timmerwerk: Voor het zagen van hout onder de juiste hoek bij het maken van meubels of andere constructies.

Veelgemaakte fouten en hoe ze te vermijden

Bij het berekenen van hoeken in rechthoekige driehoeken kunnen er fouten optreden. Hier zijn enkele veelvoorkomende fouten en tips om ze te vermijden:

Verkeerde zijden gebruiken in de goniometrische functies: Zorg ervoor dat je de juiste zijden (overstaand, aanliggend, hypotenusa) identificeert voordat je de sinus, cosinus of tangens berekent.
De inverse functie vergeten: Vergeet niet de inverse functie (sin^-1, cos^-1, tan^-1) te gebruiken om de hoek zelf te vinden, nadat je de sinus, cosinus of tangens hebt berekend.
Rekenmachine in de verkeerde modus: Controleer of je rekenmachine in de juiste modus staat (graden of radialen). Voor de meeste praktische toepassingen wil je graden gebruiken.
Afgeronde getallen te vroeg gebruiken: Rond getallen zo laat mogelijk af om afrondingsfouten te minimaliseren.

Oefenen baart kunst

Zoals met alles, is oefening de sleutel tot het beheersen van het berekenen van hoeken in rechthoekige driehoeken. Probeer verschillende voorbeelden en oefen met verschillende methoden. Gebruik online tools of wiskundeboeken om meer oefeningen te vinden.

Hier zijn enkele oefenopgaven:

Een rechthoekige driehoek heeft een hypotenusa van 10 cm en een rechthoekszijde van 6 cm. Bereken de andere rechthoekszijde en de twee scherpe hoeken.
In een rechthoekige driehoek is een hoek 40 graden. Bereken de andere scherpe hoek.
Een rechthoekige driehoek heeft een overstaande zijde van 5 cm en een aanliggende zijde van 12 cm. Bereken de hypotenusa en de twee scherpe hoeken.

Conclusie

Het berekenen van hoeken in rechthoekige driehoeken is een waardevolle vaardigheid met toepassingen in diverse gebieden. Door de principes van de stelling van Pythagoras, goniometrische functies en de som van de hoeken te begrijpen, kun je deze berekeningen met vertrouwen uitvoeren. Onthoud: oefening baart kunst, dus blijf oefenen en experimenteren! We hopen dat dit artikel je de tools en het inzicht heeft gegeven om je wiskundige vaardigheden verder te ontwikkelen en met succes hoeken in rechthoekige driehoeken te berekenen. Veel succes!