Hoeveel Gebogen Zijvlakken Heeft Een Cilinder

Heb je je ooit afgevraagd hoeveel gebogen zijvlakken een cilinder eigenlijk heeft? Het lijkt misschien een eenvoudige vraag, maar het antwoord kan verrassender zijn dan je denkt. In dit artikel duiken we dieper in de geometrie van de cilinder en proberen we helderheid te scheppen. Misschien denk je: "Waarom zou ik me hier druk om maken?" Nou, kennis van basisvormen zoals de cilinder is essentieel in talloze vakgebieden, van architectuur en engineering tot design en zelfs in je dagelijks leven bij het herkennen en begrijpen van objecten om je heen.

Wat is een Cilinder?

Laten we beginnen met de basis. Een cilinder is een driedimensionale geometrische vorm met twee identieke, evenwijdige cirkelvormige bases die verbonden zijn door een gebogen oppervlak. Je kunt je het voorstellen als een blikje soep, een rol keukenpapier, of een pijp. Belangrijk om te onthouden is dat we hier spreken over een rechte cilinder, waarbij de as loodrecht staat op de basisvlakken.

De Onderdelen van een Cilinder

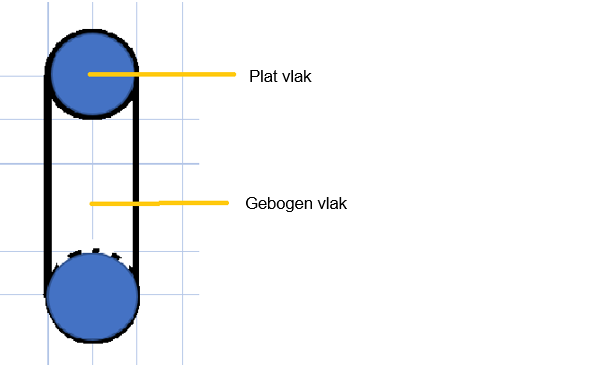
• Basisvlakken: Twee cirkelvormige vlakken aan de uiteinden.
• Gebogen Zijvlak: Het oppervlak dat de twee basisvlakken verbindt.
• Hoogte: De afstand tussen de twee basisvlakken.

Hoeveel Gebogen Zijvlakken?

Dit is waar het interessant wordt. De vraag is niet zo eenvoudig als het lijkt, omdat het antwoord afhangt van hoe je het woord "zijvlak" interpreteert. Sommigen zouden beargumenteren dat een cilinder maar één gebogen zijvlak heeft, namelijk het oppervlak dat de twee cirkels verbindt. Dit is het meest gangbare en logische antwoord. Stel je voor dat je een stuk papier rondom een cilindervormig object wikkelt. Het papier vormt één continu oppervlak, zonder duidelijke scheidingen of afzonderlijke vlakken.

Anderen daarentegen, kunnen stellen dat een cilinder oneindig veel gebogen zijvlakken heeft. Dit argument komt voort uit het idee dat een gebogen oppervlak kan worden benaderd door een oneindig aantal oneindig kleine platte vlakken. Denk aan een digitale weergave van een cilinder op een computerscherm. Als je voldoende inzoomt, zie je dat de curve is opgebouwd uit kleine pixels, die in feite kleine vierkantjes zijn. Op dezelfde manier zou je het gebogen oppervlak van een cilinder kunnen opdelen in oneindig veel infinitesimale gebogen "vlakjes".

Hoewel beide perspectieven hun eigen logica hebben, is het in de meeste contexten correct om te zeggen dat een cilinder één gebogen zijvlak heeft.

Waarom is dit Belangrijk?

Misschien denk je nu: "Leuk en aardig, maar wat heb ik hier aan?". Nou, het begrijpen van de eigenschappen van basisvormen zoals de cilinder is cruciaal in veel gebieden:

• Architectuur en Engineering: Cilindrische vormen worden veel gebruikt in constructies, zoals pijlers, buizen en tanks. Het berekenen van de oppervlakte en het volume van cilinders is essentieel voor het ontwerpen van structuren die sterk en veilig zijn.
• Productie: Cilinders komen voor in talloze producten, van blikjes frisdrank tot zuigers in motoren. Het begrijpen van de geometrie van cilinders is belangrijk voor het efficiënt ontwerpen en fabriceren van deze producten.
• Wiskunde en Natuurkunde: De cilinder dient als een belangrijk voorbeeld in de studie van geometrie en calculus. Het berekenen van oppervlaktes, volumes en integratie over cilindrische coördinaten zijn fundamentele concepten.
• Dagelijks Leven: Denk aan het berekenen hoeveel verf je nodig hebt voor een cilindervormige plantenbak, of het inschatten van de hoeveelheid vloeistof in een cilindervormige container.

Contra-argumenten en Misvattingen

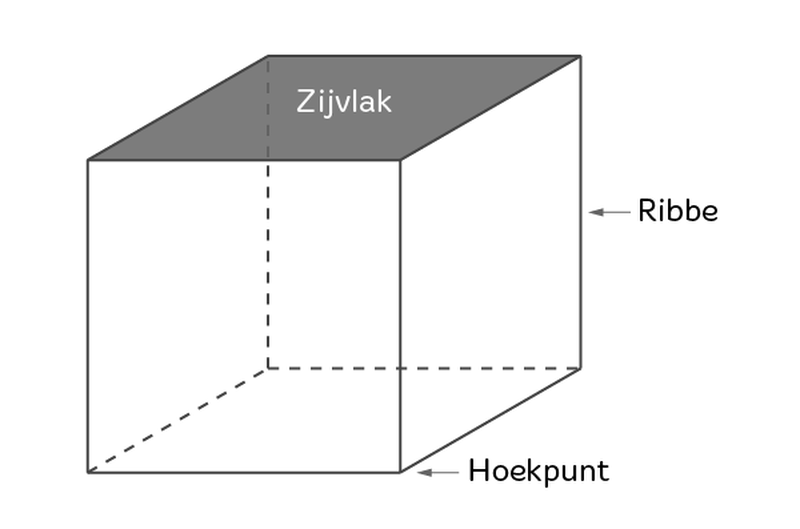
Een veel voorkomende misvatting is dat een cilinder een prisma is met oneindig veel zijden. Hoewel dit een nuttige analogie kan zijn om de vorm te begrijpen, is het belangrijk om te onthouden dat een prisma *platte* zijvlakken heeft, terwijl een cilinder een *gebogen* zijvlak heeft. Het is deze kromming die het onderscheidend maakt.

Sommigen verwarren ook de *mantel* van een cilinder met de zijvlakken. De mantel is het gebogen oppervlak, terwijl "zijvlakken" in deze context verwijzen naar individuele platte of gebogen oppervlakken die de vorm vormen. De mantel *is* dus het gebogen zijvlak.

Oplossingen en Toepassingen

Laten we eens kijken naar enkele praktische toepassingen van deze kennis:

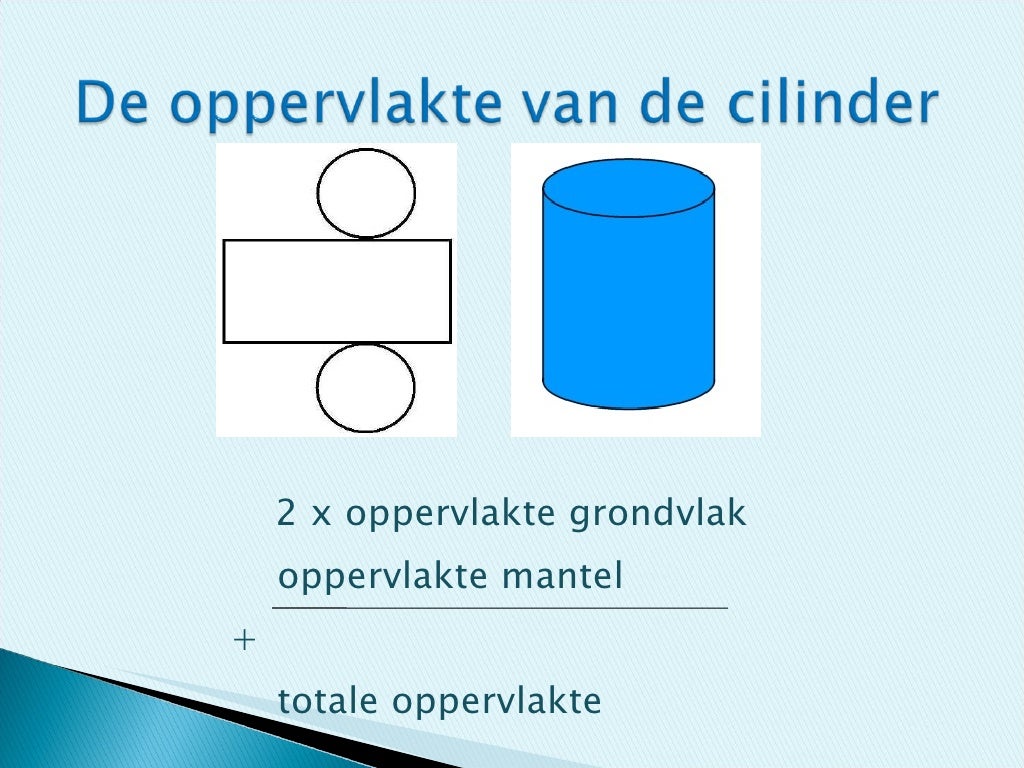
• Oppervlakteberekening: De totale oppervlakte van een cilinder is 2πr² + 2πrh, waarbij r de straal van de basis is en h de hoogte. Dit is cruciaal voor het berekenen van de hoeveelheid materiaal die nodig is om een cilinder te maken.
• Volumeberekening: Het volume van een cilinder is πr²h. Dit is belangrijk voor het bepalen van de capaciteit van een cilindervormige container.
• Optimalisatie: In de engineering kan het optimaliseren van de vorm van een cilinder leiden tot efficiëntere ontwerpen, bijvoorbeeld bij het minimaliseren van het materiaalgebruik of het maximaliseren van de sterkte.

Er zijn online rekenmachines en tools beschikbaar die je kunnen helpen bij het berekenen van de oppervlakte en het volume van cilinders. Deze tools zijn handig voor zowel studenten als professionals die snel en nauwkeurig berekeningen moeten uitvoeren.

Conclusie

Samenvattend: een cilinder heeft, in de meest gangbare interpretatie, één gebogen zijvlak en twee cirkelvormige basisvlakken. Hoewel er argumenten zijn voor het idee van oneindig veel infinitesimale vlakken, is het enkelvoudige gebogen vlak de meest praktische en algemeen aanvaarde definitie. Het begrijpen van deze fundamentele geometrische eigenschappen is essentieel in een breed scala aan vakgebieden en kan je helpen bij het oplossen van problemen in zowel professionele als alledaagse situaties. Het is een eenvoudig concept met verreikende implicaties.

Dus, de volgende keer dat je een blikje soep ziet, denk dan even na over de geometrie van de cilinder en de manieren waarop deze vorm onze wereld beïnvloedt. Welke andere alledaagse objecten hebben jou aan het denken gezet over geometrie?