Hoeveel Graden Is Een Driehoek

De hoeken van een driehoek vormen een fundamenteel concept in de meetkunde. Vrijwel iedereen heeft er op de basisschool wel eens van gehoord, maar de exacte details en implicaties kunnen soms vervagen. Dit artikel duikt diep in de eigenschappen van driehoeken, specifiek met betrekking tot de graden van hun hoeken, en biedt een heldere uitleg, ondersteund door voorbeelden uit de praktijk.

De Basis: De Som van de Hoeken

Het kernpunt van het verhaal is dat de som van de binnenhoeken van elke driehoek, ongeacht de vorm of grootte, altijd 180 graden is. Dit is een universele regel in de Euclidische meetkunde. Het maakt niet uit of je een scherphoekige, stomphoekige, rechthoekige, gelijkzijdige of gelijkbenige driehoek hebt, de som van de hoeken is onveranderlijk 180 graden.

Deze regel is niet zomaar een feitje om te onthouden; het is een cruciale bouwsteen voor veel geometrische berekeningen en bewijzen.

Waarom 180 Graden?

Je kunt de basis leggen voor het begrip van deze 180-graden regel door een eenvoudige activiteit te demonstreren. Teken een willekeurige driehoek op een stuk papier. Knip de drie hoeken uit. Leg deze drie hoeken vervolgens tegen elkaar aan, zodanig dat de hoekpunten samenkomen. Je zult zien dat de hoeken samen precies een rechte lijn vormen, en een rechte lijn is gedefinieerd als een hoek van 180 graden.

Een formeler bewijs betrekt het concept van evenwijdige lijnen en verwisselende binnenhoeken. Stel je een lijn voor die evenwijdig is aan een van de zijden van de driehoek, en die door het tegenoverliggende hoekpunt gaat. Door de eigenschappen van evenwijdige lijnen kun je aantonen dat de hoeken die gevormd worden door de andere twee zijden met deze evenwijdige lijn gelijk zijn aan de overeenkomstige hoeken van de driehoek. Deze hoeken samen vormen een gestrekte hoek (180 graden), wat bewijst dat de som van de hoeken van de driehoek ook 180 graden is.

Verschillende soorten Driehoeken en hun Hoeken

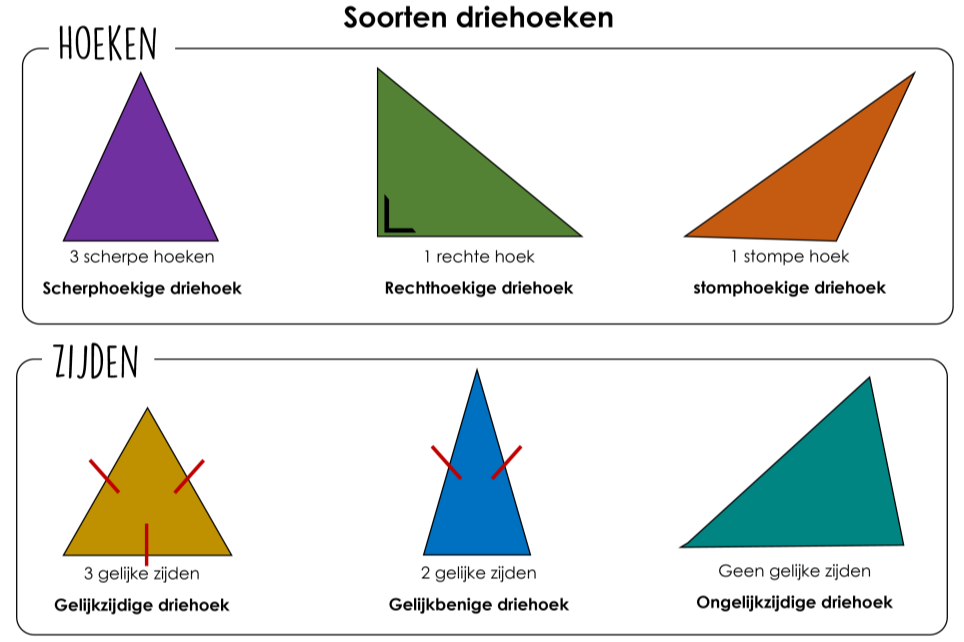
Hoewel de som van de hoeken altijd 180 graden is, variëren de individuele hoeken afhankelijk van het type driehoek.

Rechthoekige Driehoeken

Een rechthoekige driehoek heeft één hoek die exact 90 graden is (een rechte hoek). De andere twee hoeken zijn altijd scherp (minder dan 90 graden) en de som van deze twee scherpe hoeken is 90 graden. Dit komt omdat 180 (totale hoeken) - 90 (rechte hoek) = 90 graden.

Scherphoekige Driehoeken

Een scherphoekige driehoek heeft drie hoeken die elk minder dan 90 graden zijn. Alle hoeken zijn dus 'scherp'.

Stomphoekige Driehoeken

Een stomphoekige driehoek heeft één hoek die meer dan 90 graden is (een stompe hoek). De andere twee hoeken zijn scherp.

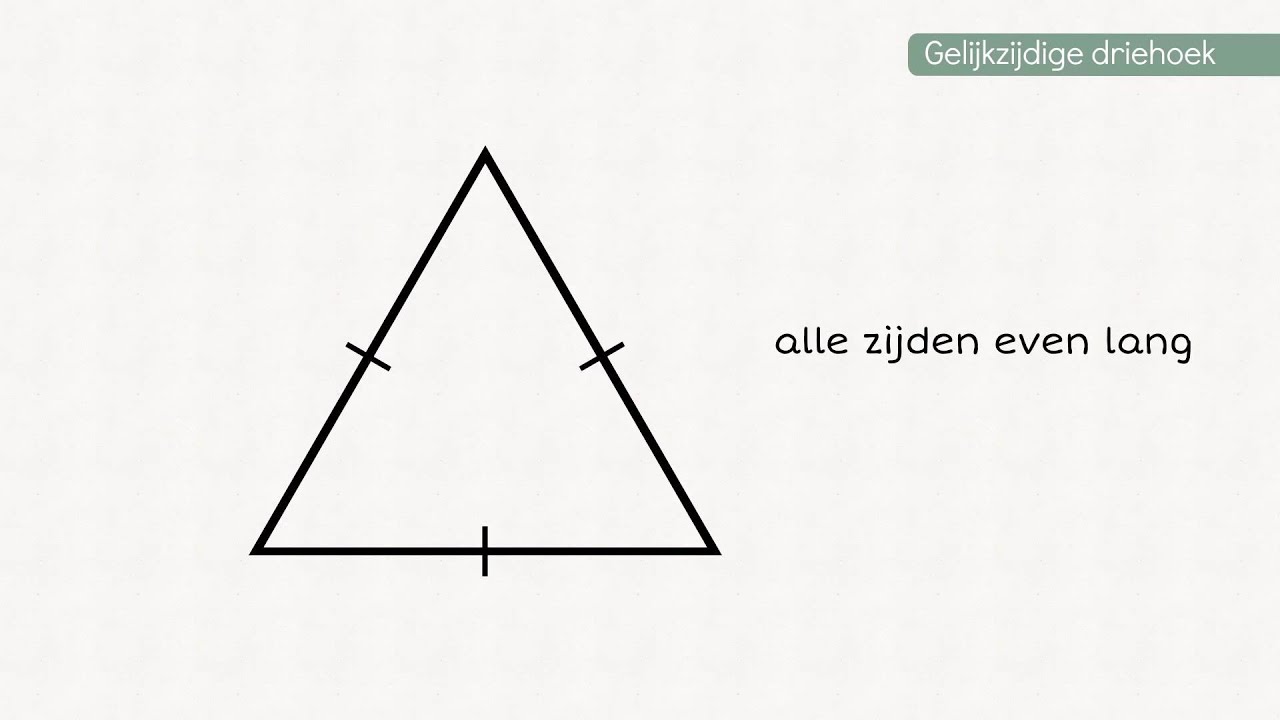
Gelijkzijdige Driehoeken

Een gelijkzijdige driehoek is een speciaal geval. Omdat alle zijden gelijk zijn, zijn ook alle hoeken gelijk. Dit betekent dat elke hoek 180 graden / 3 = 60 graden is. Een gelijkzijdige driehoek is dus altijd scherphoekig.

Gelijkbenige Driehoeken

Een gelijkbenige driehoek heeft twee zijden die gelijk zijn. De hoeken tegenover deze gelijke zijden zijn ook gelijk aan elkaar. Als je de waarde van één van deze gelijke hoeken weet, kun je de derde hoek berekenen door: 180 graden - (2 * de bekende hoek).

Toepassingen in de Praktijk

Het begrip van de hoeken van een driehoek is niet alleen relevant voor wiskunde-examens. Het heeft veel praktische toepassingen in verschillende velden:

• Architectuur en Bouwkunde: Driehoeken zijn cruciaal voor het ontwerpen van stevige structuren. Denk aan de spanten van een dak of de frames van bruggen. De hoeken van de driehoeken bepalen de sterkte en stabiliteit van de constructie. Architecten en bouwkundigen gebruiken trigonometrie (dat gebaseerd is op driehoeken) om hoeken en afstanden nauwkeurig te berekenen.
• Navigatie: Zeelieden en piloten gebruiken driehoeksmeting om hun positie te bepalen. Door de hoeken tussen verschillende herkenningspunten te meten, kunnen ze hun exacte locatie op een kaart bepalen.
• Landmeten: Landmeters gebruiken driehoeken om land te meten en kaarten te maken. Ze gebruiken theodolieten (instrumenten voor het meten van hoeken) om de hoeken van driehoeken te meten en zo afstanden en hoogtes te berekenen.
• Computergraphics en Game Development: Driehoeken zijn de basis van veel 3D-modellen. Computers gebruiken de hoeken en coördinaten van de hoekpunten van de driehoeken om 3D-objecten te renderen en te manipuleren.

Voorbeeld: Stel je voor dat je een schuin dak wilt bouwen. Je weet dat de basis van het dak 8 meter breed is en de hoogte 3 meter. Je kunt trigonometrie (of eenvoudiger, de stelling van Pythagoras en de inverse tangens functie) gebruiken om de hoek van het dak te berekenen, zodat het water correct afvoert en de structurele integriteit behouden blijft.

Data: Onderzoek naar bruggenbouw heeft aangetoond dat bruggen die gebaseerd zijn op driehoeksconstructies (zoals vakwerkbruggen) significant sterker en stabieler zijn dan bruggen die gebaseerd zijn op andere vormen. Dit komt door de inherente stijfheid van de driehoek.

Uitzonderingen?

De regel dat de som van de hoeken van een driehoek 180 graden is, geldt binnen de Euclidische meetkunde, de meest gangbare vorm van meetkunde die we in het dagelijks leven ervaren. Echter, in niet-Euclidische meetkunde, zoals sferische meetkunde (meetkunde op het oppervlak van een bol), is dit niet het geval.

Op het oppervlak van een bol kan de som van de hoeken van een driehoek meer dan 180 graden zijn. Denk bijvoorbeeld aan een driehoek die gevormd wordt door de Noordpool en twee punten op de evenaar, elk 90 graden van elkaar verwijderd in lengte. De hoeken bij de evenaar zijn beide 90 graden, en de hoek op de Noordpool is ook 90 graden, waardoor de som 270 graden is!

Deze afwijkingen van de Euclidische meetkunde zijn belangrijk in contexten zoals navigatie over lange afstanden op de aarde, waar de kromming van de aarde een rol speelt.

Conclusie

De 180-graden regel voor de som van de hoeken van een driehoek is een fundamenteel concept in de meetkunde. Het is niet alleen een abstracte regel, maar heeft ook talloze praktische toepassingen in de architectuur, navigatie, landmeten en computermodellering. Door de verschillende soorten driehoeken en hun eigenschappen te begrijpen, kan men complexe problemen oplossen en stevige constructies ontwerpen.

Dus, de volgende keer dat je een driehoek ziet, of het nu een verkeersbord is, de spant van een dak, of een 3D-model op een computerscherm, onthoud dan dat de som van de hoeken altijd (meestal) 180 graden is. Daag jezelf uit om de hoeken van objecten om je heen te schatten en te begrijpen hoe deze principes worden toegepast in de echte wereld.