Hoeveel Graden Is Een Vierhoek

De vraag "Hoeveel graden is een vierhoek?" lijkt misschien simpel, maar het antwoord vereist een goed begrip van geometrie en de eigenschappen van verschillende vierhoeken. Dit artikel duikt diep in de hoeken van vierhoeken, verkent verschillende soorten en geeft concrete voorbeelden om het concept helder te maken. We zullen zien dat hoewel de som van de hoeken altijd hetzelfde is, de individuele hoeken sterk kunnen variëren.

De Basis: Som van de Hoeken in een Vierhoek

De cruciale eigenschap die alle vierhoeken delen, is dat de som van hun binnenhoeken altijd 360 graden is. Dit geldt ongeacht de vorm van de vierhoek – of het nu een perfect vierkant, een langwerpige rechthoek, een scheve parallellogram of een onregelmatige trapezium is. Dit fundamentele feit is essentieel om veel geometrische problemen op te lossen.

Maar waar komt die 360 graden vandaan? Een eenvoudige manier om dit te begrijpen, is door een vierhoek te verdelen in twee driehoeken. Teken een diagonaal in de vierhoek (een lijn van de ene hoek naar de tegenoverliggende hoek). Elke driehoek heeft een hoekensom van 180 graden. Aangezien de vierhoek nu bestaat uit twee driehoeken, is de totale hoekensom 2 * 180 = 360 graden.

Bewijs via Driehoeken

Laten we dit nog eens benadrukken. Neem een willekeurige vierhoek ABCD. Teken diagonaal AC. Nu heb je twee driehoeken: driehoek ABC en driehoek ADC.

We weten dat:

• Hoek BAC + Hoek ABC + Hoek BCA = 180 graden (driehoek ABC)
• Hoek DAC + Hoek ADC + Hoek DCA = 180 graden (driehoek ADC)

Als we deze twee vergelijkingen bij elkaar optellen, krijgen we:

(Hoek BAC + Hoek ABC + Hoek BCA) + (Hoek DAC + Hoek ADC + Hoek DCA) = 360 graden

Door hoeken te combineren, zien we dat dit hetzelfde is als:

Hoek BAD + Hoek ABC + Hoek BCD + Hoek ADC = 360 graden.

Dit bewijst dat de som van de binnenhoeken van elke vierhoek altijd 360 graden is. Onthoud dit!

Verschillende Soorten Vierhoeken en Hun Eigenschappen

Hoewel de som van de hoeken altijd 360 graden is, hebben verschillende soorten vierhoeken verschillende eigenschappen met betrekking tot hun hoeken. Het is belangrijk om deze te kennen om specifieke problemen op te lossen.

Vierkant

Een vierkant is de meest regelmatige vierhoek. Alle zijden zijn even lang en alle hoeken zijn rechte hoeken (90 graden). Dus een vierkant heeft 4 hoeken van 90 graden, wat resulteert in een totale hoekensom van 4 * 90 = 360 graden.

Rechthoek

Een rechthoek heeft ook vier rechte hoeken (90 graden), maar de zijden hoeven niet allemaal even lang te zijn. Net als bij het vierkant, is de totale hoekensom 4 * 90 = 360 graden.

Parallellogram

Een parallellogram heeft twee paar evenwijdige zijden. De overstaande hoeken zijn gelijk. Dit betekent dat als één hoek x graden is, de tegenoverliggende hoek ook x graden is. De aangrenzende hoeken (hoeken die een zijde delen) zijn supplementair, wat betekent dat ze samen 180 graden zijn. Dus als één hoek x graden is, is de aangrenzende hoek (180 - x) graden.

Ruit

Een ruit (ook wel een rhombus genoemd) is een parallellogram met vier gelijke zijden. Net als bij het parallellogram zijn de overstaande hoeken gelijk en de aangrenzende hoeken supplementair. Echter, in tegenstelling tot een vierkant, zijn de hoeken van een ruit niet noodzakelijk rechte hoeken.

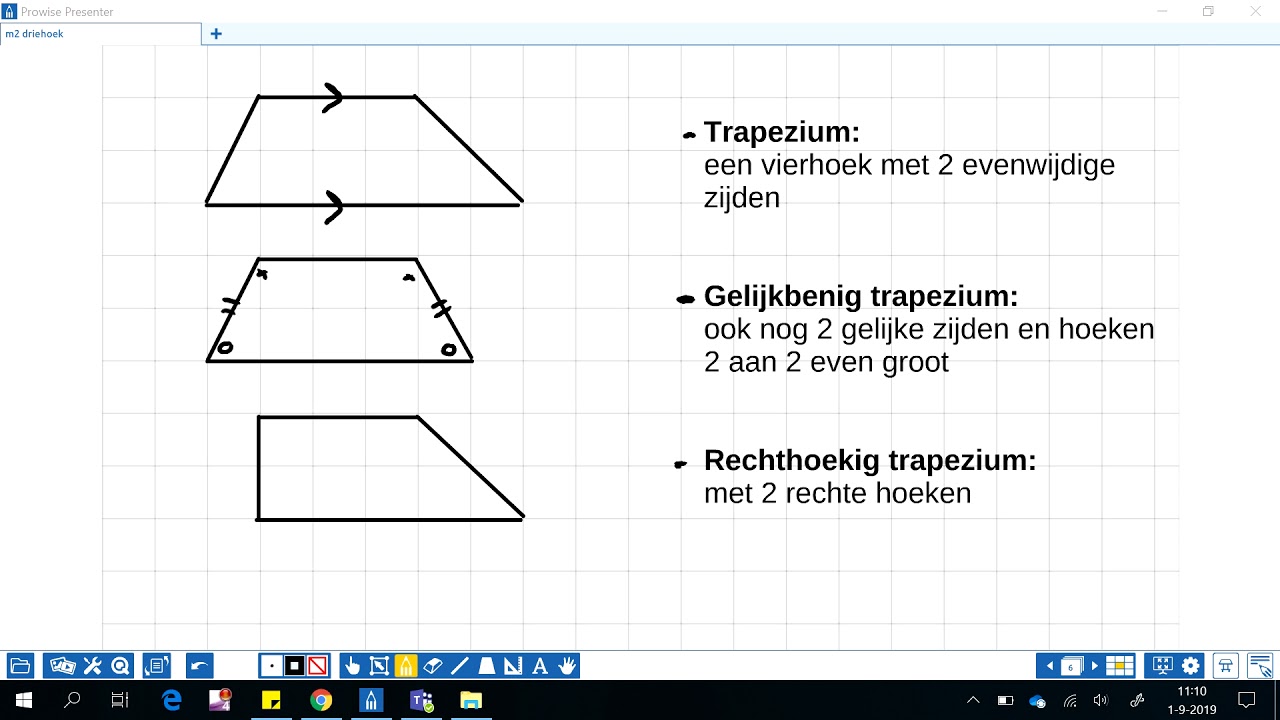
Trapezium (of Trapezoïde)

Een trapezium (in sommige regio's trapezoïde genoemd) heeft minstens één paar evenwijdige zijden. Er is geen algemene regel voor de individuele hoeken van een trapezium, behalve dat de hoeken aan dezelfde zijde tussen de evenwijdige lijnen supplementair zijn. Dus, als een trapezium AB // CD heeft, dan is Hoek A + Hoek D = 180 graden en Hoek B + Hoek C = 180 graden.

Vlieger

Een vlieger (of kite) heeft twee paar aangrenzende zijden die even lang zijn. De diagonalen van een vlieger staan loodrecht op elkaar. Eén paar overstaande hoeken is gelijk. De andere twee hoeken zijn niet noodzakelijk gelijk.

Praktische Voorbeelden en Toepassingen

Het begrijpen van de hoeken van vierhoeken is essentieel in veel praktische toepassingen. Denk aan architectuur, constructie en design.

• Architectuur: Architecten gebruiken de eigenschappen van vierhoeken bij het ontwerpen van gebouwen, ramen, deuren en andere structurele elementen. Zorg ervoor dat hoeken correct zijn, is cruciaal voor de stabiliteit en esthetiek van een gebouw.
• Constructie: In de constructie worden vierhoeken gebruikt bij het uitzetten van funderingen, het bouwen van muren en het installeren van dakbedekking. Precieze hoeken zijn belangrijk om ervoor te zorgen dat de constructie sterk en recht is.
• Design: Ontwerpers gebruiken vierhoeken bij het maken van patronen, logo's en andere grafische elementen. Het begrijpen van de hoeken van vierhoeken helpt hen om evenwichtige en aantrekkelijke ontwerpen te creëren.
• Navigatie: Kaarten en navigatie-instrumenten maken gebruik van vierhoeken om gebieden en afstanden weer te geven. Het begrijpen van de hoeken van vierhoeken helpt bij het bepalen van de juiste richting en afstand.

Voorbeeld: Stel dat je een parallellogram hebt waarbij één hoek 70 graden is. Omdat de overstaande hoeken gelijk zijn, is de tegenoverliggende hoek ook 70 graden. De andere twee hoeken zijn supplementair aan 70 graden, dus ze zijn elk 180 - 70 = 110 graden. De totale hoekensom is dus 70 + 70 + 110 + 110 = 360 graden.

Problemen Oplossen met de Hoekensom van een Vierhoek

De wetenschap dat de som van de hoeken in een vierhoek 360 graden is, kan gebruikt worden om onbekende hoeken te berekenen. Hier zijn een paar voorbeelden:

Voorbeeld 1: Je hebt een vierhoek ABCD, waarbij Hoek A = 80 graden, Hoek B = 100 graden en Hoek C = 90 graden. Wat is de grootte van Hoek D?

Oplossing: We weten dat Hoek A + Hoek B + Hoek C + Hoek D = 360 graden. Dus 80 + 100 + 90 + Hoek D = 360. Dit betekent dat 270 + Hoek D = 360, dus Hoek D = 360 - 270 = 90 graden.

Voorbeeld 2: Je hebt een trapezium met AB // CD. Hoek A = 60 graden. Wat is de grootte van Hoek D?

Oplossing: Aangezien AB // CD, weten we dat Hoek A + Hoek D = 180 graden. Dus 60 + Hoek D = 180. Dit betekent dat Hoek D = 180 - 60 = 120 graden.

Belangrijk: Het is essentieel om te weten welk type vierhoek je hebt, omdat de eigenschappen van de specifieke vierhoek je kunnen helpen bij het oplossen van het probleem.

Conclusie

Samenvattend is de som van de binnenhoeken van elke vierhoek altijd 360 graden. Dit fundamentele principe is een hoeksteen van de geometrie en heeft talloze toepassingen in de echte wereld. Door de verschillende soorten vierhoeken en hun specifieke eigenschappen te begrijpen, kun je problemen oplossen en de wereld om je heen beter begrijpen.

Dus de volgende keer dat je een vierkant, rechthoek, parallellogram, ruit, trapezium of vlieger ziet, onthoud dan: de som van de hoeken is 360 graden. Gebruik deze kennis om verder te kijken dan de basis en je geometrische vaardigheden verder te ontwikkelen. Oefening baart kunst! Probeer zelf verschillende vierhoeken te tekenen en hun hoeken te meten om je begrip te versterken. Veel succes!