Lengte Schuine Zijde Berekenen Met Graden

Heb je ooit naar een schuin dak gekeken en je afgevraagd hoe lang die hellende zijde eigenlijk is? Of misschien ben je een doe-het-zelver die een perfect passende plank moet snijden voor een project en heb je alleen de hoek en de hoogte? Dan ben je hier op de juiste plek. Het berekenen van de lengte van de schuine zijde (of hypotenusa) van een rechthoekige driehoek met behulp van graden is een vaardigheid die verrassend nuttig is in het dagelijks leven en in diverse professionele velden. We gaan het hier stap voor stap uitleggen, zodat je straks zelf aan de slag kunt.

Waarom zou je dit willen kunnen?

Laten we eerlijk zijn, wiskunde kan soms voelen als een ver-van-mijn-bed-show. Maar de realiteit is dat de principes van trigonometrie, zoals het berekenen van de schuine zijde, overal om ons heen te vinden zijn. Denk aan:

Bouwkunde en constructie: Een aannemer moet de lengte van een dakspant berekenen om materialen te bestellen.
Navigatie: Een zeeman gebruikt hoeken en afstanden om zijn positie te bepalen.
Engineering: Een ingenieur ontwerpt bruggen en gebouwen met behulp van trigonometrische principes om stabiliteit te garanderen.
Doe-het-zelf projecten: Je wilt een boekenplank ophangen met een bepaalde hellingshoek.

Zonder deze berekeningen zouden we letterlijk geen dak boven ons hoofd hebben, of veilige bruggen om over te steken. De impact van deze simpele wiskunde is dus enorm. Het is veel meer dan alleen een abstract concept; het is een praktische tool die we gebruiken om de wereld om ons heen te bouwen en te begrijpen.

De basis: De rechthoekige driehoek en Trigonometrie

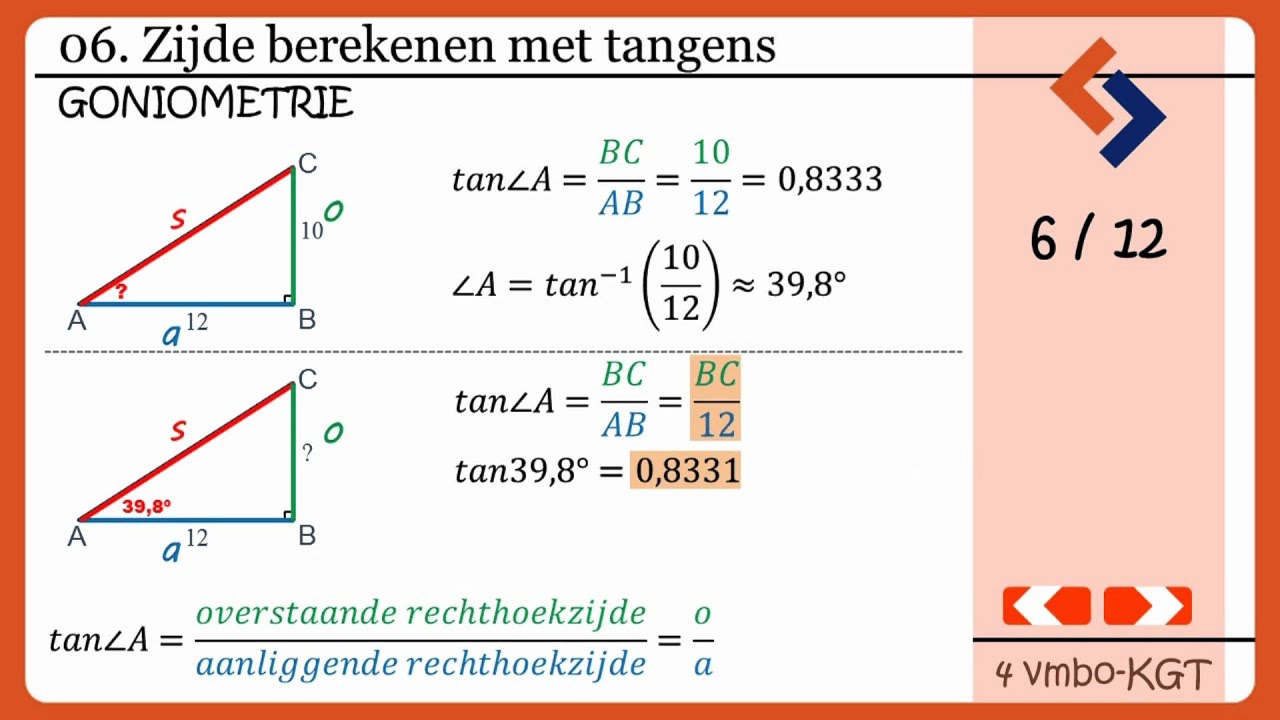
Alles begint met de rechthoekige driehoek. Dit is een driehoek met één hoek van 90 graden (een rechte hoek). De zijde tegenover de rechte hoek noemen we de schuine zijde (hypotenusa). De andere twee zijden noemen we de aanliggende en de overstaande zijde, afhankelijk van de hoek die we bekijken. Het is cruciaal dat je dit begrijpt voordat we verder gaan.

Trigonometrie is de tak van de wiskunde die zich bezighoudt met de relaties tussen de hoeken en de zijden van driehoeken. De belangrijkste trigonometrische functies zijn:

Sinus (sin): Overstaande zijde / Schuine zijde
Cosinus (cos): Aanliggende zijde / Schuine zijde
Tangens (tan): Overstaande zijde / Aanliggende zijde

Onthoud ze zo: SOS CAS TOA (Sinus = Overstaande / Schuine, Cosinus = Aanliggende / Schuine, Tangens = Overstaande / Aanliggende).

De formule om de schuine zijde te berekenen

Afhankelijk van welke gegevens je hebt (de hoek en de lengte van de aanliggende of overstaande zijde), kun je de volgende formules gebruiken:

* Als je de hoek (α) en de overstaande zijde (O) kent: sin(α) = O / S => S = O / sin(α) * Als je de hoek (α) en de aanliggende zijde (A) kent: cos(α) = A / S => S = A / cos(α)

Waar: * S = Lengte van de schuine zijde * α = De hoek in graden * O = Lengte van de overstaande zijde * A = Lengte van de aanliggende zijde

Een simpel voorbeeld

Stel, je hebt een rechthoekige driehoek met een hoek van 30 graden en de overstaande zijde is 5 cm lang. Wat is de lengte van de schuine zijde?

Gebruik de formule: S = O / sin(α)
Vul de waarden in: S = 5 cm / sin(30°)
Bereken sin(30°). De sinus van 30 graden is 0.5. (Gebruik een rekenmachine als je dit niet uit je hoofd weet!)
Deel 5 cm door 0.5: S = 5 cm / 0.5 = 10 cm

De schuine zijde is dus 10 cm lang!

Wat als je geen rekenmachine hebt?

Natuurlijk heb je niet altijd een rekenmachine bij de hand. In dat geval kun je:

Gebruik een online calculator: Er zijn talloze online trigonometrie calculators beschikbaar.
Gebruik een tabel met trigonometrische waarden: Deze tabellen geven de waarden van sinus, cosinus en tangens voor verschillende hoeken.
Schat de waarde: Voor sommige veelvoorkomende hoeken kun je de sinus- en cosinuswaarden uit je hoofd leren (zoals sin(30°) = 0.5). Voor andere hoeken kun je de waarde schatten op basis van je kennis van de eenheidscirkel.

Mogelijke valkuilen en hoe je ze vermijdt

Het berekenen van de schuine zijde lijkt eenvoudig, maar er zijn een paar dingen waar je op moet letten:

Zorg dat je rekenmachine in de juiste modus staat (graden of radialen): Een veelgemaakte fout is dat de rekenmachine in radialen staat terwijl je graden wilt gebruiken, of andersom. Controleer dit *altijd*!
Identificeer de juiste zijden: Weet je zeker dat je de overstaande en aanliggende zijde correct hebt geïdentificeerd ten opzichte van de gegeven hoek?
Rond correct af: Rond je antwoorden af naar een passend aantal decimalen, afhankelijk van de context van het probleem.

Tegenargumenten en misvattingen

Sommigen beweren dat dit soort wiskunde irrelevant is voor het "echte leven." Ze denken dat rekenmachines alles voor ons doen en dat we deze vaardigheden niet meer nodig hebben. Hoewel het waar is dat technologie ons leven gemakkelijker heeft gemaakt, is het belangrijk om te onthouden dat een goed begrip van de principes achter de technologie cruciaal is. Zonder dit begrip kunnen we de resultaten van een rekenmachine niet interpreteren of controleren op fouten.

Een andere misvatting is dat je een wiskundig genie moet zijn om dit te begrijpen. Dat is absoluut niet waar! Met een beetje oefening en de juiste uitleg kan *iedereen* de lengte van de schuine zijde berekenen.

Oefening baart kunst

De beste manier om deze vaardigheid te leren is door te oefenen. Hier zijn een paar oefenopgaven:

Een ladder staat onder een hoek van 70 graden tegen een muur. De voet van de ladder staat 2 meter van de muur. Hoe lang is de ladder?
Een kabel loopt van de top van een mast naar de grond. De hoek tussen de kabel en de grond is 55 graden. De mast is 10 meter hoog. Hoe lang is de kabel?
Een dak heeft een hellingshoek van 40 graden. De horizontale afstand van de dakrand tot de nok van het dak is 6 meter. Hoe lang is de dakspant?

Probeer deze opgaven zelf op te lossen. Kijk naar de oplossingen online als je er niet uitkomt. En wees niet bang om fouten te maken! Van fouten leer je het meest.

Samenvatting en volgende stappen

We hebben geleerd hoe je de lengte van de schuine zijde van een rechthoekige driehoek kunt berekenen met behulp van graden en trigonometrische functies. We hebben gezien hoe deze vaardigheid relevant is in verschillende praktische situaties, van bouw tot navigatie. We hebben ook enkele veelvoorkomende valkuilen besproken en hoe je ze kunt vermijden.

Nu je deze kennis hebt, is het tijd om verder te oefenen en je vaardigheden te verbeteren. Probeer verschillende soorten problemen op te lossen en daag jezelf uit. Je kunt ook online bronnen en tutorials raadplegen om je kennis verder uit te breiden.

Dus, welke interessante projecten of problemen kun je bedenken waarbij je deze nieuw verworven vaardigheid kunt toepassen? Ga aan de slag en ontdek de vele toepassingen van trigonometrie in de wereld om je heen!