Lorenz Curve And Gini Coefficient

Iedereen heeft een mening over de verdeling van rijkdom. Voelt het eerlijk? Zijn er immense verschillen of leven we in een maatschappij waar iedereen een gelijke kans heeft? De Lorenz-curve en de Gini-coëfficiënt zijn krachtige instrumenten die ons helpen om deze complexe vraagstukken te begrijpen en te visualiseren. Deze methoden, hoewel abstract, bieden concrete manieren om ongelijkheid te meten en te vergelijken, zowel binnen landen als tussen verschillende landen. Dit artikel is bedoeld voor een breed publiek, van studenten en beleidsmakers tot burgers die simpelweg nieuwsgierig zijn naar de economische krachten die onze wereld vormgeven.

Wat is de Lorenz-curve?

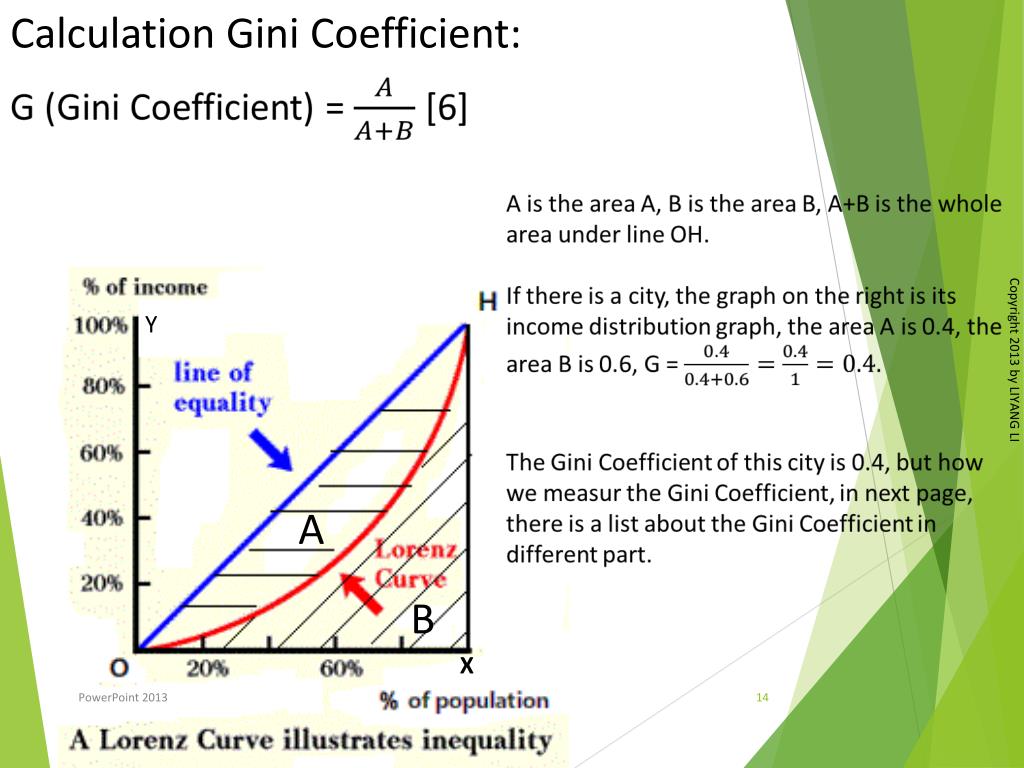
De Lorenz-curve is een grafische weergave van de inkomens- of vermogensverdeling in een bepaalde populatie. Het is een relatief eenvoudige maar uiterst effectieve manier om de mate van ongelijkheid te visualiseren. Stel je voor dat we alle huishoudens in een land rangschikken van arm naar rijk. Vervolgens tekenen we een grafiek waarin de cumulatieve percentage van de bevolking (horizontale as) wordt afgezet tegen de cumulatieve percentage van het totale inkomen of vermogen (verticale as).

Concreet:

• De horizontale as vertegenwoordigt het percentage van de bevolking, geordend van laagste naar hoogste inkomen/vermogen.
• De verticale as vertegenwoordigt het percentage van het totale inkomen/vermogen dat door dat deel van de bevolking wordt verdiend/bezeten.

De Lorenz-curve begint altijd in de oorsprong (0,0) en eindigt in het punt (100, 100). Waarom? Omdat 0% van de bevolking 0% van het inkomen/vermogen bezit, en 100% van de bevolking uiteraard 100% van het inkomen/vermogen bezit. De vorm van de curve geeft ons cruciale informatie over de verdeling.

De diagonaal: Perfecte gelijkheid

Een cruciale referentie in de Lorenz-curve is de diagonaal, een rechte lijn van de oorsprong naar het punt (100, 100). Deze lijn vertegenwoordigt perfecte gelijkheid. Stel je voor dat elk huishouden precies hetzelfde inkomen heeft. In dat geval zou 10% van de bevolking 10% van het inkomen verdienen, 50% van de bevolking 50% van het inkomen, en zo verder. De Lorenz-curve zou dan precies samenvallen met de diagonaal.

De kromming: Mate van ongelijkheid

In de praktijk is perfecte gelijkheid echter een utopie. De Lorenz-curve zal in de meeste gevallen onder de diagonaal liggen. Hoe verder de curve van de diagonaal afwijkt, hoe groter de ongelijkheid in de inkomens- of vermogensverdeling. Een curve die dicht bij de diagonaal ligt, duidt op een relatief gelijke verdeling, terwijl een curve die verder weg ligt op een ongelijker verdeling wijst.

Stel je voor dat de onderste 20% van de bevolking slechts 5% van het totale inkomen verdient. De Lorenz-curve zou dan onder de diagonaal liggen. Als de onderste 20% daarentegen 10% van het totale inkomen verdient, ligt de curve dichter bij de diagonaal en is de ongelijkheid minder groot.

De Gini-coëfficiënt: Een numerieke samenvatting

Hoewel de Lorenz-curve een krachtige visuele weergave biedt, is het vaak handig om de ongelijkheid te kwantificeren met een enkel getal. Hier komt de Gini-coëfficiënt om de hoek kijken. De Gini-coëfficiënt is een numerieke maatstaf van ongelijkheid, gebaseerd op de Lorenz-curve. Het is een getal tussen 0 en 1 (soms uitgedrukt als een percentage tussen 0 en 100).

De Gini-coëfficiënt wordt berekend als de oppervlakte tussen de diagonaal van perfecte gelijkheid en de Lorenz-curve, gedeeld door de totale oppervlakte onder de diagonaal. Met andere woorden:

Gini-coëfficiënt = (Oppervlakte tussen diagonaal en Lorenz-curve) / (Oppervlakte onder de diagonaal)

Laten we de interpretatie van de Gini-coëfficiënt bekijken:

• Gini = 0: Perfecte gelijkheid. Iedereen heeft hetzelfde inkomen/vermogen. De Lorenz-curve valt samen met de diagonaal.
• Gini = 1: Perfecte ongelijkheid. Eén persoon bezit al het inkomen/vermogen, en de rest heeft niets. De Lorenz-curve valt samen met de horizontale as tot het laatste punt, waarna hij verticaal omhoog schiet naar (100, 100).
• 0 < Gini < 1: Een waarde tussen 0 en 1 duidt op een mate van ongelijkheid. Hoe hoger de Gini-coëfficiënt, hoe groter de ongelijkheid.

Een land met een Gini-coëfficiënt van 0,2 zou dus een veel egalere inkomensverdeling hebben dan een land met een Gini-coëfficiënt van 0,6.

Voorbeelden van Gini-coëfficiënten wereldwijd

De Gini-coëfficiënten variëren aanzienlijk tussen landen. Scandinavische landen, zoals Denemarken en Zweden, hebben doorgaans lage Gini-coëfficiënten (rond de 0,25-0,30), wat duidt op een relatief gelijke inkomensverdeling. Aan de andere kant van het spectrum bevinden zich landen in Afrika en Latijns-Amerika, waar de Gini-coëfficiënten vaak boven de 0,50 liggen, wat wijst op een hoge mate van ongelijkheid. De Verenigde Staten bevinden zich ergens in het midden, met een Gini-coëfficiënt die historisch gezien hoger is dan die van de meeste andere ontwikkelde landen, maar lager dan die van veel ontwikkelingslanden.

Waarom zijn de Lorenz-curve en de Gini-coëfficiënt belangrijk?

Het begrijpen van inkomens- en vermogensverdeling is cruciaal om verschillende redenen:

• Sociale rechtvaardigheid: Veel mensen vinden dat een eerlijke verdeling van rijkdom essentieel is voor een rechtvaardige samenleving. De Lorenz-curve en de Gini-coëfficiënt helpen ons te beoordelen in hoeverre een samenleving daadwerkelijk rechtvaardig is.
• Economische stabiliteit: Extreme ongelijkheid kan leiden tot economische instabiliteit. Een grote kloof tussen arm en rijk kan leiden tot sociale onrust, verminderde consumptie en belemmering van economische groei.
• Beleidsvorming: De Lorenz-curve en de Gini-coëfficiënt bieden beleidsmakers waardevolle informatie om beleid te ontwikkelen dat gericht is op het verminderen van ongelijkheid. Dit kan bijvoorbeeld via progressieve belastingheffing, sociale zekerheidsprogramma's en investeringen in onderwijs en gezondheidszorg.
• Internationale vergelijking: Deze instrumenten stellen ons in staat om de inkomensverdeling tussen verschillende landen te vergelijken. Dit kan inzicht geven in de effectiviteit van verschillende beleidsmaatregelen en economische systemen.

Kritiek op de Gini-coëfficiënt

Hoewel de Gini-coëfficiënt een veelgebruikte en nuttige maatstaf is, is het belangrijk om ook de beperkingen te erkennen:

• Verlies van detail: De Gini-coëfficiënt is een samenvattende maatstaf en kan informatie over de specifieke vorm van de inkomensverdeling verbergen. Twee landen met dezelfde Gini-coëfficiënt kunnen toch een zeer verschillende inkomensverdeling hebben.
• Gevoeligheid voor uitersten: De Gini-coëfficiënt is relatief gevoelig voor veranderingen in het midden van de inkomensverdeling en minder gevoelig voor veranderingen aan de uiteinden (de allerarmsten en de allerrijksten).
• Geen rekening met welvaart: De Gini-coëfficiënt meet alleen de relatieve ongelijkheid, niet het absolute welvaartsniveau. Een land met een hoge Gini-coëfficiënt kan toch een hoger algemeen welvaartsniveau hebben dan een land met een lage Gini-coëfficiënt.
• Data kwaliteit: De betrouwbaarheid van de Gini-coëfficiënt is afhankelijk van de kwaliteit van de beschikbare inkomens- en vermogensgegevens. In sommige landen zijn deze gegevens mogelijk onvolledig of onnauwkeurig.

Hoe kunnen we de Lorenz-curve en Gini-coëfficiënt gebruiken in ons dagelijks leven?

Hoewel de Lorenz-curve en de Gini-coëfficiënt misschien abstract lijken, kunnen ze ons helpen om kritischer na te denken over de economische realiteit om ons heen.

• Nieuwsberichten interpreteren: Als je een nieuwsbericht leest over de economie, probeer dan kritisch na te denken over hoe de inkomensverdeling eruit zou kunnen zien. Zou de Lorenz-curve dicht bij de diagonaal liggen, of er ver vanaf? Welke implicaties heeft dit voor de sociale rechtvaardigheid en economische stabiliteit?
• Politieke debatten analyseren: Politici debatteren vaak over economisch beleid. Probeer te beoordelen welke beleidsvoorstellen de inkomensverdeling waarschijnlijk gelijker zouden maken, en welke de ongelijkheid zouden vergroten.
• Bewustwording creëren: Praat met vrienden en familie over inkomensongelijkheid. Deel je kennis over de Lorenz-curve en de Gini-coëfficiënt en moedig anderen aan om ook kritisch na te denken over deze belangrijke kwestie.

Het is belangrijk om te onthouden dat economie niet alleen over cijfers gaat, maar ook over mensen. De Lorenz-curve en de Gini-coëfficiënt zijn hulpmiddelen die ons kunnen helpen om een beter begrip te krijgen van de economische krachten die onze levens beïnvloeden. Door deze instrumenten te gebruiken, kunnen we beter geïnformeerde burgers worden en een bijdrage leveren aan een meer rechtvaardige en welvarende samenleving voor iedereen.

Conclusie

De Lorenz-curve en de Gini-coëfficiënt zijn essentiële instrumenten voor het begrijpen en kwantificeren van inkomens- en vermogensongelijkheid. Hoewel ze hun beperkingen hebben, bieden ze een waardevol perspectief op de verdeling van rijkdom binnen een samenleving. Door deze tools te begrijpen, kunnen we beter geïnformeerde discussies voeren over beleid dat gericht is op het verminderen van ongelijkheid en het bevorderen van een rechtvaardiger en welvarender wereld voor iedereen. We moedigen je aan om verder te onderzoeken en je eigen conclusies te trekken over de cruciale kwestie van economische gelijkheid.