Oppervlakte Van Een Trapezium Berekenen

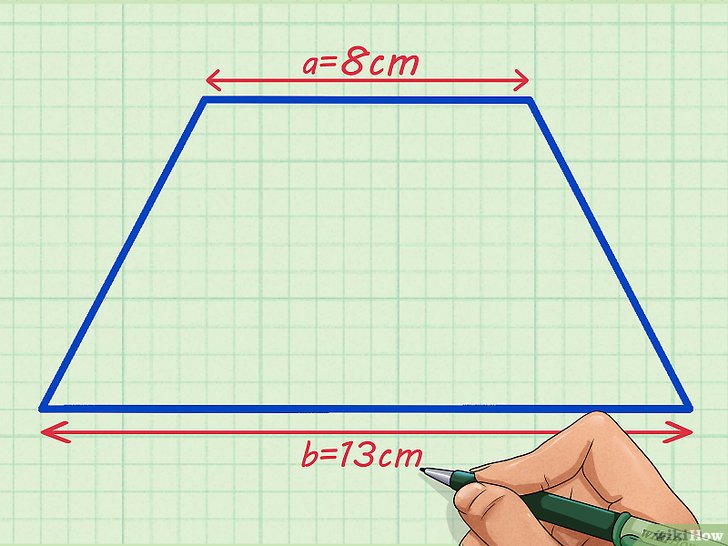
Ken je dat moment dat je naar een vorm kijkt en je je afvraagt: "Hoe bereken ik hier nou de oppervlakte van?" Het overkomt ons allemaal, zeker bij vormen die niet zo alledaags zijn als een vierkant of een cirkel. Eén van die vormen is het trapezium, ook wel trapezoïde genoemd. Geen paniek! Het is makkelijker dan je denkt. In dit artikel ga ik je stap voor stap uitleggen hoe je de oppervlakte van een trapezium berekent, en waarom dat in de echte wereld eigenlijk best handig kan zijn.

Waarom Zou Je de Oppervlakte van een Trapezium Willen Berekenen?

Oké, eerlijk is eerlijk, niet iedereen heeft dagelijks een trapezium voor zich liggen. Maar denk eens aan:

Tuinieren: Misschien heeft je tuin een border in de vorm van een trapezium. Wil je weten hoeveel aarde je nodig hebt? Oppervlakte berekenen!
Bouw en constructie: Daken, bruggen, gevels – vaak zitten er trapeziumvormige elementen in.
Kunst en design: Een kunstenaar die een mozaïek maakt, of een designer die een meubelstuk ontwerpt, kan te maken krijgen met trapezia.
Wiskunde zelf: Natuurlijk is het ook gewoon een belangrijke skill om te hebben, vooral als je verder gaat in de wiskunde.

Het gaat er dus niet alleen om de formule uit je hoofd te leren. Het gaat erom dat je een stukje gereedschap in handen hebt waarmee je de wereld om je heen beter kunt begrijpen. En wie weet, misschien kom je het nog eens tegen als je een spelletje speelt of een puzzel oplost!

Wat Is een Trapezium Eigenlijk?

Laten we even terug naar de basis gaan. Een trapezium is een vierhoek (een figuur met vier zijden) met minstens één paar evenwijdige zijden. Deze evenwijdige zijden noemen we de basissen (basis 1 en basis 2), en de afstand tussen deze twee basissen noemen we de hoogte. Let op: de hoogte staat altijd loodrecht op de basissen.

Er zijn verschillende soorten trapezia:

Gelijkbenig trapezium: De niet-evenwijdige zijden zijn even lang.
Rechthoekig trapezium: Minstens één van de niet-evenwijdige zijden staat loodrecht op de basissen.
Onregelmatig trapezium: Geen bijzondere eigenschappen, behalve dat er één paar evenwijdige zijden is.

Gelukkig is de formule voor de oppervlakte voor alle soorten trapezia hetzelfde.

De Formule voor de Oppervlakte van een Trapezium

Hier komt ie: de formule is:

Oppervlakte = (basis 1 + basis 2) / 2 * hoogte

Of, in kortere notatie:

A = ((b1 + b2) / 2) * h

Waarbij:

A staat voor de oppervlakte.
b1 staat voor de lengte van de eerste basis.
b2 staat voor de lengte van de tweede basis.
h staat voor de hoogte.

Het komt erop neer dat je het gemiddelde van de twee basissen neemt, en dat vermenigvuldigt met de hoogte. Simpel toch?

Stap voor Stap: Hoe Bereken Je de Oppervlakte?

Laten we een voorbeeld bekijken om het helemaal duidelijk te maken.

Stap 1: Identificeer de basissen en de hoogte. Stel, we hebben een trapezium met de volgende afmetingen:

Basis 1 (b1) = 8 cm
Basis 2 (b2) = 12 cm
Hoogte (h) = 5 cm

Stap 2: Vul de formule in. We plaatsen de waarden in de formule:

A = ((8 + 12) / 2) * 5

Stap 3: Bereken de oppervlakte. We lossen de vergelijking op:

8 + 12 = 20
20 / 2 = 10
10 * 5 = 50

Dus, de oppervlakte van het trapezium is 50 cm² (vierkante centimeter). Vergeet de eenheid niet!

Nog een voorbeeld

Laten we een iets lastiger voorbeeld doen. Stel, je hebt een trapezium waarbij de hoogte niet direct gegeven is, maar je wel andere informatie hebt waardoor je de hoogte kunt berekenen (bijvoorbeeld met de stelling van Pythagoras). De basissen zijn 6 meter en 10 meter. De niet-evenwijdige zijden zijn 5 meter lang, en het is een gelijkbenig trapezium.

Om de hoogte te vinden, trekken we een loodlijn van de bovenste basis (6 meter) naar de onderste basis (10 meter). Omdat het een gelijkbenig trapezium is, is de afstand van de voet van de loodlijn tot de hoekpunten van de onderste basis aan beide kanten gelijk aan (10 - 6)/2 = 2 meter.

Nu hebben we een rechthoekige driehoek met een hypotenusa van 5 meter en een zijde van 2 meter. Met de stelling van Pythagoras (a² + b² = c²) kunnen we de hoogte (b) berekenen:

2² + b² = 5²
4 + b² = 25
b² = 21
b = √21 ≈ 4.58 meter

Nu we de hoogte hebben, kunnen we de oppervlakte berekenen:

A = ((6 + 10) / 2) * 4.58
A = (16 / 2) * 4.58
A = 8 * 4.58
A ≈ 36.64 m²

De oppervlakte van dit trapezium is dus ongeveer 36.64 vierkante meter.

Waar Moet Je Op Letten?

Een paar belangrijke punten om te onthouden:

De hoogte moet loodrecht staan op de basissen. Soms is de hoogte niet direct gegeven, maar moet je deze eerst berekenen met bijvoorbeeld de stelling van Pythagoras.
Zorg dat je dezelfde eenheden gebruikt. Als de basissen in centimeters zijn, moet de hoogte ook in centimeters zijn. De oppervlakte is dan in vierkante centimeters (cm²).
Verwar de basissen niet met de andere zijden. De basissen zijn de evenwijdige zijden.

Zijn Er Andere Manieren Om de Oppervlakte te Berekenen?

Ja, er zijn alternatieve methoden, al zijn die vaak complexer:

Verdelen in rechthoeken en driehoeken: Je kunt een trapezium opsplitsen in een rechthoek en een of twee driehoeken. Bereken de oppervlakte van elk van deze vormen en tel ze bij elkaar op. Dit is vooral handig bij onregelmatige trapezia.
Met behulp van integralen (hogere wiskunde): In de calculus kun je de oppervlakte onder een functie berekenen met behulp van integralen. Als je de functie kent die de vorm van het trapezium beschrijft, kun je de oppervlakte op deze manier bepalen.

Maar over het algemeen is de formule die we hierboven hebben besproken de snelste en meest efficiënte manier.

Counterpoints: Is Het Echt Zo Belangrijk Om Dit Te Weten?

Sommige mensen zullen zeggen: "Wanneer ga ik dit in het echt ooit gebruiken? Ik heb toch een rekenmachine?" Dat is een begrijpelijke vraag. Het is waar dat je niet elke dag de oppervlakte van een trapezium zult hoeven berekenen. Maar het gaat om meer dan alleen het uitrekenen van een getal.

Het leren van wiskunde, en in dit geval het begrijpen van meetkunde, scherpt je analytisch denkvermogen. Het leert je probleemoplossend te denken. En dat zijn vaardigheden die je in alle aspecten van je leven kunt gebruiken, of het nu op je werk is, bij het organiseren van je huis, of bij het nemen van belangrijke beslissingen.

Bovendien, zoals ik eerder al zei, kan het handig zijn bij bepaalde hobby's of projecten. En wie weet, misschien inspireert het je wel om verder te gaan in de wiskunde of in een technisch beroep!

Samenvatting en Actie

We hebben gezien dat het berekenen van de oppervlakte van een trapezium eigenlijk heel eenvoudig is. Je hoeft alleen maar de formule te onthouden: A = ((b1 + b2) / 2) * h, de waarden correct in te vullen, en de berekening uit te voeren.

Probeer het nu zelf! Pak een pen en papier, teken een aantal trapezia met verschillende afmetingen, en bereken de oppervlakte. Of zoek in je omgeving naar objecten die de vorm hebben van een trapezium en probeer de oppervlakte te schatten. Hoe meer je oefent, hoe beter je het zult begrijpen.

Heb je nog vragen? Laat dan een reactie achter! En vergeet niet: wiskunde is niet eng, het is gewoon een taal die je moet leren spreken.

Ben je nu nieuwsgierig naar andere geometrische vormen? Welke vorm wil je dat we de volgende keer behandelen?