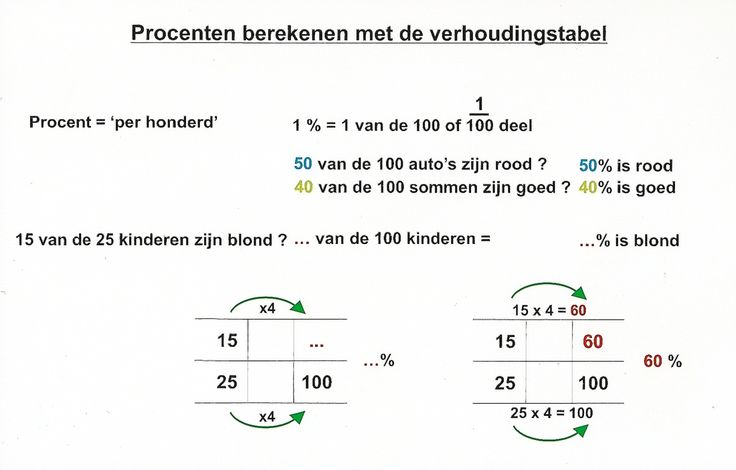
Percentage Berekenen Tussen 2 Getallen

Herken je dat? Je zit te puzzelen met cijfers, probeert te begrijpen hoeveel korting je nu écht krijgt, of wilt weten hoeveel procent van je team de deadline heeft gehaald. Procenten berekenen tussen twee getallen kan soms voelen als een wiskundig doolhof. Je bent zeker niet de enige die hier af en toe mee worstelt. Het is een vaardigheid die, hoewel vaak aangeleerd op school, in de praktijk soms lastiger blijkt dan gedacht. Deze artikel is er om die doolhof te verhelderen en je de tools te geven om zelfverzekerd met percentages aan de slag te gaan.

Waarom is dit belangrijk?

Procenten zijn overal. Denk aan:

Korting: "25% korting! Maar hoeveel euro is dat nu eigenlijk?"
Rente: "Hoeveel rente krijg ik op mijn spaarrekening?"
Statistieken: "Welk percentage van de bevolking heeft gestemd?"
Prestaties: "Hoeveel procent van de projecten zijn op tijd afgerond?"
Verandering: "Met hoeveel procent is de omzet gestegen?"

Het begrijpen en kunnen berekenen van percentages stelt je in staat om geïnformeerde beslissingen te nemen, zowel in je persoonlijke leven als in je professionele carrière. Het geeft je de controle over je eigen financiën, helpt je prestaties te analyseren en stelt je in staat om kritisch naar informatie te kijken. Kortom, het is een cruciale vaardigheid voor iedereen.

De basisformule: Hoe bereken je het?

De basisformule voor het berekenen van het percentage tussen twee getallen is eigenlijk heel simpel:

(Deel / Geheel) * 100 = Percentage

Laten we dit ontleden:

Deel: Dit is het getal waarvan je wilt weten hoeveel procent het is.
Geheel: Dit is het totale getal, de basis waar je vanuit rekent.
Percentage: Dit is het resultaat van de berekening, uitgedrukt in procenten.

Voorbeeld: Stel je hebt 50 appels. 10 daarvan zijn rot. Welk percentage van de appels is rot?

Deel: 10 (de rotte appels)
Geheel: 50 (het totaal aantal appels)

(10 / 50) * 100 = 20%

Dus, 20% van de appels is rot.

Verschillende scenario's en voorbeelden

De basisformule is handig, maar de context kan variëren. Laten we een paar veelvoorkomende scenario's bekijken:

1. Korting berekenen

Stel, een product kost €100 en je krijgt 20% korting. Hoeveel betaal je dan?

Eerst berekenen we de korting in euro's:

(20 / 100) * 100 = €20 korting

Vervolgens trekken we de korting af van de originele prijs:

€100 - €20 = €80

Je betaalt dus €80 voor het product.

2. Percentage van een toename berekenen

Stel, je salaris was vorig jaar €2000 en dit jaar €2200. Met hoeveel procent is je salaris gestegen?

Eerst berekenen we het verschil:

€2200 - €2000 = €200

Vervolgens delen we het verschil door het originele salaris:

€200 / €2000 = 0.1

En vermenigvuldigen we dit met 100 om het percentage te krijgen:

0.1 * 100 = 10%

Je salaris is met 10% gestegen.

3. Percentage van een afname berekenen

Stel, een aandeel was €50 waard en is nu €40 waard. Met hoeveel procent is de waarde gedaald?

Eerst berekenen we het verschil:

€50 - €40 = €10

Vervolgens delen we het verschil door de originele waarde:

€10 / €50 = 0.2

En vermenigvuldigen we dit met 100 om het percentage te krijgen:

0.2 * 100 = 20%

De waarde van het aandeel is met 20% gedaald.

Veelgemaakte fouten en hoe ze te vermijden

Het lijkt simpel, maar er sluipen vaak fouten in bij het berekenen van percentages. Hier zijn een paar valkuilen:

Verkeerde basis: Gebruik altijd de juiste waarde als 'geheel'. Bij een salarisstijging is het oude salaris de basis, niet het nieuwe.
Decimalen negeren: Rond niet te vroeg af. Behoud voldoende decimalen tijdens de berekening en rond pas af op het einde.
Procentpunten en percentages verwarren: Een stijging van 10% naar 12% is een stijging van 2 procentpunten, maar een stijging van 20% (2/10 * 100).
Logica vergeten: Controleer altijd of het resultaat logisch is. Als een product duurder is geworden, kan de korting nooit hoger zijn dan 100%.

Tegenargumenten: Is er een alternatieve manier?

Hoewel de basisformule altijd werkt, zijn er alternatieve manieren om percentages te berekenen, afhankelijk van de situatie. Bijvoorbeeld, als je de percentage wilt toevoegen aan een getal, kun je het getal vermenigvuldigen met (1 + percentage/100). Echter, de basisformule blijft de meest universele en gemakkelijk te begrijpen methode.

Sommige mensen vertrouwen liever op online calculators. Dit is zeker een optie, maar het is belangrijk om de basisprincipes te begrijpen, zodat je de resultaten kunt controleren en begrijpen. Daarnaast ben je niet altijd in de gelegenheid om een calculator te gebruiken.

Tools en hulpmiddelen

Er zijn veel tools beschikbaar die je kunnen helpen met het berekenen van percentages:

Rekenmachines: Standaard rekenmachines hebben een procentknop.
Spreadsheets (Excel, Google Sheets): Bieden speciale functies voor het berekenen van percentages.
Online Percentage Calculators: Er zijn talloze websites en apps die je kunt gebruiken.

Maar onthoud, de beste tool is je eigen begrip van de basisprincipes.

De impact in de praktijk

Stel je voor: je bent ondernemer en je wilt de effectiviteit van een marketingcampagne meten. Door percentages te berekenen, kun je precies zien hoeveel de verkoop is gestegen dankzij de campagne. Je kunt ook de conversieratio van je website analyseren en bepalen welke pagina's verbetering behoeven. Dit zijn cruciale inzichten die je helpen om betere beslissingen te nemen en je bedrijf te laten groeien.

Ook in je dagelijkse leven is het handig. Je vergelijkt aanbiedingen in de supermarkt en berekent welke deal het voordeligst is. Of je plant een vakantie en wilt weten hoeveel procent van je budget al is uitgegeven. Met de juiste kennis van percentages ben je financieel slimmer en kun je beter plannen.

Conclusie

Het berekenen van percentages tussen twee getallen is een essentiële vaardigheid die je helpt om geïnformeerde beslissingen te nemen en de wereld om je heen beter te begrijpen. Hoewel het in eerste instantie misschien ingewikkeld lijkt, is de basisformule eenvoudig en gemakkelijk toe te passen. Door de basisprincipes te begrijpen en veel te oefenen, kun je zelfverzekerd met percentages aan de slag gaan.

Dus, ben je klaar om je rekenvaardigheden in de praktijk te brengen en de controle over je cijfers te nemen? Welke situatie ga jij als eerste aanpakken met je nieuwe kennis over percentages?