Rekenen Met Breuken Groep 8

Hallo allemaal! Zit je in groep 8 en vind je rekenen met breuken soms lastig? Je bent zeker niet de enige! Veel leerlingen worstelen met dit onderwerp. Het voelt misschien alsof je verdwaalt in een woud van getallen en streepjes, maar geloof me, met de juiste uitleg en wat oefening, wordt het een stuk duidelijker. Laten we samen ontdekken hoe breuken werken en hoe je ze kunt gebruiken.

Waarom Breuken Zo Belangrijk Zijn

Misschien denk je nu: "Waarom moet ik dit eigenlijk leren? Wanneer gebruik ik dit later?". Dat is een goede vraag! Breuken zijn overal om je heen, ook al zie je het niet direct. Denk maar eens aan:

• Koken: Een half kopje bloem, een kwart theelepel zout. Recepten zitten vol breuken!
• Sport: Je speelt een half uur voetbal of rent een kwart van de marathon.
• Tijd: Een kwartier wachten, een halve dag vrij.
• Delen: Je deelt een pizza met vrienden. Iedereen krijgt een deel, een breuk van de pizza.

Begrijp je breuken, dan begrijp je een groot deel van de wereld om je heen. Bovendien is het een belangrijke basis voor de wiskunde die je later op de middelbare school krijgt. Het is dus echt de moeite waard om hier even goed in te duiken!

Wat Maakt Breuken Zo Moeilijk?

Het probleem met breuken zit vaak in het abstracte karakter ervan. Het is niet altijd makkelijk om je voor te stellen wat een breuk nu precies betekent. En dan zijn er ook nog al die regels: gelijknamig maken, vereenvoudigen, vermenigvuldigen... Het kan overweldigend zijn.

Soms hoor je mensen zeggen: "Ach, breuken, dat is toch gewoon een kwestie van regels uit je hoofd leren?". Maar dat is niet de beste aanpak. Begrijpen wat je doet is veel belangrijker dan alleen maar regels onthouden. Als je de basis begrijpt, kun je de regels zelf bedenken en ze beter onthouden.

De Basis: Wat Is Een Breuk Eigenlijk?

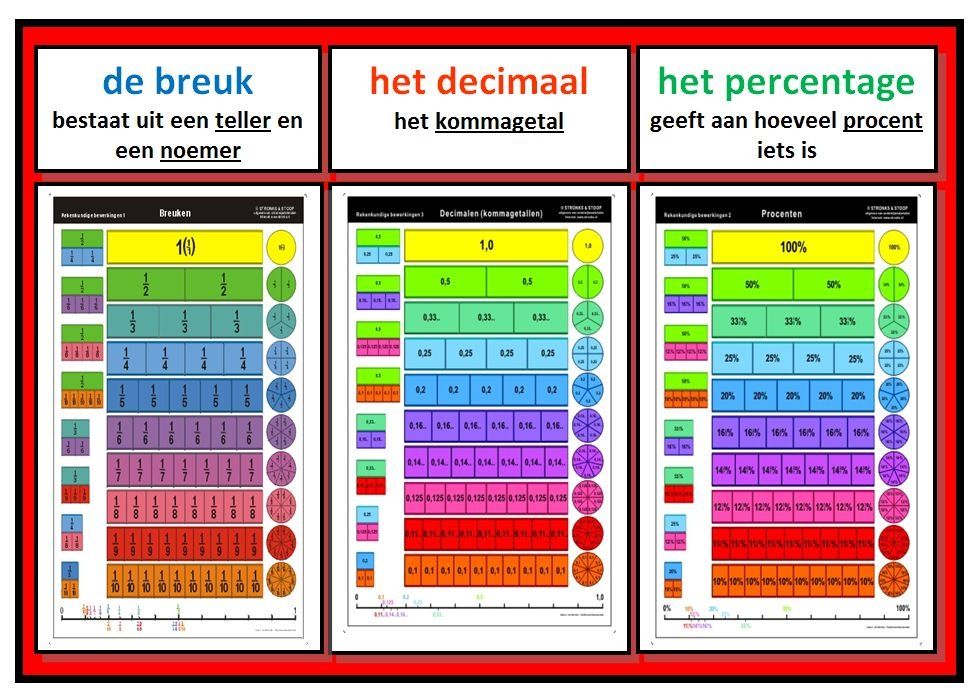
Een breuk is eigenlijk niets meer dan een deel van een geheel. Stel je voor: je hebt een taart. Die taart is het geheel. Als je de taart in vier gelijke stukken snijdt, is elk stukje ¹/₄ van de taart. De 1 noemen we de teller (het aantal stukken dat je hebt) en de 4 noemen we de noemer (het totale aantal stukken waarin de taart verdeeld is).

Denk aan een pizza. Als je ³/₈ van de pizza opeet, betekent dat dat de pizza in 8 stukken verdeeld was en jij er 3 van hebt opgegeten.

Soorten Breuken

• Echte breuk: De teller is kleiner dan de noemer (bijvoorbeeld ²/₅).
• Onechte breuk: De teller is groter dan of gelijk aan de noemer (bijvoorbeeld ⁵/₃).
• Gemengde breuk: Een combinatie van een heel getal en een breuk (bijvoorbeeld 1 ²/₃).

Rekenen Met Breuken: De Basisprincipes

Nu we weten wat een breuk is, kunnen we gaan rekenen. Hieronder de belangrijkste bewerkingen:

Breuken Gelijknamig Maken

Om breuken op te tellen of af te trekken, moeten ze gelijknamig zijn. Dat betekent dat ze dezelfde noemer moeten hebben. Hoe doe je dat?

Voorbeeld: Je wilt ¹/₂ + ¹/₃ uitrekenen.

1. Zoek de kleinste gemene veelvoud (KGV) van de noemers (2 en 3). De KGV van 2 en 3 is 6.
2. Maak beide breuken gelijknamig met noemer 6.
   • ¹/₂ = ³/₆ (teller en noemer vermenigvuldigd met 3)
   • ¹/₃ = ²/₆ (teller en noemer vermenigvuldigd met 2)

Breuken Optellen en Aftrekken

Als de breuken gelijknamig zijn, is optellen en aftrekken simpel: je telt (of trekt) alleen de tellers op (of af). De noemer blijft hetzelfde.

Voorbeeld: ³/₆ + ²/₆ = ⁵/₆

Voorbeeld: ⁵/₈ - ²/₈ = ³/₈

Breuken Vermenigvuldigen

Breuken vermenigvuldigen is eigenlijk heel makkelijk: teller keer teller, noemer keer noemer.

Voorbeeld: ²/₃ x ¹/₄ = ^{2 x 1}/_{3 x 4} = ²/₁₂. Je kunt deze breuk nog vereenvoudigen tot ¹/₆.

Breuken Delen

Breuken delen lijkt misschien ingewikkeld, maar er is een simpele truc: vermenigvuldig met het omgekeerde.

Voorbeeld: ¹/₂ : ¹/₄. Het omgekeerde van ¹/₄ is ⁴/₁ (of gewoon 4).

Dus: ¹/₂ : ¹/₄ = ¹/₂ x ⁴/₁ = ⁴/₂ = 2

Breuken Vereenvoudigen

Een breuk is vereenvoudigd als de teller en de noemer geen gemeenschappelijke delers meer hebben (behalve 1). Je deelt dus zowel de teller als de noemer door hetzelfde getal tot je niet verder kunt.

Voorbeeld: ⁴/₈. Zowel 4 als 8 zijn deelbaar door 4. Dus: ⁴/₈ = ¹/₂

Tips en Trucs voor Breuken

• Visualiseer: Teken cirkels, rechthoeken of andere vormen en verdeel ze in stukken om de breuken te zien.
• Oefening baart kunst: Maak veel oefenopgaven. Hoe meer je oefent, hoe beter je het gaat begrijpen.
• Vraag om hulp: Als je iets niet begrijpt, vraag dan je leraar, ouders of een vriend(in) om hulp.
• Gebruik online hulpmiddelen: Er zijn veel websites en apps die je kunnen helpen met breuken.
• Maak het leuk: Zoek spelletjes of activiteiten waarbij je breuken kunt gebruiken.

Omgaan Met Lastige Vragen

Soms kom je vragen tegen die extra lastig lijken. Bijvoorbeeld:

"Jan heeft ²/₃ van een pizza gegeten. Marieke heeft ¹/₄ van de pizza gegeten. Hoeveel hebben ze samen gegeten?"

Hier is het belangrijk om stap voor stap te werken:

1. Wat wordt er gevraagd? Hoeveel hebben ze samen gegeten?
2. Welke informatie heb je? Jan at ²/₃, Marieke at ¹/₄.
3. Welke bewerking moet je doen? Optellen.
4. Los de som op: ²/₃ + ¹/₄ = ⁸/₁₂ + ³/₁₂ = ¹¹/₁₂

Dus, Jan en Marieke hebben samen ¹¹/₁₂ van de pizza gegeten.

Het Belang van een Positieve Mindset

Het is heel belangrijk om niet op te geven als het even moeilijk is. Iedereen maakt fouten. Van fouten kun je leren. Blijf positief en geef niet op, en je zult zien dat je steeds beter wordt in rekenen met breuken.

Geloof in jezelf! Met de juiste instelling en de juiste hulpmiddelen kan iedereen leren rekenen met breuken.

Een Ander Perspectief: Breuken Als Verhoudingen

Soms is het handig om breuken te zien als verhoudingen. Een breuk kan dan aangeven hoe iets zich verhoudt tot iets anders. Bijvoorbeeld:

"In een klas zitten 12 jongens en 18 meisjes. Welke breuk van de klas bestaat uit jongens?"

Eerst berekenen we het totaal aantal leerlingen: 12 + 18 = 30

De breuk die de verhouding jongens aangeeft is dan ¹²/₃₀. Deze breuk kunnen we vereenvoudigen tot ²/₅.

Dus ²/₅ van de klas bestaat uit jongens. Dit perspectief kan helpen om breuken in een andere context te zien en beter te begrijpen.

De Toekomst Met Breuken

Zoals we al eerder zeiden, breuken zijn overal. En ze zullen ook in de toekomst belangrijk blijven. Of je nu ingenieur, kok, architect, of iets heel anders wilt worden, een goed begrip van breuken zal je zeker van pas komen.

Dus, wees niet bang voor breuken! Zie ze als een uitdaging, een puzzel die je kunt oplossen. En onthoud: oefening baart kunst!

Nu je dit gelezen hebt, ben je al een stuk verder! Wat ga jij nu doen om je breuken skills verder te verbeteren? Ga je oefenopgaven maken, een spelletje spelen, of iemand om hulp vragen? Succes!