Schuine Zijde Berekenen Van Een Driehoek

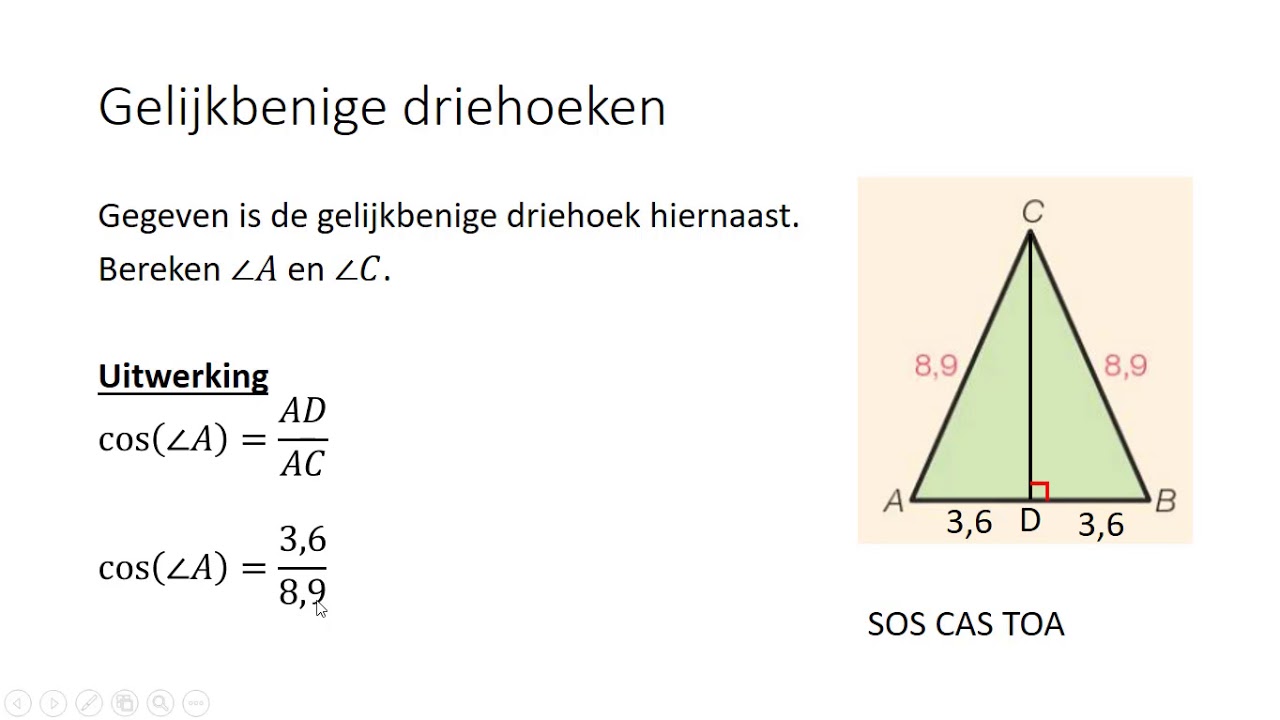
Heb je ooit naar een steile helling gekeken en je afgevraagd hoe lang die eigenlijk is? Of misschien een dakconstructie bewonderd en je gerealiseerd dat die perfecte schuine lijn cruciaal is voor de stabiliteit? De kans is groot dat de schuine zijde van een driehoek, of de hypotenusa, een rol speelt in het antwoord.

Veel mensen denken bij wiskunde aan abstracte formules en schoolboeken, maar de realiteit is dat wiskundige principes, zoals het berekenen van de schuine zijde, overal om ons heen zijn. Of je nu een doe-het-zelver bent, een architect, een ingenieur, of gewoon iemand die nieuwsgierig is naar de wereld, het begrijpen van deze berekening kan verrassend nuttig zijn. Het is niet alleen theorie; het is een praktische vaardigheid die je in staat stelt om problemen op te lossen en beter te begrijpen hoe de wereld in elkaar zit.

Waarom is de schuine zijde berekenen belangrijk?

De schuine zijde, oftewel de hypotenusa, is de langste zijde van een rechthoekige driehoek. Het is de zijde die tegenover de rechte hoek (90 graden) ligt. Het berekenen van de lengte van deze zijde is cruciaal in tal van situaties:

Constructie en Architectuur: Bij het ontwerpen van daken, bruggen, trappen en andere constructies is het essentieel om de juiste lengtes en hoeken te bepalen. De schuine zijde speelt hier een cruciale rol in het garanderen van de stabiliteit en veiligheid van de constructie.
Navigatie en Landmeetkunde: Het bepalen van afstanden over oneffen terrein, het uitzetten van koersen en het in kaart brengen van landschappen vereisen vaak de berekening van de schuine zijde.
Engineering: Van het ontwerpen van mechanische onderdelen tot het analyseren van krachten in constructies, ingenieurs maken constant gebruik van de principes van de rechthoekige driehoek en de bijbehorende berekeningen.
Doe-het-zelf Projecten: Zelfs bij simpele klusjes in huis, zoals het ophangen van een plank in een schuine hoek of het bouwen van een simpele constructie, kan het berekenen van de schuine zijde van pas komen.

De Stelling van Pythagoras: De Sleutel tot de Schuine Zijde

De Stelling van Pythagoras is de hoeksteen voor het berekenen van de schuine zijde. Deze stelling stelt dat in een rechthoekige driehoek het kwadraat van de lengte van de schuine zijde (c) gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden (a en b). Met andere woorden:

a² + b² = c²

Laten we dit eens verduidelijken met een eenvoudig voorbeeld. Stel je voor dat je een rechthoekige driehoek hebt waarbij de ene zijde (a) 3 cm lang is en de andere zijde (b) 4 cm lang is. Om de schuine zijde (c) te berekenen, volgen we de volgende stappen:

Kwadrateer de lengtes van de bekende zijden:
- a² = 3² = 9
- b² = 4² = 16
Tel de kwadraten bij elkaar op:
- a² + b² = 9 + 16 = 25
Neem de wortel van de som:
- c = √25 = 5

Dus de lengte van de schuine zijde (c) is 5 cm.

Waarom werkt dit? Een Visuele Uitleg

De Stelling van Pythagoras kan visueel worden begrepen door vierkanten te construeren op elk van de zijden van de rechthoekige driehoek. De oppervlakte van het vierkant op de schuine zijde is gelijk aan de som van de oppervlaktes van de vierkanten op de andere twee zijden. Er zijn talloze visuele bewijzen van deze stelling, waardoor het een van de meest intuïtieve en krachtige wiskundige concepten is.

Alternatieve Methoden: Trigonometrie

Hoewel de Stelling van Pythagoras perfect is wanneer je de lengtes van de twee rechthoekszijden kent, zijn er situaties waarin je een andere aanpak nodig hebt. Stel dat je de lengte van één rechthoekszijde en de hoek tussen die zijde en de schuine zijde kent. In dat geval komt trigonometrie om de hoek kijken.

Trigonometrie is de tak van de wiskunde die zich bezighoudt met de relaties tussen de hoeken en de zijden van driehoeken. De belangrijkste trigonometrische functies zijn sinus (sin), cosinus (cos) en tangens (tan).

Om de schuine zijde te berekenen met behulp van trigonometrie, kunnen we de volgende formules gebruiken:

Als je de aanliggende zijde (a) en de hoek (α) tussen de aanliggende zijde en de schuine zijde kent:
- c = a / cos(α)
Als je de overstaande zijde (b) en de hoek (α) tussen de schuine zijde en de aanliggende zijde kent:
- c = b / sin(α)

Voorbeeld: Stel dat je een rechthoekige driehoek hebt waarbij de aanliggende zijde (a) 8 cm lang is en de hoek (α) tussen de aanliggende zijde en de schuine zijde 30 graden is. Om de schuine zijde (c) te berekenen, gebruiken we de volgende formule:

c = 8 / cos(30°) ≈ 8 / 0.866 ≈ 9.24 cm

Dus de lengte van de schuine zijde (c) is ongeveer 9.24 cm.

Wanneer Trigonometrie gebruiken?

Trigonometrie is handig wanneer je niet de lengtes van beide rechthoekszijden kent, maar wel de lengte van één rechthoekszijde en een hoek. Het is ook essentieel in situaties waarin je geen rechthoekige driehoek hebt, maar wel andere hoeken en zijden kent. In die gevallen kun je de sinusregel of cosinusregel gebruiken om de ontbrekende zijden en hoeken te berekenen.

Mogelijke Verwarringen en Valkuilen

Hoewel de Stelling van Pythagoras en trigonometrie relatief eenvoudig zijn, zijn er enkele veelvoorkomende fouten die mensen maken:

Vergeten te kwadrateren: Een veelgemaakte fout is het vergeten om de lengtes van de zijden te kwadrateren voordat ze bij elkaar worden opgeteld. Zorg er altijd voor dat je a² en b² berekent, niet alleen a en b.
Verkeerde zijden gebruiken: Zorg ervoor dat je de juiste zijden identificeert als de aanliggende, overstaande en schuine zijde, vooral bij het gebruik van trigonometrie. Een verkeerde identificatie kan leiden tot een verkeerd resultaat.
Vergeten de wortel te trekken: Nadat je a² + b² hebt berekend, moet je de wortel trekken om de lengte van de schuine zijde (c) te vinden. Vergeet deze laatste stap niet!
Rekenmachine-instellingen: Bij het gebruik van trigonometrische functies is het belangrijk om te controleren of je rekenmachine in de juiste modus staat (graden of radialen). Een verkeerde instelling kan leiden tot een verkeerd resultaat.

Sommige mensen beweren dat je deze formules nooit in het echte leven nodig zult hebben, omdat je alles kunt meten. Hoewel dit tot op zekere hoogte waar is, is het belangrijk te onthouden dat metingen niet altijd mogelijk of nauwkeurig zijn. Soms is het berekenen van de schuine zijde de enige manier om een nauwkeurig resultaat te krijgen, vooral bij complexe of moeilijk toegankelijke constructies.

Tools en Hulpmiddelen

Gelukkig zijn er tegenwoordig tal van tools en hulpmiddelen beschikbaar om het berekenen van de schuine zijde te vereenvoudigen:

Online Calculators: Er zijn talloze online calculators beschikbaar die je kunt gebruiken om de schuine zijde te berekenen. Je hoeft alleen de lengtes van de bekende zijden in te vullen en de calculator doet de rest.
Rekenmachines: Moderne rekenmachines hebben vaak trigonometrische functies ingebouwd, waardoor het gemakkelijk is om de schuine zijde te berekenen met behulp van de formules die we hebben besproken.
Smartphone Apps: Er zijn diverse smartphone apps beschikbaar die speciaal zijn ontworpen voor wiskundige berekeningen, waaronder het berekenen van de schuine zijde.
Geometrie Software: Voor meer complexe berekeningen en visualisaties kun je gebruik maken van geometrie software zoals GeoGebra of SketchUp.

Deze tools kunnen je helpen om tijd te besparen en fouten te voorkomen. Het is echter belangrijk om de basisprincipes van de Stelling van Pythagoras en trigonometrie te begrijpen, zodat je de resultaten kunt interpreteren en controleren.

Een Oproep tot Actie

Het berekenen van de schuine zijde is meer dan alleen een wiskundige oefening; het is een vaardigheid die je in staat stelt om de wereld om je heen beter te begrijpen en problemen op te lossen. Of je nu een student bent, een professional of gewoon iemand die nieuwsgierig is, ik hoop dat dit artikel je heeft geïnspireerd om je wiskundige kennis verder te ontwikkelen.

Dus, waar wacht je nog op? Ga op zoek naar rechthoekige driehoeken in je omgeving en oefen met het berekenen van de schuine zijde. Gebruik de tools en hulpmiddelen die we hebben besproken en daag jezelf uit met steeds complexere problemen.

Welke projecten of situaties zie jij voor je waarin je de kennis over de schuine zijde in de toekomst zou kunnen gebruiken?