Stelling Van Pythagoras Hoeken Berekenen

Heb je je ooit afgevraagd hoe landmeters de hoogte van een berg bepalen zonder daadwerkelijk naar de top te klimmen? Of hoe timmerlieden controleren of een hoek perfect recht is? Het antwoord ligt in een eeuwenoude wiskundige formule: de stelling van Pythagoras. Dit artikel is speciaal geschreven voor leerlingen in het voortgezet onderwijs, hobbyisten en iedereen die zijn wiskundige vaardigheden wil opfrissen. We gaan dieper in op de stelling van Pythagoras en hoe je deze kunt gebruiken om zowel zijden als hoeken van rechthoekige driehoeken te berekenen. Maak je klaar voor een praktische en begrijpelijke uitleg!

Wat is de Stelling van Pythagoras?

De stelling van Pythagoras is een fundamenteel concept in de meetkunde, met name in de studie van rechthoekige driehoeken. Een rechthoekige driehoek is een driehoek met één hoek van precies 90 graden (een rechte hoek). De stelling beschrijft de relatie tussen de lengtes van de zijden van deze driehoek.

Laten we de zijden van de rechthoekige driehoek benoemen:

• De twee korte zijden, die de rechte hoek vormen, noemen we de rechthoekszijden (a en b).
• De langste zijde, die tegenover de rechte hoek ligt, noemen we de hypotenusa (c).

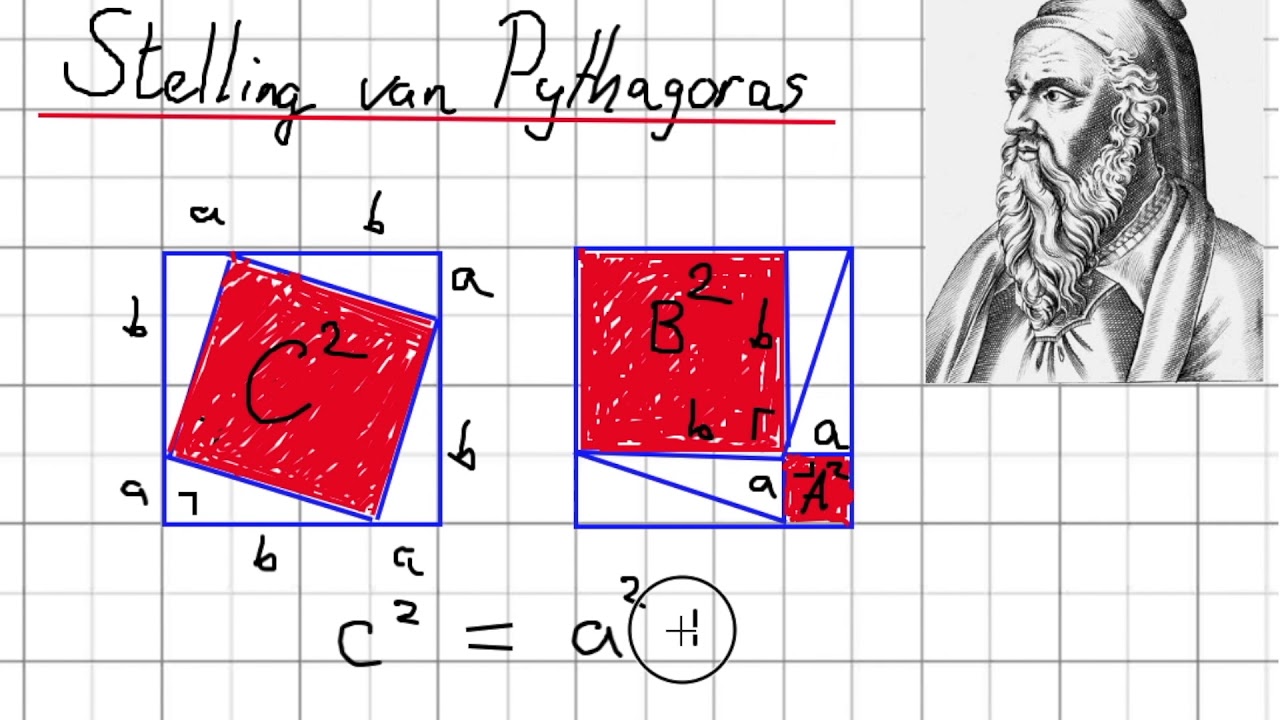
De stelling van Pythagoras stelt nu het volgende:

a² + b² = c²

In woorden: het kwadraat van de ene rechthoekszijde, plus het kwadraat van de andere rechthoekszijde, is gelijk aan het kwadraat van de hypotenusa.

Een Praktisch Voorbeeld

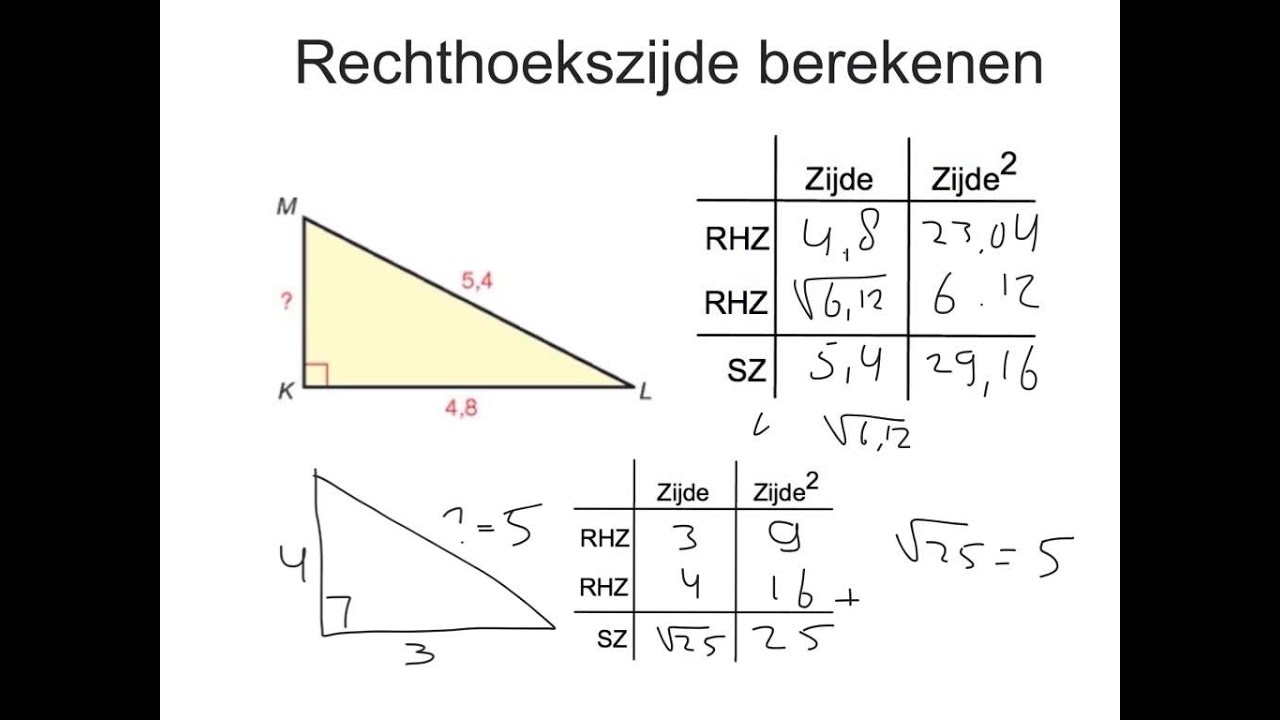
Stel, we hebben een rechthoekige driehoek waarbij de ene rechthoekszijde 3 cm lang is (a = 3) en de andere rechthoekszijde 4 cm lang is (b = 4). Hoe lang is de hypotenusa (c)?

We passen de stelling van Pythagoras toe:

3² + 4² = c²

9 + 16 = c²

25 = c²

Om c te vinden, nemen we de wortel van 25:

c = √25 = 5

Dus de hypotenusa is 5 cm lang.

Hoe Bereken je Zijden met de Stelling van Pythagoras?

De stelling van Pythagoras kan worden gebruikt om de lengte van elke zijde van een rechthoekige driehoek te berekenen, zolang je de lengte van de andere twee zijden kent. Laten we de verschillende scenario's bekijken:

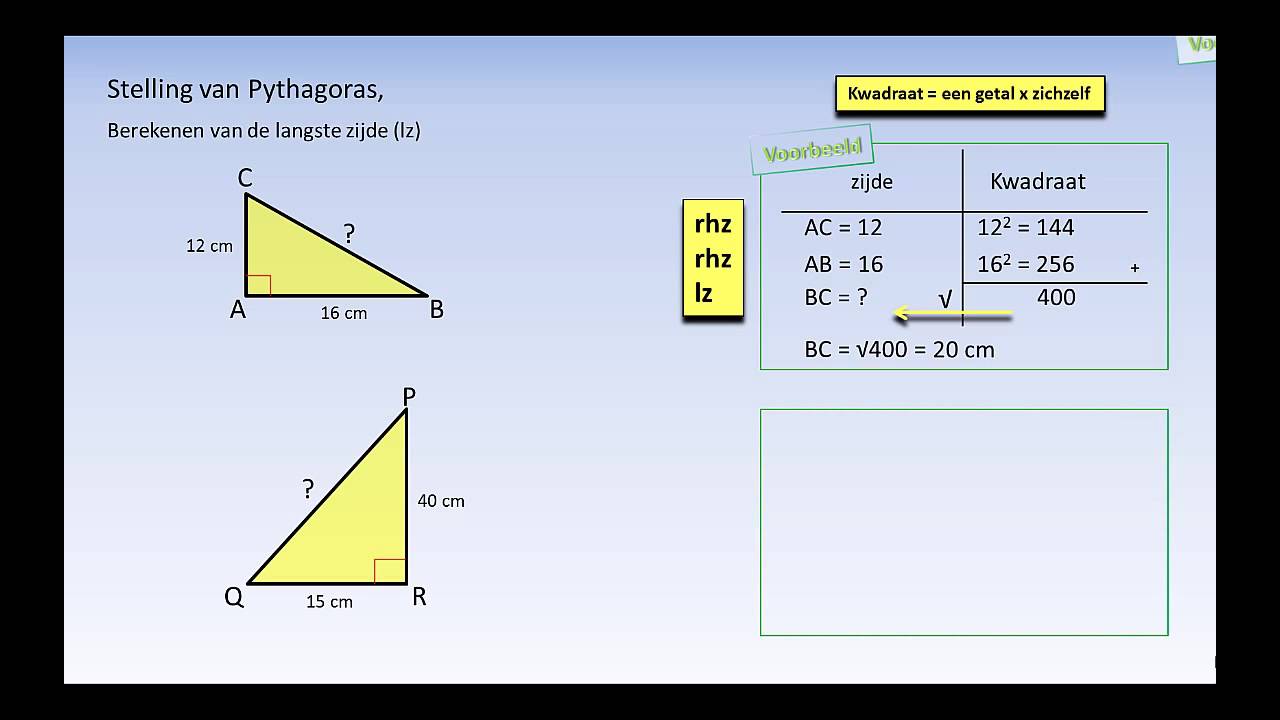
1. Hypotenusa Berekenen (c)

Zoals we in het vorige voorbeeld hebben gezien, is de formule om de hypotenusa te berekenen:

c = √(a² + b²)

2. Rechthoekszijde Berekenen (a of b)

Stel dat je de hypotenusa (c) en één van de rechthoekszijden (bijvoorbeeld b) kent, en je wilt de andere rechthoekszijde (a) berekenen. Dan kun je de formule herschrijven:

a² = c² - b²

a = √(c² - b²)

Hetzelfde geldt als je b wilt berekenen:

b² = c² - a²

b = √(c² - a²)

Een Ander Voorbeeld

Een ladder van 6 meter lang staat tegen een muur. De voet van de ladder staat 2 meter van de muur af. Hoe hoog reikt de ladder op de muur?

In dit geval is de ladder de hypotenusa (c = 6 meter), de afstand van de muur tot de voet van de ladder is een rechthoekszijde (b = 2 meter), en de hoogte die we willen weten is de andere rechthoekszijde (a).

We gebruiken de formule:

a = √(c² - b²)

a = √(6² - 2²)

a = √(36 - 4)

a = √32

a ≈ 5.66 meter

De ladder reikt dus ongeveer 5.66 meter hoog op de muur.

Hoeken Berekenen in een Rechthoekige Driehoek

Naast het berekenen van de zijden, kun je de stelling van Pythagoras (indirect) gebruiken om hoeken in een rechthoekige driehoek te berekenen, samen met trigonometrische functies. Trigonometrie is de tak van de wiskunde die zich bezighoudt met de relaties tussen de zijden en hoeken van driehoeken.

De belangrijkste trigonometrische functies zijn:

• Sinus (sin): sin(hoek) = Overstaande zijde / Hypotenusa
• Cosinus (cos): cos(hoek) = Aanliggende zijde / Hypotenusa
• Tangens (tan): tan(hoek) = Overstaande zijde / Aanliggende zijde

In een rechthoekige driehoek, als je de lengtes van twee zijden kent, kun je de hoeken berekenen met behulp van de inverse trigonometrische functies (arcsin, arccos, arctan), ook wel aangeduid als sin^-1, cos^-1, en tan^-1.

Voorbeeld: Hoek Berekenen met Tangens

Stel, in een rechthoekige driehoek is de overstaande zijde 5 cm en de aanliggende zijde 7 cm. We willen de hoek (θ) berekenen tussen de aanliggende zijde en de hypotenusa.

We weten dat:

tan(θ) = Overstaande zijde / Aanliggende zijde

tan(θ) = 5 / 7

Om θ te vinden, gebruiken we de inverse tangens (arctan of tan^-1):

θ = tan^-1(5/7)

θ ≈ 35.54 graden

De hoek is dus ongeveer 35.54 graden.

Wanneer Gebruik je Welke Trigonometrische Functie?

Het hangt af van welke zijden je kent:

• Overstaande en Hypotenusa bekend: Gebruik de sinus (sin^-1).
• Aanliggende en Hypotenusa bekend: Gebruik de cosinus (cos^-1).
• Overstaande en Aanliggende bekend: Gebruik de tangens (tan^-1).

Belangrijke Aandachtspunten

• Rechte Hoek: De stelling van Pythagoras geldt alleen voor rechthoekige driehoeken.
• Eenheden: Zorg ervoor dat alle zijden in dezelfde eenheid zijn (bijvoorbeeld allemaal in centimeters of meters).
• Rekenmachine: Voor het berekenen van inverse trigonometrische functies heb je een rekenmachine nodig met sin^-1, cos^-1 en tan^-1 functies.
• Afronden: Rond je antwoorden pas af aan het einde van de berekening om nauwkeurigheid te behouden.

Toepassingen in het Dagelijks Leven

De stelling van Pythagoras is niet alleen een theoretisch concept; het heeft talloze praktische toepassingen:

• Bouwkunde: Gebruikt voor het uitzetten van rechte hoeken, het berekenen van dakhellingen, en het controleren van de stabiliteit van constructies.
• Navigatie: Gebruikt om afstanden en posities te bepalen, bijvoorbeeld in de scheepvaart en luchtvaart.
• Landmeetkunde: Gebruikt voor het bepalen van de hoogte van bergen, de afstand tussen punten, en het uitzetten van landgrenzen.
• Timmerwerk: Gebruikt om ervoor te zorgen dat hoeken recht zijn bij het bouwen van meubels, ramen en deuren.
• Computergraphics: Gebruikt voor het berekenen van afstanden en perspectieven in 3D-modellen en games.

Oefenen Baart Kunst!

De beste manier om de stelling van Pythagoras en het berekenen van hoeken onder de knie te krijgen, is door te oefenen. Zoek online naar oefenopgaven, of maak je eigen voorbeelden. Experimenteer met verschillende waarden en probeer de formules toe te passen in verschillende situaties. Vraag je docent of medeleerlingen om hulp als je vastloopt.

Onthoud dat de stelling van Pythagoras een krachtig hulpmiddel is dat je kunt gebruiken om problemen in de wiskunde, wetenschap en het dagelijks leven op te lossen. Blijf oefenen, en je zult versteld staan van wat je kunt bereiken!

Conclusie

De stelling van Pythagoras is een essentieel concept in de wiskunde dat ons in staat stelt om zijden en (indirect) hoeken in rechthoekige driehoeken te berekenen. Door de formule a² + b² = c² te begrijpen en toe te passen, kun je een breed scala aan praktische problemen oplossen, van het bouwen van een huis tot het navigeren op zee. Met de toevoeging van trigonometrische functies, kun je nauwkeurig hoeken berekenen en de relaties tussen zijden en hoeken volledig begrijpen. We hopen dat dit artikel je heeft geholpen om een beter begrip te krijgen van dit belangrijke wiskundige principe. Ga nu aan de slag en ontdek de kracht van Pythagoras zelf!