Tangens Van Een Hoek Berekenen
Heb je ooit voor een wiskundeopgave gezeten waarbij je de tangens van een hoek moest berekenen en je je afvroeg: "Waar begin ik in vredesnaam?". Je bent zeker niet de enige! Trigonometrie kan soms als een doolhof aanvoelen, maar met de juiste uitleg en een beetje oefening wordt het een stuk helderder. Dit artikel is er om je stap voor stap te begeleiden bij het berekenen van de tangens, zodat je die opgaven met vertrouwen kunt aanpakken.
Wat is de Tangens eigenlijk?
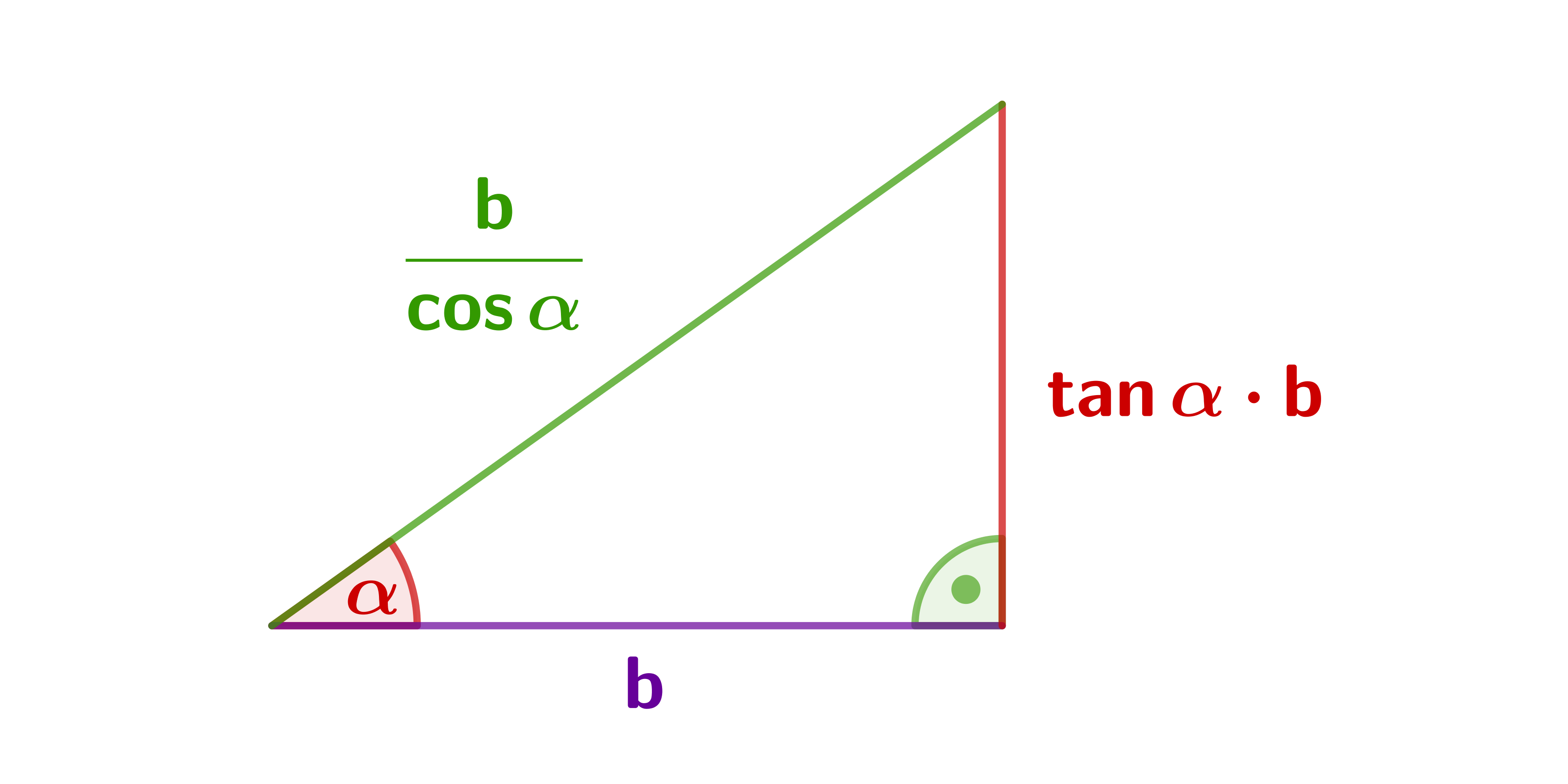
Laten we beginnen met de basis. De tangens (vaak afgekort tot tan) is een trigonometrische functie die de verhouding beschrijft tussen de overstaande zijde en de aanliggende zijde van een rechthoekige driehoek ten opzichte van een bepaalde hoek. Stel je een rechthoekige driehoek voor. De langste zijde, tegenover de rechte hoek (90 graden), noemen we de hypotenusa. De andere twee zijden zijn de overstaande en aanliggende zijde, afhankelijk van welke hoek we bekijken (anders dan de rechte hoek zelf).
Dus, de formule voor de tangens is:
tan(hoek) = Overstaande zijde / Aanliggende zijde
Denk er aan: SOH CAH TOA! Dit ezelsbruggetje helpt je de basis trigonometrische functies te onthouden. TOA staat voor Tangens = Overstaande / Aanliggende.
Waarom is de Tangens Belangrijk?
De tangens is veel meer dan alleen een wiskundige formule. Het wordt gebruikt in talloze praktische toepassingen, zoals:
- Navigatie: Om hoeken en afstanden te bepalen bij het varen of vliegen.
- Bouwkunde: Om hellingshoeken van daken of bruggen te berekenen.
- Landmeetkunde: Om de hoogte van bergen of de diepte van valleien te meten.
- Natuurkunde: Om bewegingen en krachten te analyseren.
- Game development: Om realistische bewegingen en perspectieven in games te creëren.
Zonder de tangens zouden veel van deze toepassingen veel moeilijker, zo niet onmogelijk, zijn. Het is een fundamenteel concept dat de basis vormt voor veel wetenschappelijke en technische disciplines.
De Tangens Berekenen: Stap voor Stap
Nu we weten wat de tangens is en waarom het belangrijk is, gaan we kijken hoe je het kunt berekenen. Hier zijn de stappen:
Stap 1: Identificeer de Rechthoekige Driehoek
Zorg ervoor dat je een rechthoekige driehoek hebt. Een rechthoekige driehoek heeft per definitie één hoek van 90 graden. Dit is cruciaal, want de tangens functie is alleen gedefinieerd voor rechthoekige driehoeken.
Stap 2: Bepaal de Hoek
Bepaal de specifieke hoek waarvoor je de tangens wilt berekenen. Het gaat om een van de hoeken die niet de rechte hoek is.
Stap 3: Identificeer de Overstaande en Aanliggende Zijde
Identificeer de overstaande en aanliggende zijde ten opzichte van de gekozen hoek. De overstaande zijde is de zijde die tegenover de hoek ligt. De aanliggende zijde is de zijde die naast de hoek ligt (en geen hypotenusa is).
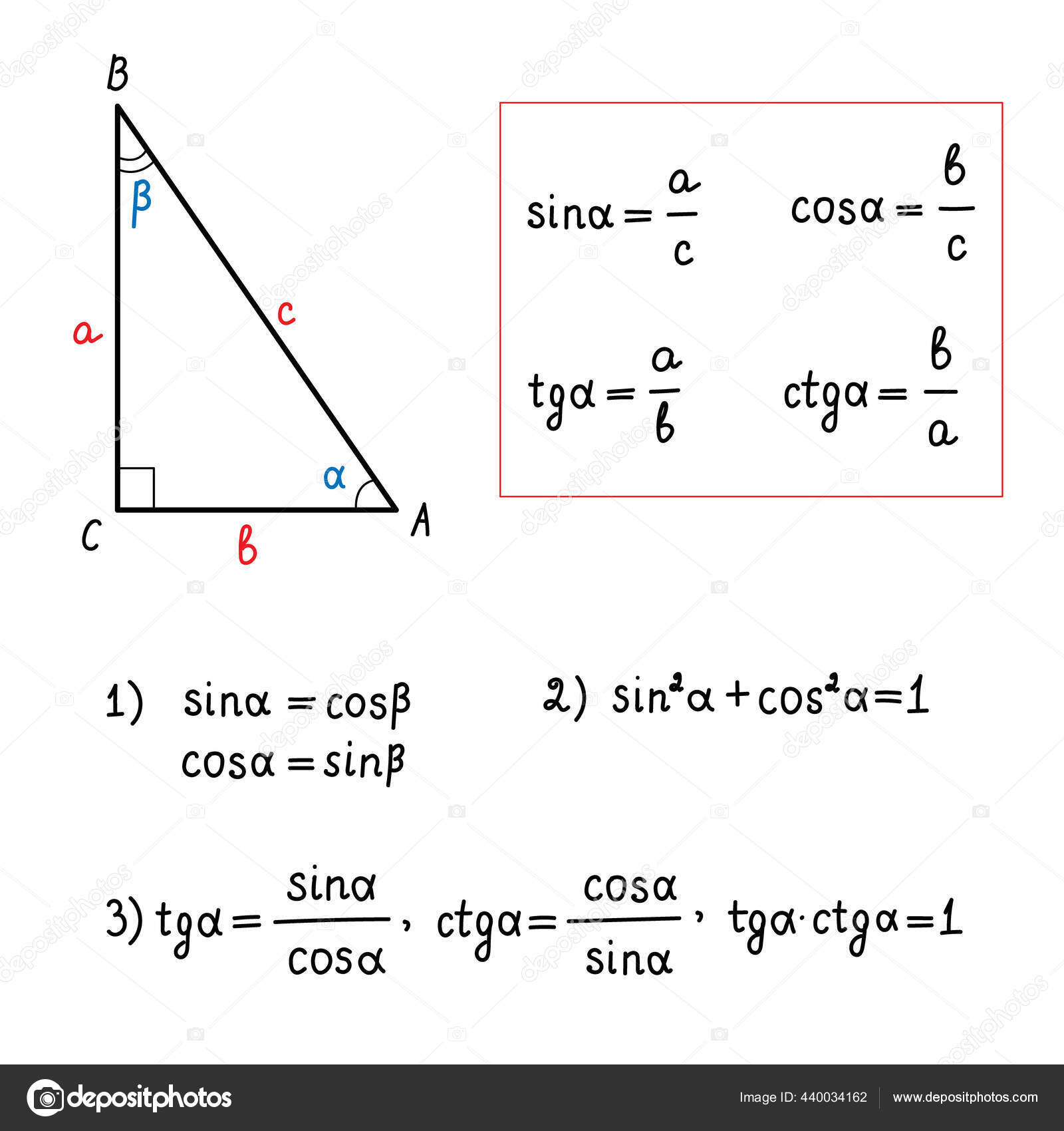
Voorbeeld: Stel, je hebt een rechthoekige driehoek ABC, waarbij hoek C 90 graden is. Je wilt de tangens van hoek A berekenen. De overstaande zijde van hoek A is BC, en de aanliggende zijde is AC.
Stap 4: Meet de Lengte van de Zijden
Meet de lengte van de overstaande en aanliggende zijde. Zorg ervoor dat je dezelfde meeteenheid gebruikt voor beide zijden (bijvoorbeeld centimeters, meters, inches, etc.). Nauwkeurigheid is hier belangrijk, want een kleine fout in de meting kan een groot verschil maken in het resultaat.
Stap 5: Pas de Formule toe
Deel de lengte van de overstaande zijde door de lengte van de aanliggende zijde. Dit geeft je de waarde van de tangens van de hoek:
tan(A) = Lengte van overstaande zijde / Lengte van aanliggende zijde
Voorbeeld (vervolg): Stel, de lengte van BC (overstaande zijde) is 5 cm en de lengte van AC (aanliggende zijde) is 12 cm. Dan is:
tan(A) = 5 cm / 12 cm = 0.4167
De tangens van hoek A is dus 0.4167.
Tangens Berekenen met een Rekenmachine
In veel gevallen, vooral bij complexe hoeken, is het handiger om een rekenmachine te gebruiken. Moderne rekenmachines hebben een tan-knop die direct de tangens van een hoek kan berekenen. Let wel op de instelling van je rekenmachine (graden of radialen!).
Stappen:
- Zorg ervoor dat je rekenmachine in de juiste modus staat (graden of radialen). Dit is cruciaal! Als je een hoek in graden hebt, moet de rekenmachine in "DEG" modus staan. Als je een hoek in radialen hebt, moet de rekenmachine in "RAD" modus staan.
- Voer de hoek in.
- Druk op de tan-knop.
- Het resultaat is de tangens van de hoek.
Voorbeeld: Je wilt de tangens van 45 graden berekenen. Zorg ervoor dat je rekenmachine in "DEG" modus staat. Voer "45" in en druk op de tan-knop. Het resultaat is 1. Dit komt omdat in een rechthoekige driehoek met een hoek van 45 graden, de overstaande en aanliggende zijde gelijk zijn in lengte, en dus de deling 1 oplevert.
Veelgemaakte Fouten en Hoe ze te Vermijden
Hier zijn enkele veelgemaakte fouten bij het berekenen van de tangens en hoe je ze kunt vermijden:
- Verkeerde modus op de rekenmachine: Controleer altijd of je rekenmachine in de juiste modus (graden of radialen) staat. Dit is een veelvoorkomende fout die tot compleet verkeerde resultaten leidt.
- Overstaande en aanliggende zijde verwisselen: Zorg ervoor dat je de overstaande en aanliggende zijde correct identificeert ten opzichte van de gekozen hoek.
- Verkeerde driehoek: De tangens functie is alleen gedefinieerd voor rechthoekige driehoeken. Zorg ervoor dat je een rechthoekige driehoek hebt voordat je de tangens probeert te berekenen.
- Meetfouten: Wees nauwkeurig bij het meten van de lengte van de zijden. Kleine meetfouten kunnen een aanzienlijke invloed hebben op het resultaat.
Oefenen Baart Kunst
De beste manier om de tangens te leren berekenen is door te oefenen. Probeer verschillende voorbeelden met verschillende hoeken en zijdelengtes. Gebruik een rekenmachine om je antwoorden te controleren. Je kunt online ook veel oefeningen vinden. Zoek bijvoorbeeld naar "trigonometrie oefeningen" of "tangens berekenen oefeningen".
Begin met eenvoudige voorbeelden en werk geleidelijk aan naar complexere problemen. Hoe meer je oefent, hoe beter je het concept zult begrijpen en hoe zelfverzekerder je zult worden in het berekenen van de tangens.
Conclusie
De tangens is een belangrijke trigonometrische functie met talloze praktische toepassingen. Door de stappen in dit artikel te volgen en te oefenen, kun je de tangens met vertrouwen berekenen en de principes van trigonometrie beter begrijpen. Onthoud SOH CAH TOA, controleer de modus van je rekenmachine, en oefen, oefen, oefen! Succes met je wiskunde avonturen!
Bekijk ook deze gerelateerde berichten:
- Hoeveel Bladzijden Per Uur Lezen Hbo
- Hoe Kan Ik Een Cv Maken
- Onze Vader Die In De Hemel Zijt Katholiek
- Wat Zie Je Op Een Rontgenfoto
- Krapte Op De Arbeidsmarkt Betekenis
- Hoe Bereken Je Een Deel Van Het Geheel
- Welke Straf Voor Welk Misdrijf
- 60 Gram Ongekookte Rijst Is Hoeveel Gekookt
- Over Hoeveel Weken Is Het Zomervakantie 2024
- Hoelang Voordat Nicotine Uit Je Lichaam Is
