Uitleg Wiskunde Getal En Ruimte Havo/vwo 2

Ben je net begonnen met Getal en Ruimte in de 2e klas havo/vwo? Of vind je het gewoon lastig om bepaalde onderwerpen te begrijpen? Je bent niet de enige! Veel leerlingen worstelen met wiskunde, en Getal en Ruimte kan soms best pittig zijn. In dit artikel help ik je de belangrijkste onderwerpen te begrijpen en geef ik je tips om je wiskundige vaardigheden te verbeteren. We snappen dat wiskunde soms aanvoelt als een abstracte puzzel, maar we gaan laten zien hoe relevant het eigenlijk is.

Waarom Wiskunde Belangrijk Is (En Waarom Je Niet Moet Opgeven!)

Voordat we de specifieke onderwerpen induiken, is het belangrijk om te begrijpen waarom wiskunde belangrijk is. Het gaat niet alleen om het halen van een goed cijfer. Wiskunde traint je logisch denken, je probleemoplossende vaardigheden en je analytisch vermogen. Deze vaardigheden zijn nuttig in heel veel verschillende situaties, zowel op school als in het dagelijks leven.

Denk bijvoorbeeld aan:

Budgetteren: Bepalen hoeveel geld je kunt uitgeven en hoe je je spaargeld kunt beheren.
Recepten aanpassen: Weten hoe je de hoeveelheden ingrediënten moet aanpassen als je voor meer of minder mensen kookt.
Kortingen berekenen: Snel uitrekenen welke aanbieding de beste deal is.
Kaartlezen en navigeren: Afstanden inschatten en de kortste route bepalen.

Ook in veel beroepen is wiskunde onmisbaar. Denk aan ingenieurs, programmeurs, economen en data-analisten. Zelfs als je geen bèta-beroep ambieert, zul je merken dat je wiskundige vaardigheden van pas komen.

Natuurlijk, je kunt zeggen: "Ik ga toch geen ingenieur worden, dus waarom zou ik me druk maken?" Dat is een geldig punt! Maar de vaardigheden die je opdoet tijdens het leren van wiskunde, zijn transfereerbaar. Ze helpen je om kritisch te denken, problemen op te lossen en informatie te analyseren. En dat is iets waar je de rest van je leven profijt van zult hebben.

Belangrijke Onderwerpen in Getal en Ruimte Havo/vwo 2

In de tweede klas van havo/vwo komen er vaak verschillende wiskundige onderwerpen aan bod. We zullen enkele belangrijke onderwerpen bespreken en tips geven om ze beter te begrijpen.

1. Rekenen met Breuken, Decimale Getallen en Procenten

Dit is een fundamenteel onderdeel van de wiskunde. Het is belangrijk dat je snel en accuraat kunt rekenen met breuken, decimale getallen en procenten. Veel andere wiskundige onderwerpen bouwen hierop voort.

Breuken: Vereenvoudigen, gelijknamig maken, optellen, aftrekken, vermenigvuldigen en delen.
Decimale getallen: Omzetten van breuken naar decimale getallen en omgekeerd. Optellen, aftrekken, vermenigvuldigen en delen.
Procenten: Berekenen van een percentage van een getal, een percentage verhogen of verlagen, en het percentage berekenen van een verandering.

Tip: Oefen regelmatig met sommen. Gebruik online oefenmateriaal of maak extra opgaven uit je boek. Zorg ervoor dat je de basisprincipes goed begrijpt voordat je verdergaat.

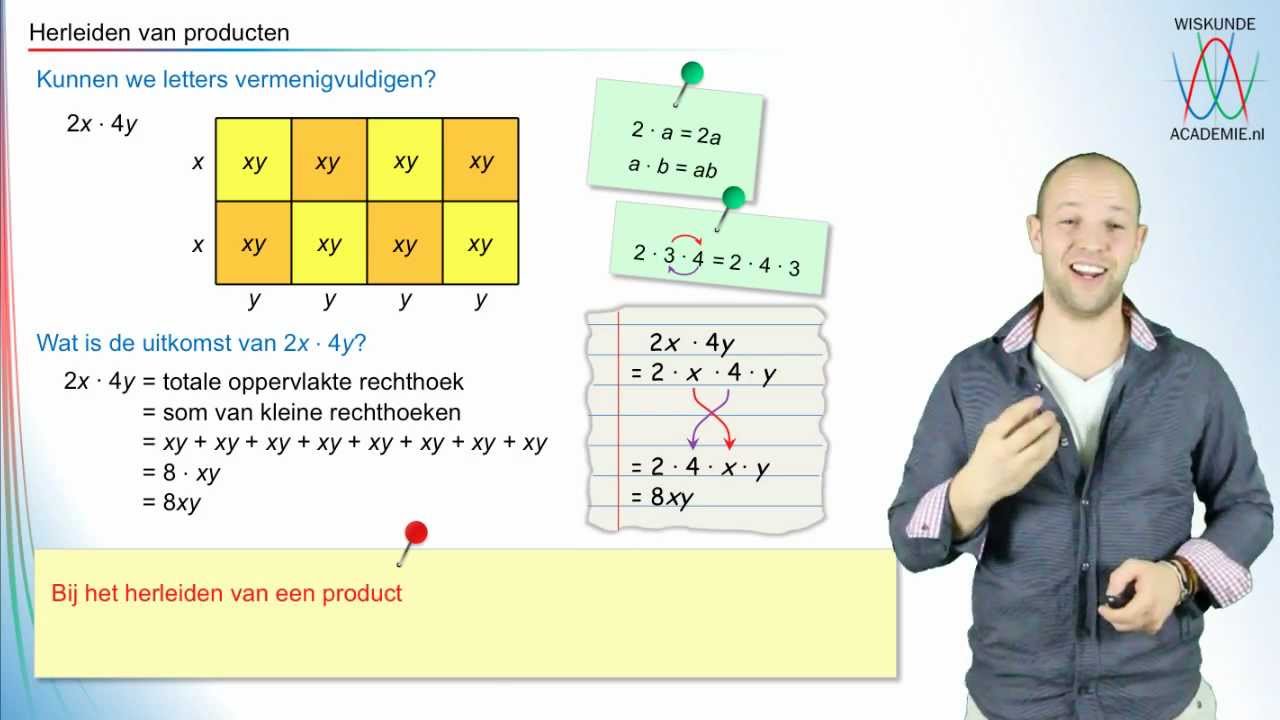
2. Algebraïsche Vaardigheden: Vergelijkingen en Ongelijkheden

Algebra is het deel van de wiskunde dat zich bezighoudt met letters en symbolen. Je leert vergelijkingen oplossen, formules herschrijven en ongelijkheden oplossen.

Vergelijkingen: Lineaire vergelijkingen oplossen, kwadratische vergelijkingen oplossen (eventueel met de abc-formule).
Formules: Formules herschrijven om een bepaalde variabele uit te drukken in andere variabelen.
Ongelijkheden: Lineaire ongelijkheden oplossen en de oplossing weergeven op een getallenlijn.

Tip: Wees nauwkeurig bij het opschrijven van je berekeningen. Maak geen slordige fouten. Controleer je antwoorden altijd door ze in de oorspronkelijke vergelijking of ongelijkheid in te vullen.

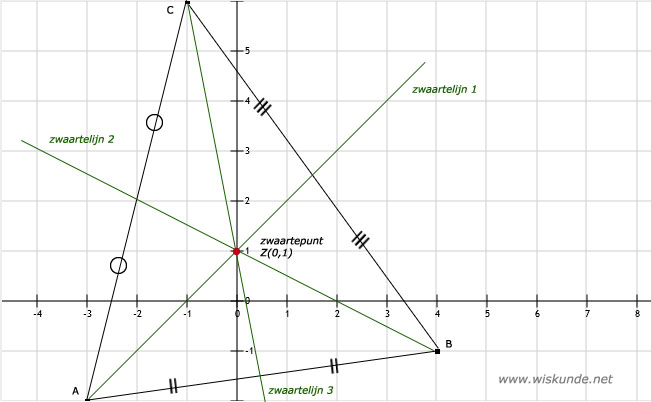
3. Meetkunde: Vormen, Hoeken en Oppervlakte

Meetkunde gaat over vormen, afmetingen en ruimtelijke figuren. Je leert over hoeken, lijnen, driehoeken, vierhoeken, cirkels en andere meetkundige figuren. Ook het berekenen van oppervlakte en inhoud komt aan bod.

Hoeken: Meten en berekenen van hoeken, zoals rechte hoeken, scherpe hoeken en stompe hoeken.
Driehoeken: Soorten driehoeken (gelijkzijdig, gelijkbenig, rechthoekig), hoeken en zijden berekenen.
Vierhoeken: Soorten vierhoeken (vierkant, rechthoek, parallellogram, ruit, trapezium), hoeken en zijden berekenen.
Cirkels: Berekenen van de omtrek en oppervlakte van een cirkel.
Oppervlakte en inhoud: Berekenen van de oppervlakte van verschillende figuren en de inhoud van verschillende ruimtelijke figuren.

Tip: Maak gebruik van tekeningen en schema's om de meetkundige figuren beter te visualiseren. Leer de belangrijke formules uit je hoofd. Oefen met het berekenen van oppervlaktes en inhouden van verschillende objecten in je omgeving.

4. Functies en Grafieken

Een functie beschrijft een relatie tussen twee variabelen. Je leert over lineaire functies, kwadratische functies en andere soorten functies. Je leert ook hoe je grafieken van functies kunt tekenen en interpreteren.

Lineaire functies: De vorm y = ax + b. Herkennen van de richtingscoëfficiënt (a) en het begingetal (b).
Kwadratische functies: De vorm y = ax² + bx + c. Bepalen van de top en de nulpunten.
Grafieken tekenen: Punten uitzetten en een vloeiende lijn trekken.
Grafieken interpreteren: Aflezen van waarden, bepalen van stijging en daling, vinden van maxima en minima.

Tip: Gebruik een grafische rekenmachine of online grafiekentool om de grafieken van functies te visualiseren. Oefen met het interpreteren van grafieken en het aflezen van waarden.

Hoe Los Je Problemen op? Een Stappenplan

Wiskunde is niet altijd makkelijk. Soms kom je vast te zitten en weet je niet hoe je verder moet. Hier is een stappenplan dat je kunt gebruiken om problemen op te lossen:

Lees de opgave aandachtig: Zorg ervoor dat je begrijpt wat er gevraagd wordt. Markeer de belangrijke informatie.
Maak een schets of tekening: Dit kan je helpen om de situatie beter te visualiseren.
Schrijf de bekende gegevens op: Noteer alle informatie die je hebt gekregen.
Zoek de juiste formule of regel: Bepaal welke wiskundige principes van toepassing zijn.
Vul de formule in: Vervang de variabelen door de bekende waarden.
Los de vergelijking op: Voer de berekeningen uit.
Controleer je antwoord: Klopt je antwoord? Is het logisch?

Onthoud: Fouten maken is normaal. Van fouten leer je. Probeer niet te snel op te geven. Blijf proberen en vragen stellen!

Tips voor een Betere Leerervaring

Hier zijn nog enkele algemene tips die je kunnen helpen om je wiskundige vaardigheden te verbeteren:

Wees actief in de les: Stel vragen als je iets niet begrijpt.
Maak je huiswerk op tijd: Stel het niet uit tot het laatste moment.
Oefen regelmatig: Wiskunde leer je door te doen.
Zoek hulp als je het nodig hebt: Vraag je docent, een klasgenoot of een bijlesdocent om hulp.
Gebruik online hulpmiddelen: Er zijn veel websites en apps die je kunnen helpen met wiskunde.
Maak het leuk: Probeer wiskunde te zien als een uitdaging, niet als een straf.

Conclusie

Wiskunde kan een uitdaging zijn, maar met de juiste aanpak en een beetje doorzettingsvermogen kan iedereen het leren. Onthoud dat wiskunde meer is dan alleen maar formules en berekeningen. Het is een manier van denken en een krachtig hulpmiddel om problemen op te lossen. Door je wiskundige vaardigheden te verbeteren, investeer je in je toekomst.

Wat is jouw grootste uitdaging bij wiskunde op dit moment, en wat ga je doen om die uitdaging aan te pakken?