Verhouding Berekenen Tussen 2 Getallen

Heb je ooit het gevoel gehad dat je verdwaalt in een zee van cijfers? Probeer je een recept aan te passen, een budget te beheren, of simpelweg te begrijpen of je een goede deal krijgt in de uitverkoop? Dan is de kans groot dat je worstelt met verhoudingen. Je bent niet de enige! Veel mensen vinden het lastig om verhoudingen te berekenen en te begrijpen, wat kan leiden tot frustratie en fouten. In dit artikel duiken we diep in de wereld van verhoudingen, leggen we uit hoe je ze berekent en laten we zien hoe je ze in de praktijk kunt toepassen. We pakken het stap voor stap aan, zodat het voor iedereen begrijpelijk is.

Waarom zijn verhoudingen belangrijk?

Verhoudingen zijn overal om ons heen. Ze vormen de basis voor:

• Recepten: De hoeveelheid ingrediënten moet in de juiste verhouding zijn om een smakelijk gerecht te bereiden.
• Financiën: Het begrijpen van je inkomsten en uitgaven in verhouding tot elkaar is cruciaal voor een gezonde financiële situatie.
• Winkelen: Je kunt de verhouding tussen prijs en kwaliteit vergelijken om de beste deal te vinden.
• Bouw en constructie: Verhoudingen zijn essentieel voor nauwkeurige metingen en het creëren van stabiele structuren.
• Kaarten en schaalmodellen: Ze vertegenwoordigen de werkelijkheid op een kleinere schaal, waarbij de verhoudingen behouden blijven.

Het correct berekenen van verhoudingen helpt je dus om betere beslissingen te nemen in je dagelijks leven en om problemen efficiënter op te lossen.

Wat is een verhouding eigenlijk?

Een verhouding is een manier om twee of meer hoeveelheden met elkaar te vergelijken. Het laat zien hoe de hoeveelheden zich tot elkaar verhouden. We kunnen een verhouding op verschillende manieren uitdrukken:

• Als breuk: bijvoorbeeld 1/2 (één op twee)
• Met een dubbele punt: bijvoorbeeld 1:2 (één staat tot twee)
• In woorden: bijvoorbeeld "één op de twee"

Laten we een simpel voorbeeld nemen: Stel, je hebt een fruitschaal met 3 appels en 6 bananen. De verhouding tussen appels en bananen is dan 3:6. Dit betekent dat er voor elke 3 appels, 6 bananen zijn. Deze verhouding kunnen we ook vereenvoudigen.

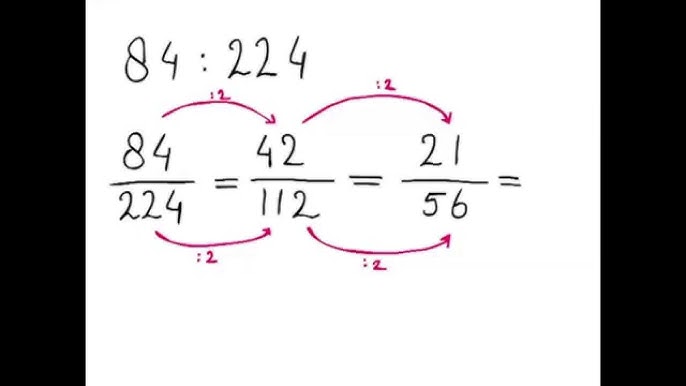
Vereenvoudigen van verhoudingen

Net als breuken kunnen verhoudingen vaak worden vereenvoudigd. Om een verhouding te vereenvoudigen, deel je alle getallen in de verhouding door hun grootste gemeenschappelijke deler. In ons voorbeeld van de appels en bananen (3:6), is de grootste gemeenschappelijke deler 3. Als we beide getallen door 3 delen, krijgen we de vereenvoudigde verhouding 1:2. Dit betekent dat er voor elke 1 appel, 2 bananen zijn. De proportie tussen appels en bananen blijft hetzelfde, alleen de getallen zijn kleiner.

Hoe bereken je een verhouding?

Het berekenen van een verhouding is eigenlijk heel eenvoudig. Volg deze stappen:

1. Identificeer de hoeveelheden: Bepaal welke hoeveelheden je met elkaar wilt vergelijken.
2. Noteer de hoeveelheden: Schrijf de hoeveelheden op in de juiste volgorde, gescheiden door een dubbele punt.
3. Vereenvoudig (indien mogelijk): Zoek de grootste gemeenschappelijke deler en deel alle getallen door deze deler.

Voorbeeld: Je hebt een klas met 20 leerlingen, waarvan 8 jongens en 12 meisjes. Wat is de verhouding tussen jongens en meisjes?

1. Identificeer de hoeveelheden: Jongens en meisjes
2. Noteer de hoeveelheden: 8:12
3. Vereenvoudig: De grootste gemeenschappelijke deler van 8 en 12 is 4. Dus, 8/4 = 2 en 12/4 = 3. De vereenvoudigde verhouding is 2:3.

De verhouding tussen jongens en meisjes is dus 2:3. Dit betekent dat er voor elke 2 jongens, 3 meisjes zijn.

Verhoudingen in recepten: Een smakelijk voorbeeld

Stel, je wilt een cake bakken. Het recept vereist een verhouding van 2:1 tussen bloem en suiker (bijvoorbeeld 2 kopjes bloem voor 1 kopje suiker). Wat als je meer cake wilt maken?

Als je de hoeveelheid bloem verdubbelt naar 4 kopjes, moet je ook de hoeveelheid suiker verdubbelen om de verhouding te behouden. Dus, je hebt 4 kopjes bloem en 2 kopjes suiker nodig. De verhouding blijft 2:1, maar de hoeveelheden zijn veranderd.

Belangrijk: Het is essentieel om de verhouding consistent te houden. Anders kan de cake droog, te zoet of gewoonweg mislukt zijn.

Verhoudingen en percentages: Een nauwe band

Verhoudingen en percentages zijn nauw met elkaar verbonden. Een percentage is eigenlijk een speciale verhouding die de waarde uitdrukt als een deel van 100. Om een verhouding om te zetten in een percentage, deel je het ene getal door het andere en vermenigvuldig je het resultaat met 100.

Voorbeeld: In de klas met 20 leerlingen zijn er 8 jongens. Wat is het percentage jongens in de klas?

1. Verhouding: 8 jongens op 20 leerlingen (8:20)
2. Delen: 8 / 20 = 0.4
3. Vermenigvuldigen met 100: 0.4 * 100 = 40%

Dus, 40% van de leerlingen in de klas is jongen.

Veelgemaakte fouten bij het berekenen van verhoudingen

Hoewel het berekenen van verhoudingen relatief eenvoudig is, worden er vaak fouten gemaakt. Hier zijn enkele veelvoorkomende fouten en hoe je ze kunt vermijden:

• Verkeerde volgorde: Zorg ervoor dat je de hoeveelheden in de juiste volgorde noteert. De verhouding 3:5 is anders dan de verhouding 5:3.
• Niet vereenvoudigen: Het is handig om de verhouding te vereenvoudigen, zodat je met kleinere en overzichtelijkere getallen werkt.
• Verkeerde eenheden: Controleer of de hoeveelheden in dezelfde eenheden zijn uitgedrukt. Je kunt bijvoorbeeld niet direct appels en kilo's appels met elkaar vergelijken.
• Vergeten te vermenigvuldigen bij percentages: Vergeet niet om het resultaat met 100 te vermenigvuldigen wanneer je een verhouding in een percentage wilt omzetten.

Wanneer verhoudingen complexer worden

Soms kom je verhoudingen tegen die complexer zijn, bijvoorbeeld wanneer je met drie of meer hoeveelheden tegelijk werkt. Het principe blijft hetzelfde, maar het vereenvoudigen kan iets lastiger zijn.

Voorbeeld: Een cocktail bestaat uit 2 delen rum, 3 delen sinaasappelsap en 1 deel grenadine. De verhouding is 2:3:1. Als je een grotere hoeveelheid cocktail wilt maken, moet je de hoeveelheden van alle ingrediënten in dezelfde verhouding verhogen.

De kritiek en nuance

Sommige mensen beweren dat een te sterke focus op verhoudingen de creativiteit kan belemmeren, vooral in contexten zoals koken of kunst. Ze vinden dat het blindelings volgen van recepten zonder na te denken over de smaakprofielen of de beschikbare ingrediënten kan leiden tot een minder bevredigend resultaat. Echter, het begrijpen van de basisverhoudingen vormt een stevige fundering. Zodra je de basis begrijpt, kun je experimenteren en je eigen draai aan dingen geven.

Het is belangrijk om te onthouden dat verhoudingen een hulpmiddel zijn, geen doel op zich. Ze helpen je om consistentie en evenwicht te bereiken, maar je moet ze niet als een rigide set regels beschouwen. Gebruik je intuïtie, experimenteer en pas de verhoudingen aan je eigen smaak en voorkeuren aan. De beste resultaten worden vaak bereikt door een combinatie van kennis en creativiteit.

Conclusie: Verhoudingen onder de knie

Het berekenen en begrijpen van verhoudingen is een waardevolle vaardigheid die je in veel aspecten van je leven kunt gebruiken. Van het aanpassen van recepten tot het beheren van je financiën, verhoudingen helpen je om betere beslissingen te nemen en problemen efficiënter op te lossen. Door de stappen in dit artikel te volgen en de veelgemaakte fouten te vermijden, kun je je vaardigheden op dit gebied verbeteren en met meer vertrouwen omgaan met cijfers.

Nu je de basisprincipes van verhoudingen begrijpt, daag ik je uit om ze in de praktijk te brengen. Probeer een recept aan te passen, je budget te analyseren, of de verhouding tussen verschillende aspecten van je leven te onderzoeken. Wat ga jij als eerste doen met je nieuwe kennis over verhoudingen?