Wat Is De Wortel Van

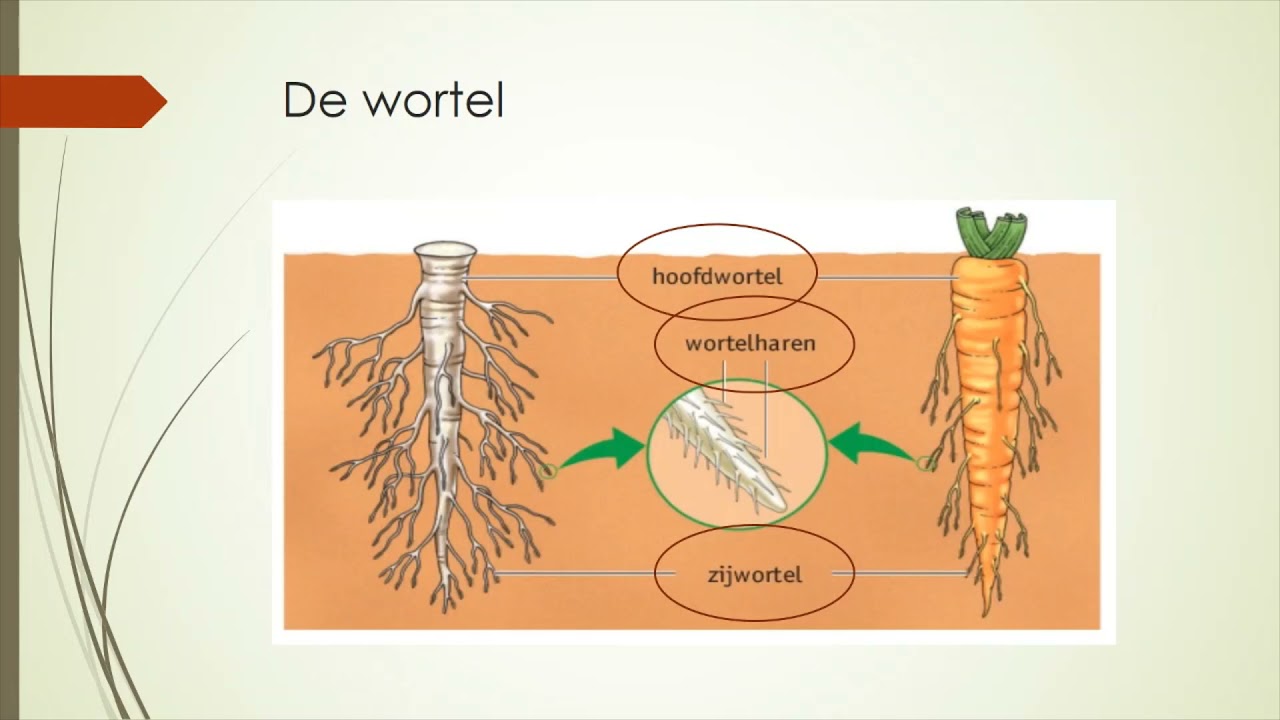
De wortel, in al zijn veelzijdigheid, is een concept dat diep verankerd zit in zowel de wiskunde als het dagelijks leven. Hoewel velen het misschien associëren met de bekende oranje groente, strekt de betekenis ervan zich veel verder uit. In dit artikel duiken we in de essentie van wat een wortel is, onthullen we de wiskundige principes erachter, en verkennen we hoe dit concept op onverwachte manieren in onze wereld opduikt.

De Wiskundige Wortel: Ontkracht de Macht

In de wiskunde is de wortel, en in het bijzonder de vierkantswortel, een operatie die het omgekeerde is van machtsverheffen. Simpel gezegd, als je een getal kwadrateert (verheft tot de macht 2), en vervolgens de vierkantswortel neemt van het resultaat, kom je terug bij het originele getal. Bijvoorbeeld: 5² = 25, en √25 = 5.

Definitie: De vierkantswortel van een getal *x* is een getal *y* zodanig dat *y² = x*.

Het symbool voor de vierkantswortel is √, afgeleid van de letter 'r' voor 'radix', Latijn voor 'wortel'. Het getal onder het wortelteken wordt het radicand genoemd.

Verschillende soorten wortels

Naast de vierkantswortel bestaan er ook andere soorten wortels, zoals de derdemachtswortel (kubuswortel), de vierdemachtswortel, enzovoort. De algemene formule voor een *n*-de machtswortel van een getal *x* is ⁿ√x. Dit betekent dat je een getal *y* zoekt zodanig dat *yⁿ = x*.

Bijvoorbeeld: De derdemachtswortel van 8 is 2 (³√8 = 2), omdat 2³ = 8.

Belangrijk om te onthouden: Het trekken van wortels van negatieve getallen leidt tot complexe getallen, een fascinerend gebied in de wiskunde dat buiten de scope van dit artikel valt, maar wel cruciaal is voor vele wetenschappelijke en technische toepassingen.

Eigenschappen van Wortels

Wortels hebben verschillende belangrijke eigenschappen die handig zijn bij het vereenvoudigen van expressies en het oplossen van vergelijkingen:

• Productregel: √(a * b) = √a * √b (de wortel van een product is het product van de wortels)
• Quotiëntregel: √(a / b) = √a / √b (de wortel van een quotiënt is het quotiënt van de wortels)
• Vereenvoudigen van wortels: Je kunt wortels vereenvoudigen door perfecte kwadraten (of kubussen, etc.) uit het radicand te halen. Bijvoorbeeld: √12 = √(4 * 3) = √4 * √3 = 2√3

Deze regels maken het mogelijk om complexe worteluitdrukkingen te manipuleren en te vereenvoudigen, wat essentieel is voor het oplossen van algebraïsche problemen.

Toepassingen in het Dagelijks Leven en de Wetenschap

Wortels zijn niet alleen abstracte wiskundige concepten; ze spelen een cruciale rol in diverse aspecten van ons dagelijks leven en de wetenschap.

Fysica

In de fysica kom je wortels tegen bij het berekenen van de snelheid, versnelling, en energie van objecten. Bijvoorbeeld, de formule voor de snelheid van een object dat valt onder invloed van de zwaartekracht bevat een vierkantswortel: v = √(2gh), waarbij *v* de snelheid is, *g* de gravitatieconstante, en *h* de hoogte.

Ook de periode van een slinger wordt berekend met een vierkantswortel: T = 2π√(L/g), waarbij *T* de periode is, *L* de lengte van de slinger, en *g* de gravitatieconstante.

Engineering

Ingenieurs gebruiken wortels bij het ontwerpen van bruggen, gebouwen, en andere constructies. Ze zijn essentieel bij het berekenen van de sterkte en stabiliteit van materialen en structuren.

Bijvoorbeeld, de stroomsterkte in een circuit kan worden berekend met behulp van de wet van Ohm, waarbij de wortel van het vermogen (P) over de weerstand (R) wordt genomen: I = √(P/R).

Financiën

In de financiële wereld worden wortels gebruikt bij het berekenen van rentevoeten, rendementen op investeringen, en de standaarddeviatie van een dataset. Bijvoorbeeld, de samengestelde rente kan worden berekend met een formule die een n-de machtswortel bevat.

Computer graphics

Computer graphics maken veel gebruik van wortels, vooral bij het berekenen van afstanden, reflecties, en brekingen van licht. De stelling van Pythagoras, die een vierkantswortel bevat, is fundamenteel voor 3D-modellering en rendering.

Data-analyse

In data-analyse, wordt de standaarddeviatie, een maat voor de spreiding van gegevens, berekend met behulp van een vierkantswortel. Dit is een cruciale statistische maat die helpt om de variabiliteit van een dataset te begrijpen.

Een Concreet Voorbeeld: De Afstand tussen Twee Punten

Een heel simpel voorbeeld is het berekenen van de afstand tussen twee punten in een tweedimensionaal vlak. Stel dat we de punten (x1, y1) en (x2, y2) hebben. De afstand *d* tussen deze punten wordt gegeven door de formule: d = √((x2 - x1)² + (y2 - y1)²). Deze formule is direct afgeleid van de stelling van Pythagoras, en illustreert hoe wortels worden gebruikt om geometrische afstanden te bepalen.

Het Belang van Begrip

Het begrijpen van de wortel is meer dan alleen het leren van een wiskundige operatie. Het is het ontwikkelen van een fundamenteel wiskundig inzicht dat je helpt om de wereld om je heen beter te begrijpen. Van het analyseren van data tot het ontwerpen van nieuwe technologieën, wortels zijn een onmisbaar hulpmiddel.

Hoewel het misschien in eerste instantie intimiderend lijkt, is het belangrijk om de tijd te nemen om de principes achter de wortel te begrijpen. Met oefening en toepassing zul je ontdekken dat het een krachtig en veelzijdig concept is dat je op vele manieren kan helpen.

Conclusie: De Wortel als Fundament

De wortel, zowel in de wiskundige als in de meer algemene betekenis, vertegenwoordigt een fundamentele bouwsteen van onze kennis en begrip van de wereld. Van de abstracte wiskunde tot de praktische toepassingen in de wetenschap, engineering, en het dagelijks leven, de wortel is overal aanwezig.

Aan de slag! Daag jezelf uit om de principes van wortels verder te verkennen. Oefen met het vereenvoudigen van worteluitdrukkingen, onderzoek hoe wortels worden gebruikt in de velden die je interesseren, en ontdek de schoonheid en kracht van dit fundamentele wiskundige concept. Want de wortel van succes ligt in een solide basis van begrip.