Wat Is De Wortel Van 12

Wiskunde, vaak gezien als een abstracte wetenschap, speelt een cruciale rol in ons dagelijks leven. Van het bouwen van bruggen tot het ontwikkelen van geavanceerde technologieën, wiskundige principes liggen aan de basis van veel van de structuren en systemen die we als vanzelfsprekend beschouwen. Een van de fundamentele concepten in de wiskunde is de wortel. In dit artikel duiken we dieper in de wortel van 12, onderzoeken we de eigenschappen ervan, en illustreren we de relevantie ervan met concrete voorbeelden.

Wat is een Wortel?

Eenvoudig gezegd is de wortel van een getal een waarde die, vermenigvuldigd met zichzelf (in het geval van een vierkantswortel), het oorspronkelijke getal oplevert. De vierkantswortel van een getal x wordt genoteerd als √x. Dus, als √x = y, dan betekent dit dat y * y = x.

Het begrip "wortel" kan ook verwijzen naar derdemachtswortels (∛x), vierdemachtswortels (⁴√x), en zo verder. In algemene termen spreekt men van de n-de machtswortel, waarbij n een positief geheel getal is.

Vierkantswortel van 12: Vereenvoudiging

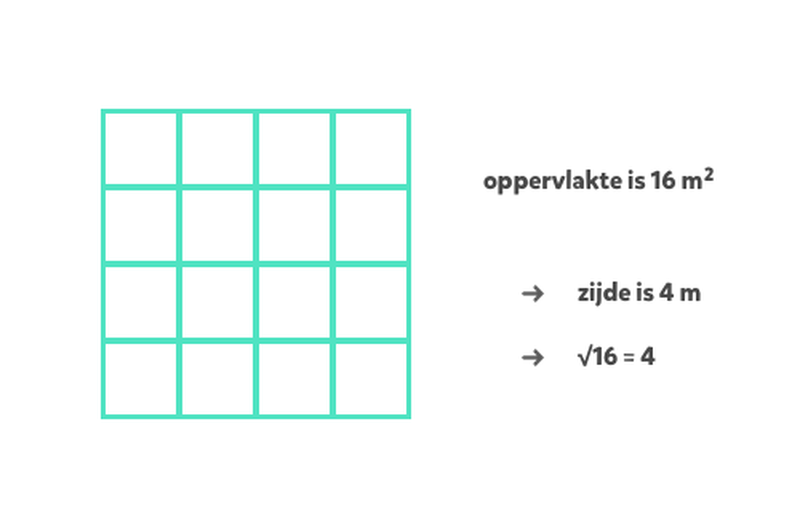
De vierkantswortel van 12 (√12) is het getal dat, vermenigvuldigd met zichzelf, 12 oplevert. Omdat 12 geen perfect vierkant is (d.w.z., er is geen geheel getal dat vermenigvuldigd met zichzelf 12 oplevert), is de vierkantswortel van 12 een irrationeel getal. Dit betekent dat de decimale representatie oneindig is en zich niet herhaalt.

Echter, we kunnen √12 vereenvoudigen. We zoeken naar perfecte vierkanten die delers zijn van 12. In dit geval is 4 een perfect vierkant (2*2 = 4) dat 12 deelt. We kunnen 12 dus schrijven als 4 * 3. Hierdoor kunnen we √12 herschrijven als volgt:

√12 = √(4 * 3) = √4 * √3 = 2√3

Dus, de vereenvoudigde vorm van de vierkantswortel van 12 is 2√3. Dit is de meest nauwkeurige weergave, hoewel een decimale benadering vaak bruikbaar is in praktische toepassingen.

Decimale Benadering en Berekening

Om een decimale benadering van 2√3 te vinden, hebben we een benadering van √3 nodig. √3 is ongeveer 1.732. Daarom:

2√3 ≈ 2 * 1.732 ≈ 3.464

De vierkantswortel van 12 is dus ongeveer 3.464. Je kunt dit eenvoudig controleren door 3.464 * 3.464 te berekenen, wat dicht bij 12 ligt (iets meer dan 12, vanwege de afronding).

Vroeger werden vierkantswortels vaak berekend met behulp van tabellen of algoritmen zoals de "staartdeling" methode. Tegenwoordig gebruiken we meestal een rekenmachine of een computerprogramma om de waarde van wortels te berekenen.

Toepassingen van Wortels in de Praktijk

Wortels zijn niet alleen abstracte wiskundige concepten; ze hebben talloze praktische toepassingen in verschillende disciplines.

Geometrie en Architectuur

In de geometrie worden wortels gebruikt om afstanden te berekenen, met name bij het toepassen van de stelling van Pythagoras. Bijvoorbeeld, als een rechthoekige driehoek zijden heeft van lengte a en b, dan is de lengte van de schuine zijde (c) gelijk aan √(a² + b²).

In de architectuur worden wortels gebruikt bij het ontwerpen van gebouwen, het berekenen van afmetingen en het bepalen van de stabiliteit van structuren. Bij het ontwerpen van een koepel of een boog spelen wortels een essentiële rol bij het berekenen van de benodigde materialen en de belasting die de structuur kan dragen.

Voorbeeld: Stel je voor dat je een vierkant terras wilt aanleggen met een oppervlakte van 12 vierkante meter. Om de lengte van één zijde van het terras te bepalen, moet je de vierkantswortel van 12 berekenen (√12 ≈ 3.464 meter). Je zou dan elke zijde van het terras ongeveer 3.464 meter lang maken.

Natuurkunde en Engineering

In de natuurkunde komen wortels voor in formules die de snelheid, versnelling en energie van objecten beschrijven. De kinetische energie (KE) van een object met massa m en snelheid v wordt bijvoorbeeld gegeven door KE = ½mv². Om de snelheid te berekenen als je de kinetische energie en massa kent, moet je de vierkantswortel nemen: v = √(2KE/m).

In de engineering worden wortels gebruikt bij het ontwerpen van machines, het analyseren van trillingen en het berekenen van de sterkte van materialen. Bijvoorbeeld, bij het ontwerpen van een brug, moeten ingenieurs de krachten en spanningen op de structuur berekenen. Deze berekeningen omvatten vaak het gebruik van wortels om de veiligheidsmarges te bepalen en ervoor te zorgen dat de brug bestand is tegen de verwachte belastingen.

Financiën en Statistiek

In de financiën worden wortels gebruikt bij het berekenen van de standaarddeviatie, een maat voor de spreiding van een set gegevens. De standaarddeviatie is de vierkantswortel van de variantie.

In de statistiek worden wortels gebruikt in verschillende statistische tests en modellen. Bijvoorbeeld, bij het berekenen van betrouwbaarheidsintervallen wordt vaak de vierkantswortel van de steekproefvariantie gebruikt.

Voorbeeld: Stel dat je de investeringsrisico's wilt analyseren. De standaarddeviatie van de rendementen van een belegging kan worden berekend met behulp van wortels. Een hogere standaarddeviatie duidt op een hoger risico.

Computerwetenschappen en Cryptografie

In de computerwetenschappen worden wortels gebruikt in algoritmen voor beeldverwerking, 3D-modellering en simulaties.

In de cryptografie, een gebied dat zich bezighoudt met veilige communicatie, worden wortels gebruikt in complexe wiskundige operaties die de basis vormen van encryptie-algoritmen. Bijvoorbeeld, het berekenen van discrete logaritmen, een probleem dat moeilijk op te lossen is, wordt gebruikt in sommige cryptografische systemen.

Waarom is het Belangrijk om Wortels te Begrijpen?

Het begrijpen van wortels is essentieel om verschillende redenen:

Probleemoplossing: Wortels stellen ons in staat om problemen op te lossen in verschillende disciplines, van geometrie tot financiën.
Analytisch denken: Het werken met wortels vereist analytisch denken en het vermogen om complexe problemen te vereenvoudigen.
Fundamentele kennis: Wortels vormen een fundamenteel onderdeel van de wiskundige basis die nodig is voor geavanceerdere studies in wetenschap, technologie, engineering en wiskunde (STEM).
Praktische toepassingen: Zoals we hebben gezien, hebben wortels talloze praktische toepassingen in het dagelijks leven en in professionele contexten.

Conclusie

De vierkantswortel van 12, hoewel een irrationeel getal, is cruciaal in verschillende wiskundige en praktische contexten. Door √12 te vereenvoudigen tot 2√3 en de decimale benadering (ongeveer 3.464) te begrijpen, kunnen we dit concept toepassen op echte problemen in de geometrie, natuurkunde, financiën en andere disciplines. Het begrijpen van wortels is een essentiële vaardigheid voor iedereen die zich bezighoudt met wetenschap, technologie, engineering of wiskunde. Of je nu een student bent, een professional, of gewoon iemand die geïnteresseerd is in de wereld om je heen, het beheersen van de basisprincipes van wortels zal je analytische vaardigheden verbeteren en je in staat stellen om problemen effectiever op te lossen.

Actie: Daag jezelf uit! Probeer andere wortels te vereenvoudigen, zoals √18, √27 of √50. Onderzoek hoe wortels worden gebruikt in een vakgebied dat je interesseert. Blijf leren en ontdek de kracht van wiskunde!