Wat Is Een Geheel Getal

Heb je je ooit afgevraagd wat er precies bedoeld wordt met de term "geheel getal"? Misschien heb je het op school geleerd, maar de betekenis is vervaagd, of je bent simpelweg nieuwsgierig. Geen zorgen, je bent niet de enige! Wiskunde kan soms intimiderend lijken, met al die definities en regels. Maar het concept van een geheel getal is eigenlijk heel eenvoudig en speelt een cruciale rol in ons dagelijks leven.

We gaan samen op onderzoek uit om dit concept te ontrafelen, te begrijpen waarom het zo belangrijk is en te zien hoe het overal om ons heen opduikt. Laten we eerlijk zijn: wiskundige termen klinken soms droog en theoretisch. Maar we zullen proberen om het zo praktisch en relevant mogelijk te maken.

Wat is een Geheel Getal precies?

Een geheel getal is simpelweg een getal zonder breuken of decimalen. Dat betekent dat het een compleet getal is, zonder "stukjes" eraan vast. Het omvat alle positieve getallen (1, 2, 3, ...), alle negatieve getallen (-1, -2, -3, ...), en nul (0). Denk er aan als treden op een ladder: je kunt niet op een halve trede staan, je staat op een hele trede. Dat is het idee achter gehele getallen.

Voorbeelden van gehele getallen: -5, -1, 0, 3, 100, 1000
Voorbeelden van niet-gehele getallen: 2.5, -1.7, 1/2, √2

Zie je het verschil? De niet-gehele getallen hebben allemaal een 'rest' na de komma, of zijn een breuk. Gehele getallen zijn solide, complete eenheden.

Waarom zijn Gehele Getallen Belangrijk?

Je vraagt je misschien af: "Oké, ik weet nu wat het is, maar waarom is het belangrijk?". Het antwoord is dat gehele getallen de basis vormen van veel wiskundige en praktische toepassingen in ons dagelijks leven.

Praktische Toepassingen in het Dagelijks Leven

Denk aan de volgende situaties:

Tellen: Het aantal appels in een mand, het aantal stoelen in een kamer, het aantal mensen in een bus. Je kunt geen halve appel tellen, toch?
Geld: Je kunt een geheel aantal euro's bezitten. Hoewel je centen hebt (decimalen), tel je in hele euro's. Zelfs schulden worden uitgedrukt in gehele getallen (bijvoorbeeld -50 euro).
Temperatuur: Temperaturen worden vaak uitgedrukt in gehele getallen (bijvoorbeeld 20 graden Celsius, -5 graden Celsius).
Verdiepingen in een gebouw: Je kunt op de eerste, tweede, of derde verdieping zijn, maar niet op de 2.5e verdieping (tenzij er een hele rare constructie is!).

Zoals je ziet, zijn gehele getallen onmisbaar om dingen te kwantificeren en te begrijpen in de wereld om ons heen. Ze vormen de basis voor alledaagse berekeningen en metingen.

Wiskundige Fundamenten

Gehele getallen zijn ook essentieel in meer geavanceerde wiskunde:

Algebra: Veel algebraïsche vergelijkingen en problemen vereisen het werken met gehele getallen.
Getaltheorie: Dit is een tak van de wiskunde die zich specifiek bezighoudt met de eigenschappen van gehele getallen.
Computerwetenschappen: Computers gebruiken gehele getallen om data op te slaan en te verwerken. Bitrepresentaties zijn gebaseerd op 0 en 1, wat gehele getallen zijn.

De Rol van Nul (0)

Nul is een speciaal geval binnen de gehele getallen. Het vertegenwoordigt afwezigheid of niets. Het is het neutrale element voor optellen (a + 0 = a). Hoewel het soms verwarrend kan zijn, is nul cruciaal voor ons getalsysteem.

Negatieve Gehele Getallen

Negatieve getallen zijn getallen kleiner dan nul. Ze worden gebruikt om tekorten, schulden, temperaturen onder nul, en andere situaties te representeren waarin iets "minder dan niets" is.

Denk aan een bankrekening. Als je €100 hebt en vervolgens €150 uitgeeft, heb je een saldo van -€50. Die -€50 is een negatief geheel getal.

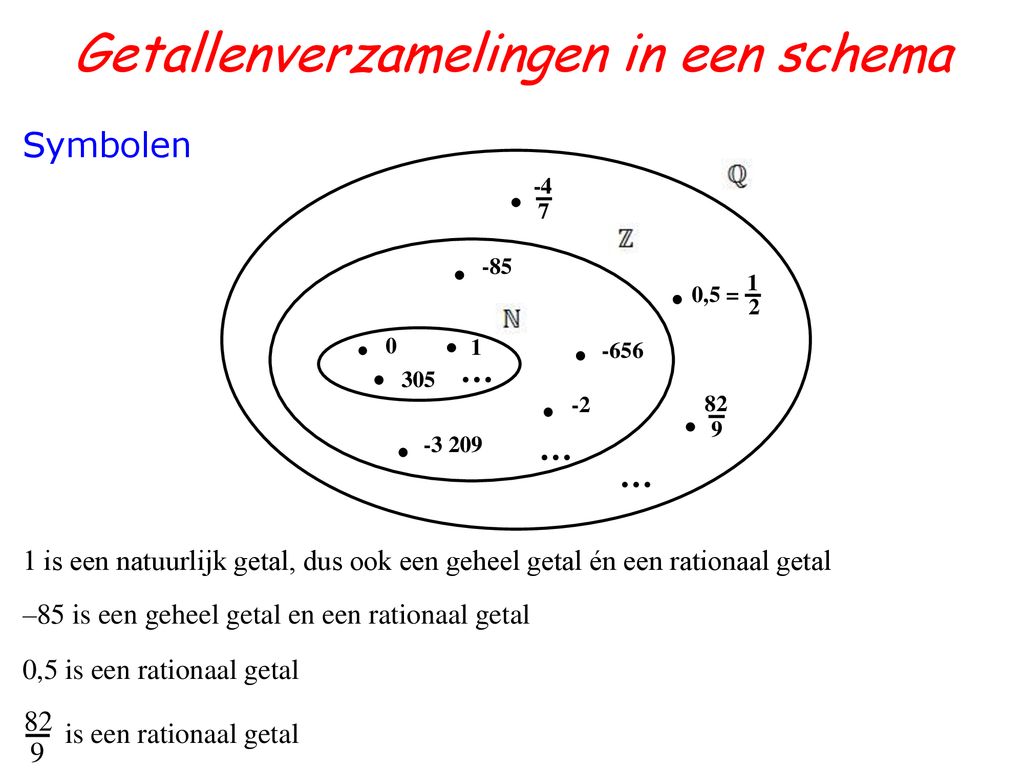
Gehele Getallen vs. Andere Getallen

Het is belangrijk om het verschil te begrijpen tussen gehele getallen en andere soorten getallen:

Rationale Getallen: Dit zijn getallen die kunnen worden uitgedrukt als een breuk (p/q), waarbij p en q gehele getallen zijn en q niet gelijk is aan nul. Gehele getallen zijn een subset van rationale getallen (bijvoorbeeld 3 kan worden geschreven als 3/1).
Irrationale Getallen: Dit zijn getallen die niet als een breuk kunnen worden uitgedrukt (bijvoorbeeld π, √2).
Reële Getallen: Dit omvat alle rationale en irrationale getallen.

Om het simpel te zeggen: alle gehele getallen zijn rationale getallen en reële getallen, maar niet alle rationale of reële getallen zijn gehele getallen.

Veelgemaakte Misvattingen

Er zijn een paar veelvoorkomende misvattingen over gehele getallen:

"Gehele getallen zijn alleen positief." Dit is niet waar. Gehele getallen omvatten positieve getallen, negatieve getallen en nul.
"Nul is geen getal." Nul is absoluut een getal en een cruciaal element van de gehele getallen.
"Breuken zijn gehele getallen." Breuken zijn rationale getallen, maar geen gehele getallen tenzij ze kunnen worden vereenvoudigd tot een geheel getal (bijvoorbeeld 4/2 = 2).

Counterpoints en Kritiek

Hoewel het concept van gehele getallen relatief eenvoudig is, zijn er situaties waarin de definities complexer kunnen worden in hogere wiskunde. Sommige takken van de wiskunde, zoals de complexe analyse, werken met getallen die een reëel en imaginair deel hebben, waardoor de eenvoudige definitie van een "geheel getal" minder relevant wordt.

Echter, voor de meeste praktische toepassingen en voor het fundamentele begrip van wiskunde, is de definitie die we hier hebben besproken voldoende en accuraat.

Het Belang van een Goed Begrip

Een solide basis in gehele getallen is essentieel voor succes in verdere wiskundestudies en in veel praktische aspecten van het leven. Het helpt je om logisch te denken, problemen op te lossen en de wereld om je heen beter te begrijpen.

Zonder een goed begrip van gehele getallen zou het lastig zijn om simpele taken uit te voeren zoals budgetteren, recepten volgen, of zelfs de tijd lezen. Het is de fundering waarop complexere wiskundige concepten zijn gebouwd.

Conclusie

We hebben nu gezien wat een geheel getal is, waarom het belangrijk is en hoe het in ons dagelijks leven opduikt. Het is een fundamenteel concept dat de basis vormt voor veel meer complexe wiskundige ideeën. Begrijpen wat een geheel getal is, is dus cruciaal voor je wiskundige ontwikkeling en je vermogen om de wereld om je heen te begrijpen.

Hopelijk heeft deze uitleg de term "geheel getal" minder intimiderend gemaakt en je geholpen om de relevantie ervan in te zien. Het is meer dan alleen een wiskundige definitie; het is een fundamenteel onderdeel van hoe we de wereld kwantificeren en begrijpen.

Nu, met deze nieuwe kennis, denk eens na: waar kom jij vandaag nog gehele getallen tegen in je dagelijks leven?