Wat Is Een Periodiek Verband

We leven in een wereld vol patronen en herhalingen. Van de seizoenen die jaarlijks terugkeren tot de getijden die dagelijks eb en vloed vertonen. Achter veel van deze verschijnselen schuilt een periodiek verband. Maar wat houdt dit precies in? In dit artikel duiken we diep in het concept van periodieke verbanden, verkennen we hun kenmerken en illustreren we hun aanwezigheid in verschillende aspecten van ons leven.

Wat is een Periodiek Verband?

Een periodiek verband is een wiskundige relatie waarin een bepaalde waarde zich na een vaste tijdsperiode herhaalt. Dit betekent dat een functie, een proces, of een gebeurtenis na een bepaalde interval, de periode, terugkeert naar zijn oorspronkelijke staat. Deze herhaling maakt het mogelijk om het gedrag in de toekomst te voorspellen, gebaseerd op de waarnemingen in het verleden.

Kenmerken van een Periodiek Verband

Om een periodiek verband te herkennen, zijn er een aantal sleutelkenmerken waar we op moeten letten:

• Herhaling: De meest fundamentele eigenschap. De waarde van de functie of gebeurtenis herhaalt zich na een bepaalde periode.
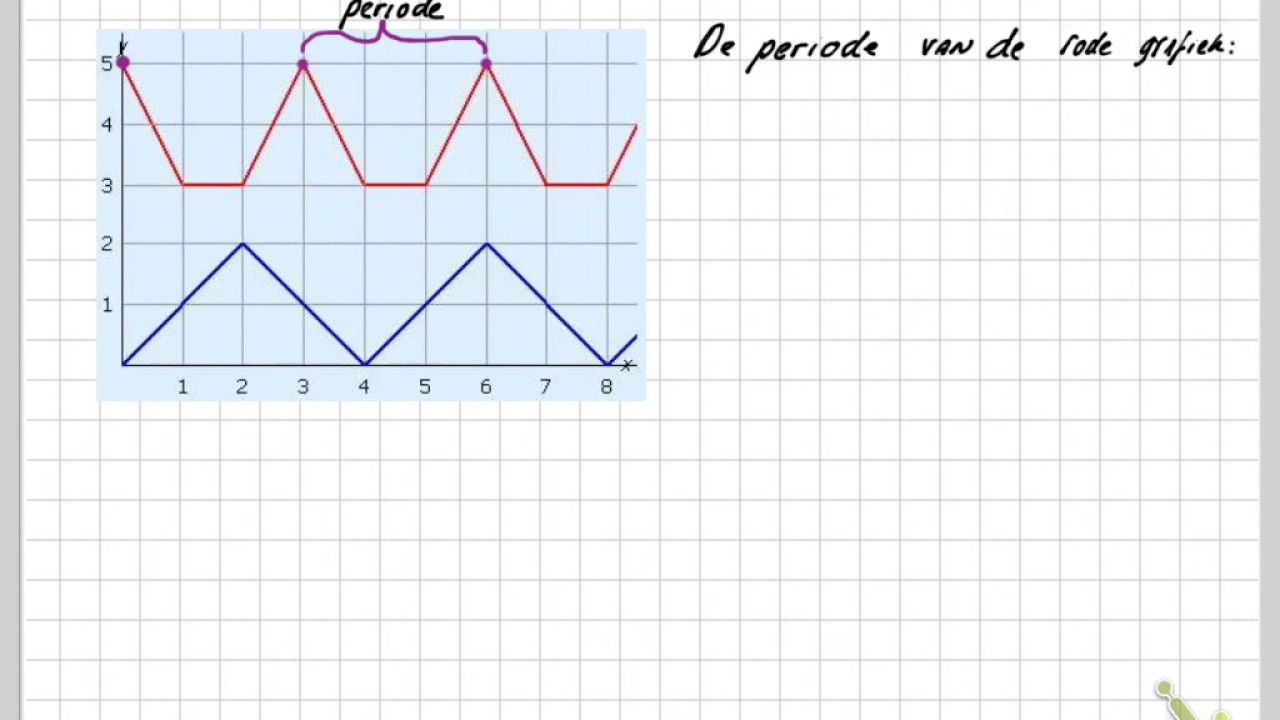
• Periode (T): De vaste tijdseenheid waarna de herhaling plaatsvindt.
• Amplitude: De maximale afwijking van de evenwichtsstand. Dit is relevant bij oscillerende systemen zoals golven.
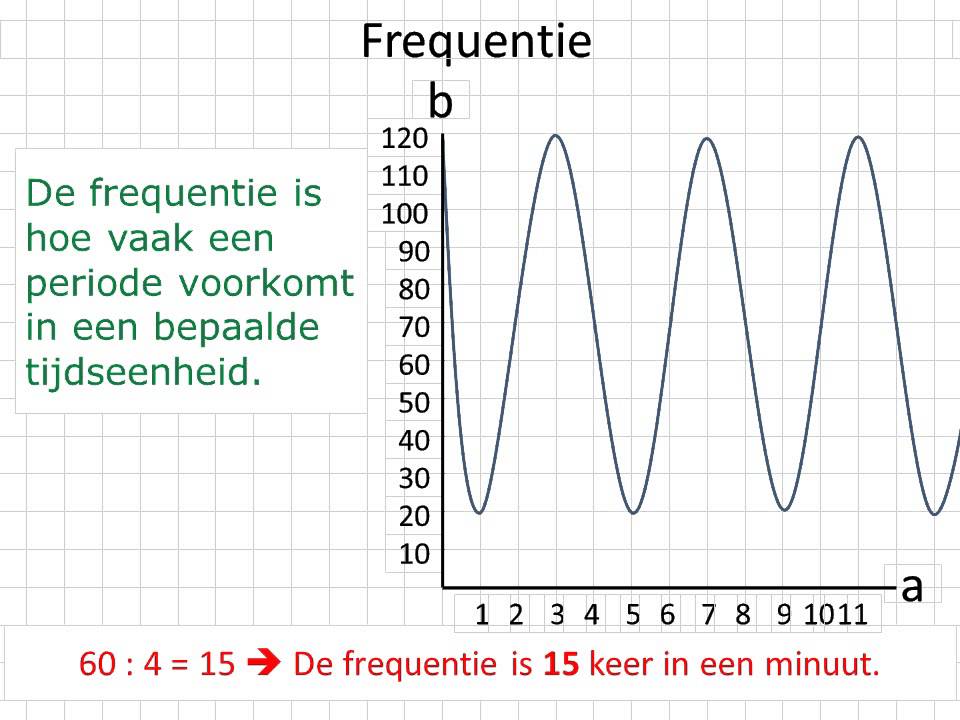
• Frequentie (f): Het aantal herhalingen per tijdseenheid. De frequentie is de inverse van de periode (f = 1/T).

Deze kenmerken stellen ons in staat om periodieke verbanden te kwantificeren en te beschrijven met behulp van wiskundige formules, grafieken en modellen.

Wiskundige Beschrijving van Periodieke Verbanden

Periodieke verbanden kunnen wiskundig worden beschreven met behulp van periodieke functies. De meest bekende voorbeelden zijn de sinus- en cosinusfuncties. Deze functies beschrijven een perfecte, continue oscillatie en vormen de basis voor het modelleren van vele periodieke verschijnselen.

De algemene vorm van een sinusfunctie is:

y = A * sin(ωt + φ)

Waar:

• A de amplitude is.
• ω de hoekfrequentie is (ω = 2πf).
• t de tijd is.
• φ de faseverschuiving is, die de positie van de golf op t=0 bepaalt.

Andere periodieke functies zijn bijvoorbeeld de tangensfunctie en zaagtandgolven. Complexe periodieke signalen kunnen vaak worden ontleed in een som van sinus- en cosinusfuncties, een techniek die bekend staat als Fourier-analyse.

Voorbeelden van Periodieke Verbanden in de Praktijk

Periodieke verbanden komen overal om ons heen voor. Hier zijn enkele concrete voorbeelden:

De Seizoenen

De cyclus van de seizoenen (lente, zomer, herfst, winter) is een duidelijk voorbeeld van een periodiek verband. De periode is één jaar. De temperatuur, de hoeveelheid daglicht en de vegetatie vertonen een duidelijke jaarlijkse herhaling. Dit periodieke verband wordt veroorzaakt door de helling van de aardas en de rotatie van de aarde rond de zon.

De Getijden

De getijden, eb en vloed, zijn het gevolg van de zwaartekracht van de maan en de zon. De periode van de getijden varieert, maar is typisch ongeveer 12 uur en 25 minuten voor semi-diurnale getijden (twee keer eb en vloed per dag). De waterstand vertoont een duidelijke herhaling, waardoor scheepvaart en kustecosystemen sterk beïnvloed worden.

Hartslag

De hartslag is een periodiek proces waarbij het hart samentrekt en ontspant om bloed door het lichaam te pompen. De periode is de tijd tussen twee opeenvolgende hartslagen. De frequentie van de hartslag, oftewel het aantal slagen per minuut, is een belangrijke indicator voor de gezondheid.

Elektrische Wisselstroom (AC)

In de elektriciteitsnetwerken wordt wisselstroom (AC) gebruikt. De spanning en stroom variëren sinusvormig in de tijd. In Europa is de frequentie van de wisselstroom 50 Hz, wat betekent dat de spanning 50 keer per seconde van richting verandert. Dit periodieke gedrag is essentieel voor de werking van veel elektrische apparaten.

Geluid

Geluid is een trilling in de lucht. Een zuivere toon wordt beschreven door een sinusgolf. De frequentie van de golf bepaalt de toonhoogte van het geluid. Muziekinstrumenten produceren complexere geluidsgolven die periodiek zijn, maar bestaan uit meerdere frequenties.

Data-analyse en Periodieke Verbanden

In de data-analyse worden periodieke verbanden gebruikt om patronen te herkennen en voorspellingen te doen. Tijdreeksanalyse is een veelgebruikte techniek om periodieke componenten in data te identificeren. Bijvoorbeeld, de verkoop van ijs kan een jaarlijks periodiek patroon vertonen, met een piek in de zomermaanden. Door dit patroon te begrijpen, kunnen bedrijven hun voorraadbeheer optimaliseren.

Voorbeeld Data: Stel je voor dat je de dagelijkse temperaturen over een jaar meet. Deze data kan worden geanalyseerd om de jaarlijkse periodieke trend (de seizoenen) en eventuele afwijkingen te identificeren. Software zoals Python met libraries als Pandas en Matplotlib maakt het eenvoudig om deze data te visualiseren en analyseren.

Periodieke verbanden worden ook gebruikt in de financiële wereld om aandelenkoersen en economische indicatoren te analyseren. Hoewel aandelenkoersen niet perfect periodiek zijn, kunnen er bepaalde cyclische patronen aanwezig zijn die beleggers proberen te benutten.

Conclusie

Periodieke verbanden zijn fundamenteel voor het begrijpen van de wereld om ons heen. Van de natuurlijke cycli zoals de seizoenen en de getijden tot de technologische toepassingen zoals elektriciteit en geluid, periodieke verschijnselen spelen een cruciale rol. Door de kenmerken van periodieke verbanden te begrijpen en ze wiskundig te modelleren, kunnen we patronen herkennen, voorspellingen doen en onze omgeving beter beheersen.

Verder onderzoek: Ben je geïnteresseerd geraakt in periodieke verbanden? Duik dieper in de Fourier-analyse, leer meer over tijdreeksanalyse in de economie, of onderzoek hoe muziekinstrumenten werken. De mogelijkheden zijn eindeloos! Het herkennen en begrijpen van periodieke patronen opent deuren naar een dieper begrip van onze wereld.