Wat Is Een Recht Evenredig Verband

In de wereld van de wiskunde en de natuurwetenschappen komen we vaak relaties tegen tussen verschillende grootheden. Eén van de meest fundamentele en bruikbare relaties is de recht evenredig verband. Dit concept, hoewel eenvoudig in zijn basisvorm, heeft een enorme impact op hoe we de wereld om ons heen begrijpen en voorspellen. Dit artikel duikt diep in wat een recht evenredig verband precies is, hoe je het kunt herkennen, en waar je het in de praktijk tegenkomt.

Wat is een Recht Evenredig Verband?

Een recht evenredig verband, ook wel proportioneel verband genoemd, beschrijft een relatie tussen twee variabelen waarbij de ene variabele een constante vermenigvuldiging is van de andere. Met andere woorden, als de ene variabele toeneemt, neemt de andere variabele ook toe met een vaste factor. En als de ene afneemt, neemt de andere ook af, eveneens met diezelfde vaste factor.

Wiskundig gezien kunnen we dit uitdrukken als:

y = kx

Waar:

y de afhankelijke variabele is.
x de onafhankelijke variabele is.
k de proportionaliteitsconstante is (ook wel de evenredigheidsconstante genoemd).

De proportionaliteitsconstante k vertegenwoordigt de verhouding tussen y en x. Het is een cruciaal element in een recht evenredig verband, omdat het de mate van de verandering definieert. Als k bijvoorbeeld 2 is, betekent dit dat voor elke toename van 1 in x, y toeneemt met 2.

Kenmerken van een Recht Evenredig Verband

Om een recht evenredig verband te herkennen, zijn er een paar belangrijke kenmerken waar je op kunt letten:

Lineariteit: De grafiek van een recht evenredig verband is een rechte lijn. Dit is een direct gevolg van de lineaire vergelijking y = kx.
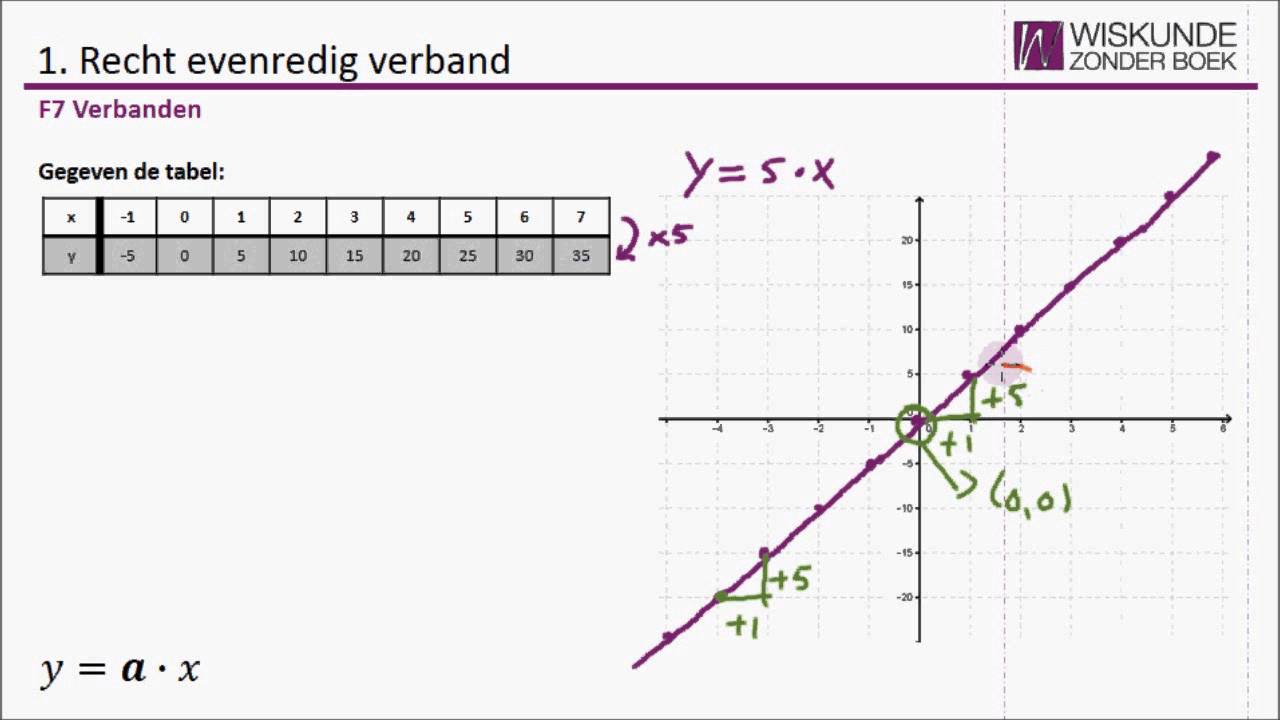
Oorsprong: De rechte lijn gaat altijd door de oorsprong (0, 0) van het assenstelsel. Dit komt omdat als x gelijk is aan 0, y ook gelijk is aan 0 (y = k * 0 = 0).
Constante Verhouding: De verhouding tussen y en x (y/x) is altijd constant en gelijk aan k. Dit is de meest fundamentele eigenschap.

Hoe Herken je een Recht Evenredig Verband in de Praktijk?

In de praktijk is het niet altijd direct duidelijk of er sprake is van een recht evenredig verband. Hier zijn een paar stappen die je kunt volgen om het te onderzoeken:

Verzamel Data: Zorg voor een set van waarden voor zowel de onafhankelijke variabele (x) als de afhankelijke variabele (y).
Bereken de Verhouding: Deel voor elk paar waarden y door x (y/x).
Analyseer de Resultaten: Als de verhouding (y/x) ongeveer constant is voor alle paren waarden, dan is er waarschijnlijk sprake van een recht evenredig verband. Kleine afwijkingen kunnen voorkomen door meetfouten of afrondingen.
Maak een Grafiek: Plot de data op een grafiek. Als de punten een rechte lijn vormen die door de oorsprong gaat, dan is dat een sterke indicatie van een recht evenredig verband.

Voorbeelden van Recht Evenredige Verbanden

Recht evenredige verbanden komen overal om ons heen voor. Hier zijn een paar concrete voorbeelden:

1. Afstand en Tijd (bij constante snelheid)

Als je met een constante snelheid rijdt, is de afstand die je aflegt recht evenredig met de tijd die je reist. De proportionaliteitsconstante k is in dit geval de snelheid. Bijvoorbeeld, als je met een snelheid van 80 km/uur rijdt, geldt:

Afstand = 80 * Tijd

Dus, na 2 uur heb je 160 km afgelegd (80 * 2 = 160), en na 3 uur heb je 240 km afgelegd (80 * 3 = 240).

2. Kosten en Aantal Producten (bij gelijke prijs per product)

Als je een bepaald product koopt met een vaste prijs per stuk, dan zijn de totale kosten recht evenredig met het aantal producten dat je koopt. De proportionaliteitsconstante k is in dit geval de prijs per product. Bijvoorbeeld, als een appel €0,50 kost, geldt:

Totale Kosten = 0,50 * Aantal Appels

Dus, 5 appels kosten €2,50 (0,50 * 5 = 2,50), en 10 appels kosten €5,00 (0,50 * 10 = 5,00).

3. Massa en Volume (bij constante dichtheid)

Voor een bepaalde stof met een constante dichtheid is de massa recht evenredig met het volume. De proportionaliteitsconstante k is in dit geval de dichtheid van de stof. Bijvoorbeeld, als de dichtheid van water 1 g/cm³ is, geldt:

Massa = 1 * Volume

Dus, 10 cm³ water heeft een massa van 10 gram, en 50 cm³ water heeft een massa van 50 gram.

4. De Wet van Ohm

In de elektriciteit beschrijft de Wet van Ohm een recht evenredig verband tussen de stroom (I) door een weerstand en de spanning (V) over de weerstand, mits de weerstand (R) constant is. De formule luidt:

V = I * R

Hier is de weerstand (R) de proportionaliteitsconstante. Als je de weerstand constant houdt, dan is de spanning recht evenredig met de stroom.

Data en Analyse

Laten we een hypothetisch voorbeeld bekijken met data over de hoeveelheid verkochte ijsjes en de bijbehorende winst:

Aantal Ijsjes Verkocht (x)	Winst (€) (y)
10	25
20	50
30	75
40	100

Laten we de verhouding y/x berekenen voor elk paar waarden:

10 ijsjes: 25/10 = 2,5
20 ijsjes: 50/20 = 2,5
30 ijsjes: 75/30 = 2,5
40 ijsjes: 100/40 = 2,5

We zien dat de verhouding constant is en gelijk is aan 2,5. Dit betekent dat de winst recht evenredig is met het aantal verkochte ijsjes, en de proportionaliteitsconstante k is 2,5. Dus, voor elk verkocht ijsje wordt er €2,50 winst gemaakt.

Belang van het Recht Evenredig Verband

Het recht evenredig verband is van groot belang om verschillende redenen:

Vereenvoudiging: Het vereenvoudigt complexe relaties tot een eenvoudig te begrijpen formule.
Voorspelling: Het stelt ons in staat om waarden te voorspellen. Als we de proportionaliteitsconstante kennen, kunnen we de waarde van de afhankelijke variabele berekenen voor elke waarde van de onafhankelijke variabele.
Fundamenteel Principe: Het is een fundamenteel principe in veel wetenschappelijke en technische disciplines.
Modelvorming: Het wordt gebruikt om modellen te bouwen die de werkelijkheid benaderen en voorspellingen mogelijk maken.

Conclusie

Een recht evenredig verband is een essentieel concept in de wiskunde en de wetenschap. Het beschrijft een eenvoudige, maar krachtige relatie tussen twee variabelen waarbij de ene een constante vermenigvuldiging is van de andere. Door de kenmerken van een recht evenredig verband te begrijpen, kun je het herkennen in de praktijk en het gebruiken om voorspellingen te doen en problemen op te lossen.

De volgende keer dat je patronen ziet in de data, denk dan aan het recht evenredig verband. Oefen met het herkennen van deze verbanden in de wereld om je heen, en je zult merken dat je de complexiteit van de wereld beter begrijpt. Probeer bijvoorbeeld zelf data te verzamelen en te analyseren om te zien of er sprake is van een recht evenredig verband tussen verschillende variabelen. Dit is een uitstekende manier om je begrip van dit concept te verdiepen en je analytische vaardigheden te verbeteren.