Wat Is Het Kwadraat Van

Heb je je ooit afgevraagd hoe wiskundigen complexe problemen oplossen? Soms is het antwoord verrassend eenvoudig en gebaseerd op een fundamenteel concept: het kwadraat. Of je nu worstelt met algebra, geometrie, of gewoon nieuwsgierig bent naar wiskunde, het begrijpen van het kwadraat is cruciaal. Misschien heb je er in de les over gehoord, maar de toepassing en betekenis ervan ontging je. Geen zorgen, in dit artikel gaan we dieper in op de vraag: "Wat is het kwadraat van…?"

Wat is een Kwadraat?

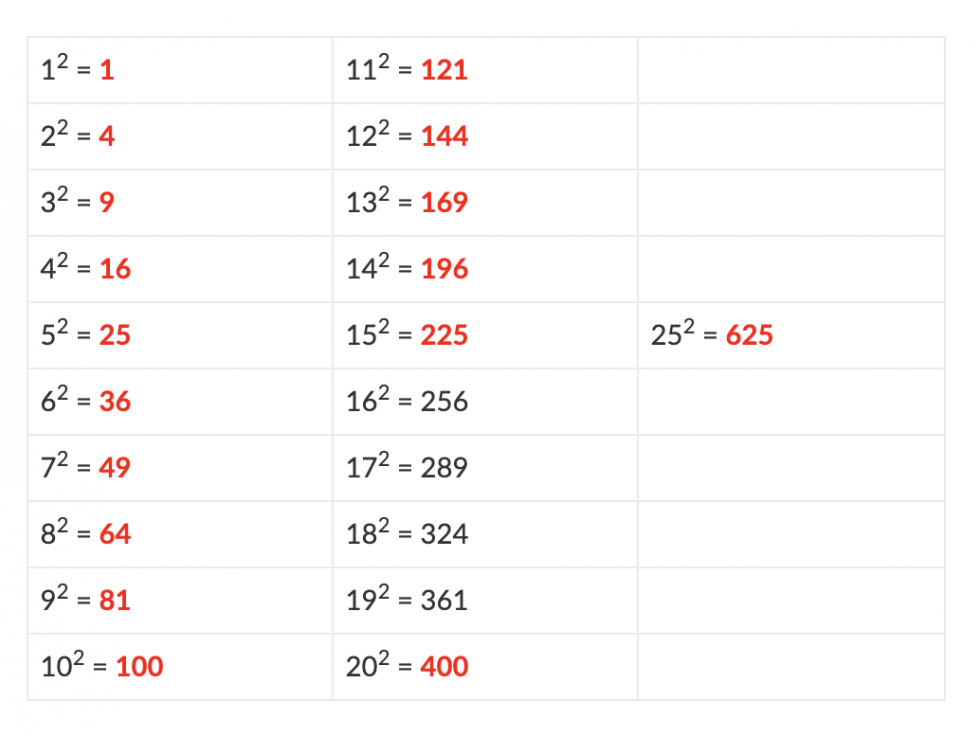
Laten we beginnen bij de basis. Het kwadraat van een getal is het resultaat van het vermenigvuldigen van dat getal met zichzelf. Met andere woorden, je neemt een getal en je doet het keer zichzelf. In wiskundige notatie wordt dit weergegeven als x², waarbij x het getal is dat we kwadrateren.

Simpel gezegd: het kwadraat van 5 is 5 * 5 = 25. Het kwadraat van 10 is 10 * 10 = 100. Je ziet, het is geen hogere wiskunde, maar de impact ervan is enorm.

Waarom is Kwadrateren Belangrijk?

Je vraagt je wellicht af, "Waarom zou ik dit moeten weten?". Kwadrateren is meer dan alleen een wiskundige operatie. Het duikt op in allerlei gebieden van wetenschap, technologie, en het dagelijks leven.

Denk bijvoorbeeld aan:

Oppervlakteberekeningen: De oppervlakte van een vierkant wordt berekend door de zijde te kwadrateren.
De Stelling van Pythagoras: In een rechthoekige driehoek is het kwadraat van de schuine zijde gelijk aan de som van de kwadraten van de andere twee zijden (a² + b² = c²).
Natuurkunde: Veel formules in de natuurkunde, zoals de formule voor kinetische energie (E_k = 1/2 * mv²), bevatten kwadraten.
Statistiek: Bij het berekenen van de variantie en standaarddeviatie, belangrijke maatstaven voor de spreiding van data, wordt kwadrateren gebruikt.

Zoals je ziet, is de toepassing breed en gevarieerd. Zonder kennis van kwadrateren zouden veel van deze berekeningen onmogelijk zijn.

Hoe Bereken je een Kwadraat?

De meest directe manier om een kwadraat te berekenen is door het getal eenvoudigweg met zichzelf te vermenigvuldigen. Echter, afhankelijk van het getal en de beschikbare hulpmiddelen, zijn er verschillende methoden die je kunt gebruiken.

Handmatig Vermenigvuldigen: Voor kleinere getallen is dit de meest voor de hand liggende methode.
Rekenmachine: De meeste rekenmachines hebben een speciale knop voor het kwadrateren (meestal aangeduid als x²).
Excel of Google Sheets: In spreadsheets kun je de formule "=A1^2" gebruiken om het kwadraat van de waarde in cel A1 te berekenen.
Programmeren: In programmeertalen zoals Python kun je de operator "**" gebruiken om te kwadrateren (bijvoorbeeld 5**2).

Kwadraten van Negatieve Getallen

Een belangrijk punt om te onthouden is dat het kwadraat van een negatief getal altijd positief is. Dit komt omdat een negatief getal vermenigvuldigd met een negatief getal een positief resultaat oplevert.

Bijvoorbeeld:

Het kwadraat van -3 is (-3) * (-3) = 9.
Het kwadraat van -10 is (-10) * (-10) = 100.

Dit is een cruciaal concept, vooral bij het oplossen van vergelijkingen en het werken met complexe getallen.

Praktische Voorbeelden en Toepassingen

Laten we eens kijken naar een paar praktische voorbeelden om het concept van kwadrateren te verduidelijken:

Voorbeeld 1: Een vierkant stuk land

Stel je voor dat je een vierkant stuk land hebt met een zijde van 15 meter. Om de oppervlakte van dit land te berekenen, moet je de zijde kwadrateren.

Oppervlakte = zijde * zijde = 15 meter * 15 meter = 225 vierkante meter.

Voorbeeld 2: De Stelling van Pythagoras

Een ladder staat tegen een muur. De ladder is 5 meter lang en de afstand van de voet van de ladder tot de muur is 3 meter. Hoe hoog reikt de ladder op de muur?

We kunnen de stelling van Pythagoras gebruiken: a² + b² = c²

Waarbij c de lengte van de ladder is (5 meter) en a de afstand van de voet van de ladder tot de muur is (3 meter). We willen b (de hoogte op de muur) vinden.

3² + b² = 5²

9 + b² = 25

b² = 25 - 9

b² = 16

b = √16 = 4 meter

De ladder reikt dus 4 meter hoog op de muur.

Voorbeeld 3: Berekenen van de remweg

De remweg van een auto is ruwweg evenredig met het kwadraat van de snelheid. Dus als je snelheid verdubbelt, wordt je remweg ongeveer vier keer zo lang! Dit is een belangrijk veiligheidsaspect om in gedachten te houden.

Veelgemaakte Fouten en Hoe Ze te Vermijden

Er zijn een paar veelgemaakte fouten bij het werken met kwadraten die je moet vermijden:

Verwarring met verdubbelen: Het kwadraat van een getal is niet hetzelfde als het getal verdubbelen. Het kwadraat van 5 is 25, terwijl het dubbele van 5 10 is.
Vergeten de tekens: Zoals eerder vermeld, is het kwadraat van een negatief getal altijd positief. Vergeet dit niet!
Foutieve invoer in de rekenmachine: Controleer altijd of je de juiste knop gebruikt (x²) en of je het getal correct hebt ingevoerd.

Kwadraat versus Vierkantswortel

Het is essentieel om het verschil te begrijpen tussen het kwadraat en de vierkantswortel van een getal. Zoals we hebben gezien, is het kwadraat het resultaat van het vermenigvuldigen van een getal met zichzelf.

De vierkantswortel daarentegen is het getal dat, vermenigvuldigd met zichzelf, het oorspronkelijke getal oplevert. Het is dus de inverse operatie van het kwadrateren.

Bijvoorbeeld:

Het kwadraat van 9 is 81.
De vierkantswortel van 81 is 9.

Het symbool voor de vierkantswortel is √. Dus √81 = 9.

Het is cruciaal om deze twee concepten uit elkaar te houden, omdat ze vaak in dezelfde problemen voorkomen.

Conclusie

Het kwadraat van een getal is een fundamenteel concept in de wiskunde met brede toepassingen in de wetenschap, technologie en het dagelijks leven. Door te begrijpen wat het is, hoe je het berekent, en hoe het zich verhoudt tot andere concepten zoals de vierkantswortel, kun je je wiskundige vaardigheden aanzienlijk verbeteren en je inzicht in de wereld om je heen vergroten.

Dus, de volgende keer dat je de term "kwadraat" hoort, weet je precies wat er mee bedoeld wordt. En wie weet, misschien kun je het zelfs gebruiken om een probleem op te lossen of een nieuwe uitdaging aan te gaan!