Wie Bedacht De Bekende Wiskundige Stelling 10 Letters

Heeft u zich ooit afgevraagd wie de briljante geest was achter een van de meest fundamentele stellingen in de wiskunde? De stelling die we hier behandelen, wordt in het Nederlands omschreven als een "bekende wiskundige stelling" van 10 letters. Het antwoord leidt ons naar een fascinerende figuur uit de oudheid: Pythagoras.

Dit artikel is bedoeld voor iedereen die geïnteresseerd is in wiskunde, geschiedenis, of gewoon nieuwsgierig is naar de oorsprong van concepten die we dagelijks, vaak onbewust, gebruiken. We duiken in het leven en werk van Pythagoras, onderzoeken de stelling zelf en ontkrachten enkele misvattingen die erover bestaan.

Pythagoras: Meer dan alleen een Stelling

Pythagoras, geboren rond 570 v.Chr. op het Griekse eiland Samos, was veel meer dan alleen een wiskundige. Hij was een filosoof, een mysticus en een leider van een religieuze broederschap. Zijn invloed reikte veel verder dan de abstracte wereld van getallen en formules.

Een Leven van Reizen en Leren

Pythagoras reisde intensief door de antieke wereld, onder andere naar Egypte en Babylonië. Deze reizen stelden hem in staat om kennis te vergaren over wiskunde, astronomie en religie. Men gelooft dat hij in Egypte werd ingewijd in mysteriegodsdiensten en dat hij daar de basis legde voor zijn latere filosofische en wiskundige ideeën. De Babylonische wiskunde, met hun geavanceerde kennis van getallen en meetkunde, was ook een belangrijke inspiratiebron.

De Pythagoreïsche Broederschap

Na zijn reizen vestigde Pythagoras zich in Croton (het huidige Crotone) in Zuid-Italië, waar hij een broederschap stichtte. Deze broederschap, bekend als de Pythagoreïsche school, was een gemeenschap van volgelingen die hun leven wijdden aan de studie van wiskunde, filosofie en muziek. De Pythagoreërs geloofden dat alles in het universum kon worden uitgedrukt in getallen en dat de studie van wiskunde de sleutel was tot het begrijpen van de kosmos. Ze waren een soort wetenschappelijke gemeenschap, maar ook een religieuze sekte met strikte regels en rituelen.

De Stelling van Pythagoras: De Kern van de Zaak

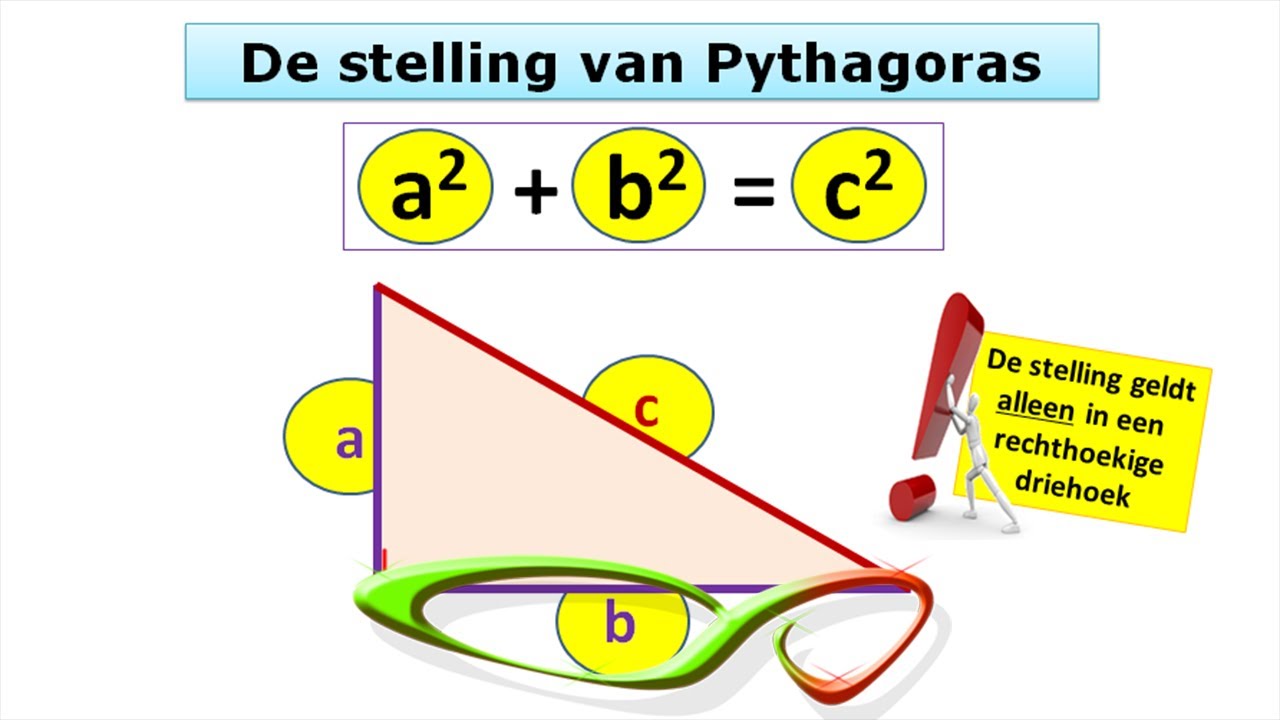
De stelling van Pythagoras stelt dat in een rechthoekige driehoek (een driehoek met een hoek van 90 graden), het kwadraat van de lengte van de schuine zijde (de zijde tegenover de rechte hoek) gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden. In formulevorm: a² + b² = c², waarbij a en b de lengtes van de rechthoekszijden zijn en c de lengte van de schuine zijde.

Voorbeelden en Toepassingen

Deze ogenschijnlijk eenvoudige stelling heeft talloze toepassingen in de wiskunde, natuurkunde, engineering en zelfs in het dagelijks leven. Enkele voorbeelden:

• Navigatie: Het bepalen van afstanden en posities met behulp van triangulatie.
• Architectuur: Het berekenen van de lengte van diagonale steunen in gebouwen.
• Bouwkunde: Het uitzetten van rechte hoeken bij het bouwen van funderingen.
• Computer graphics: Het berekenen van afstanden tussen punten op een scherm.

Stel je bijvoorbeeld voor dat je een ladder tegen een muur wilt plaatsen. De muur en de grond vormen een rechte hoek. Met de stelling van Pythagoras kun je berekenen hoe lang de ladder moet zijn om een bepaalde hoogte op de muur te bereiken, gegeven de afstand van de voet van de ladder tot de muur.

Wie Bedacht het Nu Echt? De Controversie

Hoewel de stelling bekend staat als de stelling van Pythagoras, is het belangrijk op te merken dat het idee erachter al veel eerder bekend was bij andere beschavingen, zoals de Babyloniërs en de Egyptenaren. Archeologische vondsten, zoals de Babylonische kleitablet Plimpton 322 (daterend van rond 1800 v.Chr.), tonen aan dat de Babyloniërs al bekend waren met Pythagoreïsche drietallen (sets van gehele getallen die voldoen aan de vergelijking a² + b² = c²). De Egyptenaren gebruikten mogelijk de verhouding 3:4:5 om rechte hoeken uit te zetten bij het bouwen van piramides.

Dus, waarom wordt de stelling dan aan Pythagoras toegeschreven? Het antwoord ligt in het feit dat Pythagoras en zijn volgelingen waarschijnlijk de eersten waren die een algemeen bewijs voor de stelling formuleerden. Ze waren niet alleen in staat om specifieke voorbeelden te vinden, maar ook om een logisch argument te leveren dat aantoonde dat de stelling voor alle rechthoekige driehoeken geldt. Dit is een cruciaal verschil tussen empirische observatie en wiskundig bewijs.

Bewijzen van de Stelling

Er zijn honderden verschillende bewijzen voor de stelling van Pythagoras. Een van de bekendste is het bewijs door dissectie, waarbij je de oppervlakte van vierkanten gebouwd op de zijden van de rechthoekige driehoek herschikt om te laten zien dat de oppervlakte van het vierkant op de schuine zijde gelijk is aan de som van de oppervlakten van de vierkanten op de rechthoekszijden. Andere bewijzen maken gebruik van algebraïsche manipulaties of geometrische argumenten.

Misvattingen en Feiten

Er bestaan een aantal misvattingen over de stelling van Pythagoras:

• Misvatting: De stelling geldt voor alle driehoeken. Feit: De stelling geldt alleen voor rechthoekige driehoeken.
• Misvatting: De stelling is bedacht door Pythagoras zelf. Feit: Het idee was al bekend bij andere beschavingen, maar Pythagoras en zijn volgelingen leverden waarschijnlijk het eerste algemene bewijs.
• Misvatting: De stelling is alleen nuttig in de wiskunde. Feit: De stelling heeft talloze toepassingen in de praktijk, van navigatie tot architectuur.

De Erfenis van Pythagoras

De stelling van Pythagoras is een hoeksteen van de wiskunde en een fundamenteel concept dat in vele disciplines wordt gebruikt. De invloed van Pythagoras reikt echter verder dan alleen de wiskunde. Zijn filosofische ideeën over de rol van getallen in het universum hebben een diepe invloed gehad op de ontwikkeling van de wetenschap en de cultuur.

De Pythagoreïsche broederschap was een van de eerste wetenschappelijke gemeenschappen en hun benadering van kennisvergaring, gebaseerd op observatie, experiment en logisch redeneren, heeft de basis gelegd voor de moderne wetenschappelijke methode. Hoewel veel van de details van Pythagoras' leven en werk in nevelen gehuld zijn, is zijn erfenis onmiskenbaar. Hij was een visionair denker die de wereld om hem heen probeerde te begrijpen door middel van wiskunde en filosofie.

Dus, de volgende keer dat u de stelling van Pythagoras gebruikt om een probleem op te lossen, denk dan eens aan de Pythagoras, de man achter de stelling. Hij was meer dan alleen een wiskundige; hij was een filosoof, een mysticus en een pionier die een blijvende impact op de wereld heeft gehad.

Het begrijpen van de geschiedenis en de context van wiskundige concepten, zoals de stelling van Pythagoras, kan onze waardering voor de wiskunde verdiepen en ons helpen om de relevantie ervan in ons dagelijks leven te zien. Wiskunde is niet alleen een abstracte verzameling formules en regels, maar een krachtig hulpmiddel om de wereld om ons heen te begrijpen en te navigeren.