Hoe Bereken Je De Straal Van Een Cirkel

Herken je dat? Je bent bezig met een project, misschien wel een klus in huis, een wiskundeopdracht, of je ontwerpt iets. Plotseling stuit je op een cirkel en heb je de straal nodig. Maar... hoe bereken je die straal eigenlijk? Geen zorgen, je bent niet de enige! Veel mensen worstelen hiermee. Het goede nieuws is: het is helemaal niet zo ingewikkeld als het lijkt. Deze gids helpt je stap voor stap de straal van een cirkel te berekenen, ongeacht de informatie die je hebt.

Waarom is dit belangrijk? De straal van een cirkel is een fundamentele waarde in veel disciplines. Van architectuur en engineering tot kunst en design, en zelfs in dagelijkse situaties zoals het bepalen van de juiste maat voor een taartvorm. Het begrijpen van hoe je de straal berekent, opent deuren naar een dieper begrip van de wereld om ons heen.

Verschillende Methoden om de Straal te Berekenen

Er zijn verschillende manieren om de straal van een cirkel te berekenen, afhankelijk van wat je al weet. We bespreken de meest voorkomende methoden:

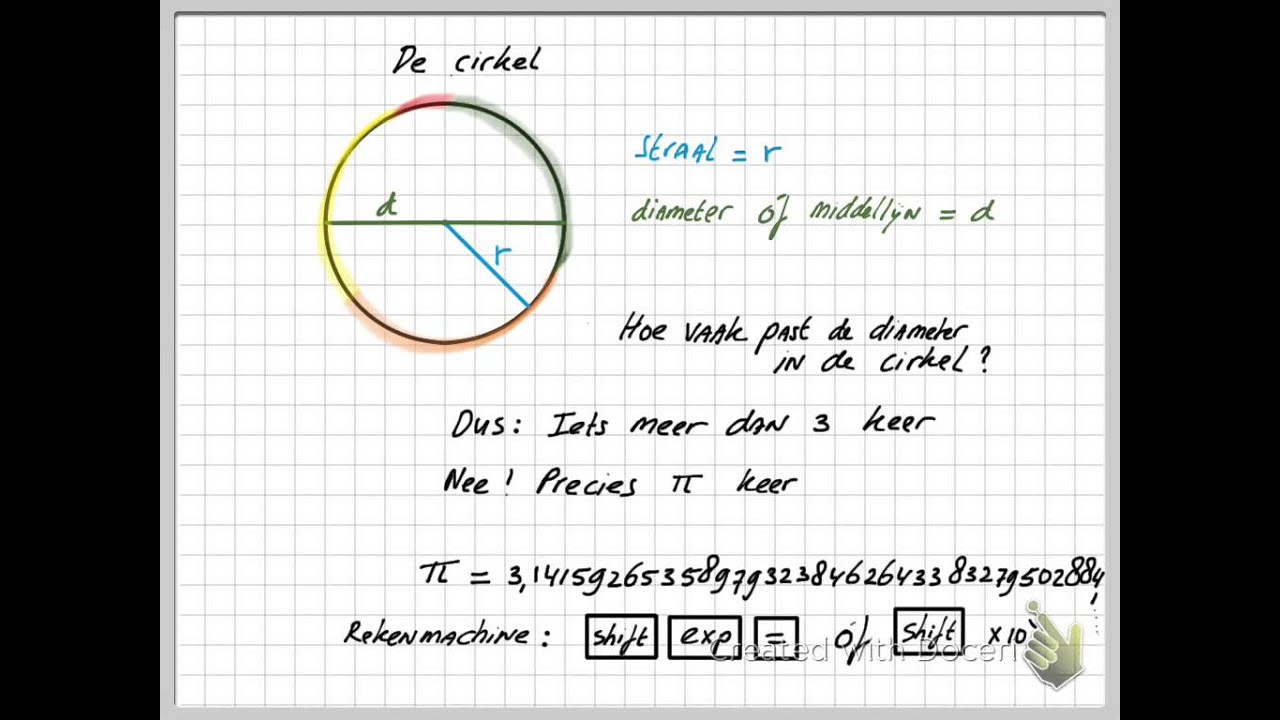
1. De Straal Berekenen vanuit de Diameter

Dit is de meest eenvoudige methode. De diameter van een cirkel is de afstand van de ene kant van de cirkel naar de andere, die door het middelpunt gaat. De straal is de helft van de diameter. Dus:

Straal = Diameter / 2

Voorbeeld: Stel dat de diameter van een cirkel 10 cm is. Dan is de straal 10 cm / 2 = 5 cm.

2. De Straal Berekenen vanuit de Omtrek

De omtrek van een cirkel is de afstand rondom de cirkel. De formule voor de omtrek is:

Omtrek = 2 * π * Straal

Waarbij π (pi) een constante is, ongeveer gelijk aan 3.14159.

Om de straal te berekenen vanuit de omtrek, herschrijven we de formule:

Straal = Omtrek / (2 * π)

Voorbeeld: Stel dat de omtrek van een cirkel 25 cm is. Dan is de straal 25 cm / (2 * 3.14159) ≈ 3.98 cm.

Let op: Het is belangrijk om een rekenmachine met een π-toets te gebruiken voor een zo nauwkeurig mogelijk resultaat.

3. De Straal Berekenen vanuit de Oppervlakte

De oppervlakte van een cirkel is de ruimte die de cirkel inneemt. De formule voor de oppervlakte is:

Oppervlakte = π * Straal²

Om de straal te berekenen vanuit de oppervlakte, herschrijven we de formule:

Straal = √(Oppervlakte / π)

Het teken √(x) betekent de vierkantswortel van x.

Voorbeeld: Stel dat de oppervlakte van een cirkel 50 cm² is. Dan is de straal √(50 cm² / 3.14159) ≈ 3.99 cm.

4. De Straal Berekenen met een Middelpunt en een Punt op de Cirkel

Als je de coördinaten van het middelpunt van de cirkel (x₁, y₁) en de coördinaten van een punt op de cirkel (x₂, y₂) kent, kun je de straal berekenen met de afstandsformule:

Straal = √((x₂ - x₁)² + (y₂ - y₁)² )

Dit is in feite de stelling van Pythagoras toegepast om de afstand tussen de twee punten te berekenen.

Voorbeeld: Stel dat het middelpunt van de cirkel (1, 2) is en een punt op de cirkel (4, 6) is. Dan is de straal √((4 - 1)² + (6 - 2)²) = √(3² + 4²) = √(9 + 16) = √25 = 5.

Waarom Verschillende Methoden?

Je vraagt je misschien af: waarom zijn er zoveel methoden? Het antwoord is simpel: je hebt niet altijd alle informatie over een cirkel. Soms ken je de diameter, soms de omtrek, en soms de oppervlakte. Elke methode is geschikt voor een specifieke situatie. Het is belangrijk om te begrijpen welke methode je moet gebruiken op basis van de gegevens die je hebt.

Mogelijke Uitdagingen en Hoe Ze te Overwinnen

Soms loop je tegen problemen aan bij het berekenen van de straal. Hier zijn enkele veelvoorkomende uitdagingen en oplossingen:

• Onnauwkeurige metingen: Gebruik nauwkeurige meetinstrumenten en meet meerdere keren om fouten te minimaliseren.
• Onvolledige informatie: Als je niet genoeg informatie hebt, probeer dan meer gegevens te verzamelen of een andere methode te gebruiken.
• Verkeerde formules: Zorg ervoor dat je de juiste formules gebruikt en dat je de eenheden correct converteert.
• Rekenfouten: Controleer je berekeningen zorgvuldig en gebruik een rekenmachine om fouten te voorkomen.

Counterpoints: Is de Straal Echt Zo Belangrijk?

Sommigen beweren dat de focus op de straal overdreven is. Ze stellen dat andere eigenschappen van de cirkel, zoals de diameter of de omtrek, net zo belangrijk zijn. Hoewel dit waar is, is de straal vaak de basis voor verdere berekeningen en ontwerpen. De straal is een fundamentele bouwsteen en het begrijpen ervan is essentieel voor het werken met cirkels.

Een ander argument is dat in moderne CAD-programma's de software de berekeningen automatisch uitvoert. Dit is zeker waar, maar het begrijpen van de principes achter de berekeningen stelt je in staat om de software effectiever te gebruiken en om fouten te herkennen en te corrigeren.

De Impact in de Praktijk

Laten we eens kijken naar een paar voorbeelden van hoe de berekening van de straal wordt gebruikt in de praktijk:

• Architectuur: Architecten gebruiken de straal om bogen, koepels en andere ronde structuren te ontwerpen.
• Engineering: Ingenieurs gebruiken de straal om tandwielen, wielen en andere mechanische onderdelen te ontwerpen.
• Design: Designers gebruiken de straal om logo's, patronen en andere visuele elementen te creëren.
• Koken: Bepalen van de juiste maat voor een taartvorm of pizzabodem.
• Navigatie: Het berekenen van afstanden op kaarten, vooral wanneer gebruik wordt gemaakt van kompassen en gradenbogen.

Deze voorbeelden laten zien dat de berekening van de straal een breed toepassingsgebied heeft en een essentiële vaardigheid is in veel verschillende vakgebieden.

Een Oefening: De Straal Zelf Berekenen

Laten we nu een eenvoudige oefening doen. Stel je voor dat je een ronde tafel wilt maken. Je hebt een stuk hout met een omtrek van 3 meter. Wat is de straal van de tafel die je kunt maken?

Gebruik de formule: Straal = Omtrek / (2 * π)

Straal = 3 meter / (2 * 3.14159) ≈ 0.477 meter.

Dus, je kunt een tafel maken met een straal van ongeveer 0.477 meter.

Conclusie

De straal van een cirkel is een belangrijke waarde die je op veel verschillende manieren kunt berekenen. Door de verschillende methoden te begrijpen en te oefenen, kun je de straal berekenen, ongeacht de informatie die je hebt. Het is een vaardigheid die je helpt in diverse situaties, van alledaagse klusjes tot complexe ontwerpen.

Waar ga jij de kennis over het berekenen van de straal voor gebruiken? Welk project inspireert je nu je dit weet?