Hoe Bereken Je Een Hoek Van Een Driehoek

Heb je je ooit afgevraagd hoe landmeters precies hoeken bepalen voor een nieuw gebouw, of hoe piloten hun koers nauwkeurig bepalen? Het antwoord ligt vaak in de geometrie, en meer specifiek, in de principes van driehoeken. Misschien denk je nu: "Driehoeken? Dat is toch iets van school?" Ja, dat klopt! Maar het begrijpen van hoe je de hoeken van een driehoek berekent, is een fundamentele vaardigheid die verrassend vaak van pas komt, zowel in het dagelijks leven als in meer gespecialiseerde vakgebieden.

Veel mensen worstelen met wiskunde, en geometrie in het bijzonder. De formules lijken ingewikkeld, en het is soms lastig te zien hoe het allemaal samenhangt. Maar vrees niet! Dit artikel is ontworpen om je op een duidelijke en toegankelijke manier te helpen de hoeken van een driehoek te berekenen. We breken de theorie af en geven je praktische tips en voorbeelden. Laten we beginnen!

De Basisprincipes van Driehoeken

Voordat we in de berekeningen duiken, is het belangrijk de basisprincipes van driehoeken te begrijpen. Een driehoek is een gesloten figuur met drie zijden en drie hoeken. En hier komt een cruciaal feit: de som van de hoeken in elke driehoek is altijd 180 graden. Dit is een fundamentele regel die we constant zullen gebruiken.

Er zijn verschillende soorten driehoeken, elk met hun eigen specifieke kenmerken:

• Gelijkzijdige driehoek: Alle drie zijden zijn even lang, en alle drie hoeken zijn 60 graden.
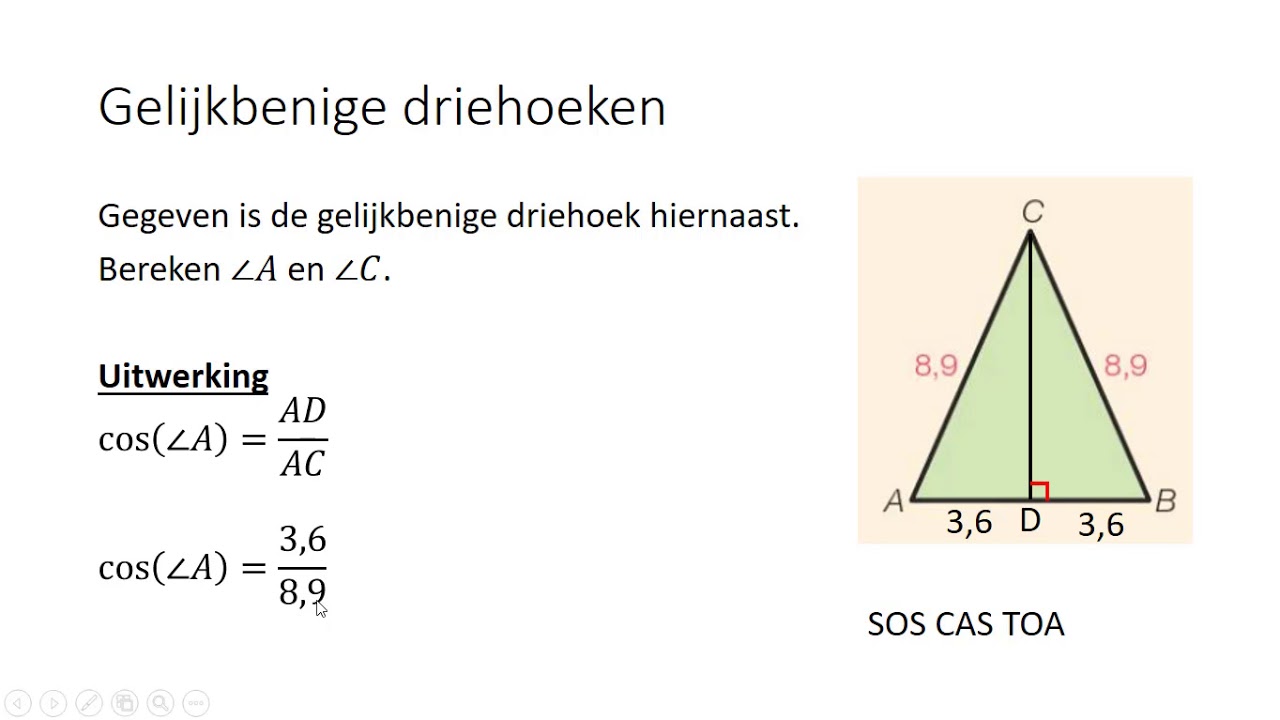
• Gelijkbenige driehoek: Twee zijden zijn even lang, en de hoeken tegenover die zijden zijn gelijk.
• Ongelijkzijdige driehoek: Alle drie zijden zijn verschillend, en alle drie hoeken zijn verschillend.
• Rechthoekige driehoek: Heeft één hoek van 90 graden (een rechte hoek).
• Scherphoekige driehoek: Alle hoeken zijn kleiner dan 90 graden.
• Stomphoekige driehoek: Heeft één hoek groter dan 90 graden.

Het herkennen van het type driehoek kan je helpen bij het kiezen van de juiste methode om de hoeken te berekenen. Bijvoorbeeld, als je weet dat je met een rechthoekige driehoek te maken hebt, weet je al één hoek (90 graden), en dat maakt de berekening van de andere twee hoeken een stuk eenvoudiger.

Verschillende Methoden om Hoeken te Berekenen

Er zijn verschillende methoden om de hoeken van een driehoek te berekenen, afhankelijk van de informatie die je hebt. Laten we de meest gebruikte methoden bekijken:

1. De Som van de Hoeken Regel

Zoals eerder vermeld, is de som van de hoeken in elke driehoek 180 graden. Dit is de meest eenvoudige en vaakst gebruikte methode. Als je de waarde van twee hoeken kent, kun je de derde hoek berekenen door ze van 180 graden af te trekken.

Voorbeeld: Stel dat je een driehoek hebt waarbij hoek A 60 graden is en hoek B 80 graden. Om hoek C te vinden, doe je: Hoek C = 180 - 60 - 80 = 40 graden.

2. De Sinusregel

De sinusregel is handig als je de lengte van ten minste één zijde en de tegenoverliggende hoek kent, en de lengte van een andere zijde of de waarde van een andere hoek. De sinusregel stelt dat de verhouding tussen de lengte van een zijde en de sinus van de tegenoverliggende hoek constant is voor alle zijden en hoeken in een driehoek.

De formule is: a / sin(A) = b / sin(B) = c / sin(C), waarbij a, b en c de lengtes van de zijden zijn, en A, B en C de tegenoverliggende hoeken.

Voorbeeld: Stel dat je weet dat zijde a = 10 cm, hoek A = 30 graden, en zijde b = 15 cm. Om hoek B te vinden, gebruik je de sinusregel: 10 / sin(30) = 15 / sin(B). Je lost dit op voor sin(B) en neemt vervolgens de inverse sinus (arcsin) om de waarde van hoek B te vinden.

Belangrijk: Je hebt een wetenschappelijke rekenmachine nodig om de sinus en inverse sinus te berekenen.

3. De Cosinusregel

De cosinusregel is nuttig in twee scenario's:

• Je kent de lengte van alle drie zijden en wilt een hoek berekenen.
• Je kent de lengte van twee zijden en de ingesloten hoek (de hoek tussen die twee zijden) en wilt de lengte van de derde zijde berekenen (hoewel dit artikel zich richt op hoekberekeningen, is het nuttig om de hele cosinusregel te begrijpen).

De formule is: a² = b² + c² - 2bc * cos(A), waarbij a, b en c de lengtes van de zijden zijn, en A is de hoek tegenover zijde a.

Om hoek A te berekenen als je alle drie zijden kent, kun je de formule herschrijven als: cos(A) = (b² + c² - a²) / (2bc). Vervolgens neem je de inverse cosinus (arccos) om de waarde van hoek A te vinden.

Voorbeeld: Stel dat a = 8 cm, b = 5 cm en c = 7 cm. Om hoek A te berekenen: cos(A) = (5² + 7² - 8²) / (2 * 5 * 7) = (25 + 49 - 64) / 70 = 10 / 70 = 1/7. Je neemt de arccos van 1/7 om hoek A te vinden.

Nogmaals: Een wetenschappelijke rekenmachine is essentieel voor het berekenen van de inverse cosinus.

4. Specifieke Methoden voor Rechthoekige Driehoeken

Rechthoekige driehoeken zijn speciaal omdat je al één hoek kent (90 graden). Dit maakt de berekening van de andere hoeken eenvoudiger. Naast de som van de hoeken regel, kun je ook de trigonometrische functies sinus, cosinus en tangens gebruiken (vaak afgekort als sin, cos en tan).

Deze functies definiëren de verhoudingen tussen de zijden van een rechthoekige driehoek en de hoeken:

• Sinus (sin): sin(hoek) = Overstaande zijde / Schuine zijde
• Cosinus (cos): cos(hoek) = Aanliggende zijde / Schuine zijde
• Tangens (tan): tan(hoek) = Overstaande zijde / Aanliggende zijde

Voorbeeld: Stel dat je een rechthoekige driehoek hebt waarbij de overstaande zijde van hoek A 3 cm is en de schuine zijde 5 cm. Om hoek A te vinden, gebruik je de sinus: sin(A) = 3 / 5 = 0.6. Je neemt de inverse sinus (arcsin) van 0.6 om hoek A te vinden.

Praktische Tips en Voorbeelden

Hier zijn enkele praktische tips om het berekenen van hoeken van driehoeken gemakkelijker te maken:

• Teken een diagram: Visualiseer de driehoek. Dit helpt je om de relaties tussen de zijden en hoeken beter te begrijpen.
• Label de zijden en hoeken duidelijk: Gebruik consistentie in je notatie (bijvoorbeeld, zijde a tegenover hoek A).
• Kies de juiste methode: Denk na over welke informatie je hebt en welke methode het meest geschikt is.
• Controleer je antwoord: Zorg ervoor dat de som van de hoeken in de driehoek 180 graden is.
• Gebruik een rekenmachine: Vooral voor sinus, cosinus, tangens en hun inverse functies.

Voorbeeld 1: Een tuinier wil een bloembed in de vorm van een driehoek maken. Hij weet dat twee van de hoeken 50 graden en 70 graden zijn. Hoeveel graden is de derde hoek? Antwoord: 180 - 50 - 70 = 60 graden.

Voorbeeld 2: Een architect ontwerpt een dak met een helling van 35 graden. De horizontale afstand (aanliggende zijde) is 10 meter. Hij wil weten hoe lang de schuine zijde (de lengte van het dak) moet zijn. Hoewel dit niet direct een hoekberekening is, laat het wel zien hoe trigonometrie gebruikt kan worden. Je kunt de cosinus gebruiken: cos(35) = 10 / schuine zijde. Oplossen voor de schuine zijde geeft: schuine zijde = 10 / cos(35) ≈ 12.21 meter.

Veelgemaakte Fouten en Hoe Ze Te Vermijden

Bij het berekenen van hoeken van driehoeken worden vaak dezelfde fouten gemaakt. Hier zijn enkele veelvoorkomende fouten en hoe je ze kunt vermijden:

• Verkeerde eenheden: Zorg ervoor dat je hoeken in dezelfde eenheden meet (meestal graden).
• Verkeerde formule: Gebruik de juiste formule voor de gegeven informatie. Controleer je formule voordat je begint met rekenen.
• Rekenmachine in de verkeerde modus: Zorg ervoor dat je rekenmachine in de juiste modus staat (graden of radialen).
• Afrondingsfouten: Rond getallen niet te vroeg af tijdens de berekening, anders kan je eindresultaat onnauwkeurig zijn.
• Vergeten de som van de hoeken te controleren: Controleer altijd of de som van de hoeken 180 graden is.

Oefening baart kunst! Hoe meer je oefent met het berekenen van hoeken van driehoeken, hoe beter je er in wordt. Zoek online oefeningen of gebruik een wiskundeboek om je vaardigheden te verbeteren.

Conclusie

Het berekenen van de hoeken van een driehoek is een belangrijke vaardigheid die in veel verschillende situaties van pas kan komen. Door de basisprincipes van driehoeken te begrijpen, de verschillende methoden te kennen en de praktische tips toe te passen, kun je deze vaardigheid onder de knie krijgen. Onthoud de som van de hoeken regel, de sinusregel, de cosinusregel en de specifieke methoden voor rechthoekige driehoeken. En vergeet niet: oefening baart kunst!

Of je nu een student bent die worstelt met geometrie, een doe-het-zelver die een project plant, of gewoon iemand die nieuwsgierig is naar de wereld om je heen, we hopen dat dit artikel je heeft geholpen om de mysteries van driehoeken te ontrafelen. Veel succes met je volgende geometrische uitdaging!