Hoe Bereken Je Het Hellingsgetal

Heb je je ooit afgevraagd hoe steil een berg is waar je tegenop fietst, of hoe veilig een helling is waar je op skiet? Het antwoord schuilt in het hellingsgetal, ook wel de richtingscoëfficiënt genoemd. Het is een simpel getal, maar het vertelt ons veel over de steilheid van een lijn, helling of oppervlakte. Het lijkt misschien wiskundig en ingewikkeld, maar geloof me, het is verrassend toegankelijk. We gaan samen ontdekken hoe je het berekent, en waarom het zo handig is. Ik snap dat wiskunde soms intimiderend kan zijn, maar we gaan het stap voor stap doorlopen.

Waarom is het hellingsgetal belangrijk?

Het hellingsgetal is veel meer dan een abstract concept. Het heeft een directe impact op ons dagelijks leven, en wel op de volgende manieren:

• Veiligheid: Denk aan de bouw van bruggen, wegen en gebouwen. Het hellingsgetal is cruciaal voor het bepalen van de stabiliteit en veiligheid. Een te steile helling kan leiden tot ongelukken.
• Sport en recreatie: Of je nu aan het skiën bent, fietst of wandelt, het hellingsgetal geeft je een idee van de moeilijkheidsgraad en de inspanning die je moet leveren.
• Bouwkunde: Bij het ontwerpen van daken, opritten en tuinen is het hellingsgetal van belang voor de afwatering en de bruikbaarheid van de ruimte.
• Watermanagement: Bij het aanleggen van kanalen en sloten speelt het hellingsgetal een grote rol bij het bepalen van de stroomsnelheid en de afwatering.
• Zonne-energie: De hellingshoek van zonnepanelen is direct van invloed op de efficiëntie van de energieopwekking.

Kortom, het hellingsgetal is overal om ons heen, van de wegen die we berijden tot de huizen waarin we wonen. Het is een fundamenteel concept dat ons helpt de wereld om ons heen beter te begrijpen en veiliger te maken.

Wat is het hellingsgetal precies?

Het hellingsgetal, vaak aangeduid met de letter m, is een maat voor de steilheid van een lijn. Het geeft aan hoeveel de lijn stijgt (of daalt) voor elke eenheid die je naar rechts gaat. Het is de verhouding tussen de verticale verandering (de 'rise') en de horizontale verandering (de 'run').

Denk aan een trap. De helling van de trap is de verhouding tussen de hoogte van elke trede (de rise) en de diepte van elke trede (de run). Een steile trap heeft een grotere rise dan run, en dus een hoger hellingsgetal.

Je kunt het hellingsgetal zien als de 'prijs' die je betaalt in verticale hoogte voor elke stap die je horizontaal zet. Een hoog hellingsgetal betekent dat je veel omhoog gaat voor elke stap naar voren; een laag hellingsgetal betekent dat je bijna plat loopt.

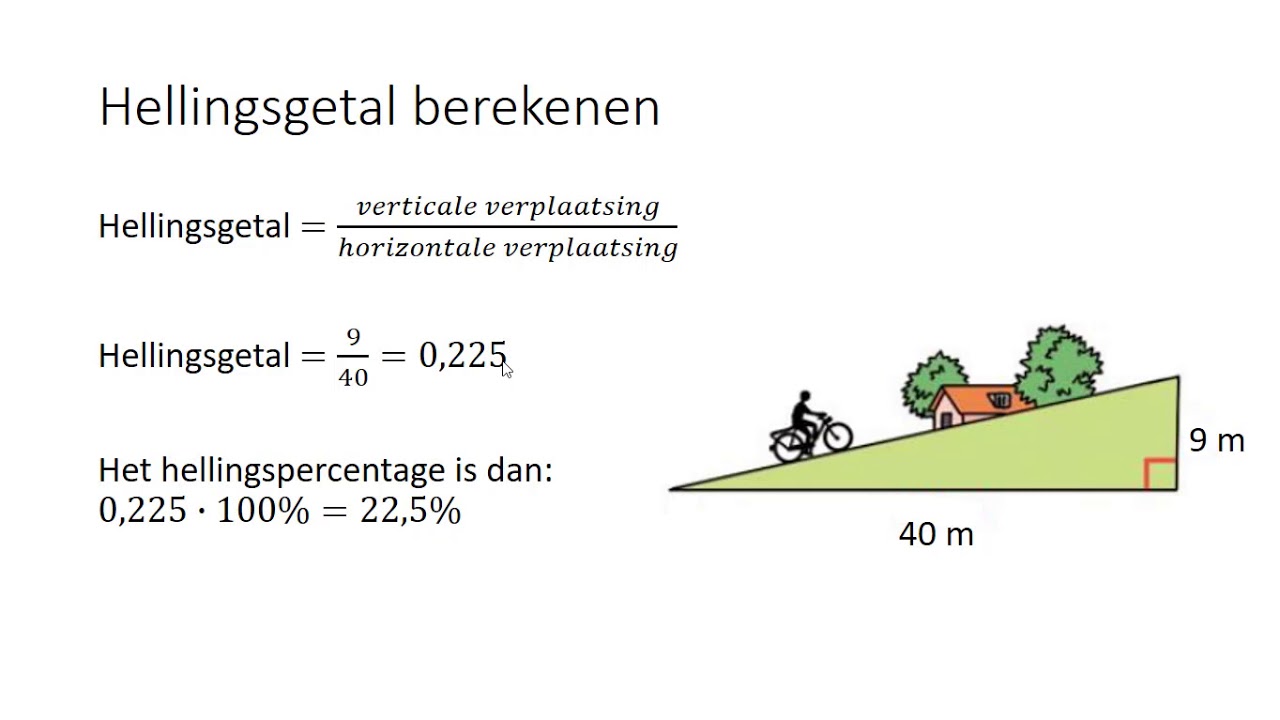
De formule voor het hellingsgetal

De basisformule voor het berekenen van het hellingsgetal is:

m = (y2 - y1) / (x2 - x1)

Waar:

• m het hellingsgetal is
• (x1, y1) de coördinaten zijn van een eerste punt op de lijn
• (x2, y2) de coördinaten zijn van een tweede punt op de lijn

Deze formule geeft je de gemiddelde helling tussen de twee punten. Voor een rechte lijn is de helling overal hetzelfde. Voor een kromme lijn geeft deze formule de helling van de lijn *tussen* de gekozen punten. Om de helling in *een* punt op een kromme lijn te bepalen, heb je differentiaalrekening nodig (maar dat laten we hier buiten beschouwing!).

Hoe bereken je het hellingsgetal? (Stap-voor-stap)

Laten we eens kijken naar een paar praktische voorbeelden om te laten zien hoe eenvoudig het is om het hellingsgetal te berekenen.

Voorbeeld 1:

Stel je voor dat je twee punten op een kaart hebt: A (2, 3) en B (6, 7). Je wilt weten hoe steil de helling is tussen deze twee punten.

1. Identificeer de coördinaten:
   • x1 = 2, y1 = 3
   • x2 = 6, y2 = 7
2. Vul de formule in:
   • m = (7 - 3) / (6 - 2)
3. Bereken:
   • m = 4 / 4 = 1

Dus, het hellingsgetal tussen punt A en punt B is 1. Dit betekent dat voor elke eenheid die je naar rechts gaat, de lijn één eenheid omhoog gaat. Een helling van 1 is dus een hoek van 45 graden.

Voorbeeld 2:

Stel je nu voor dat je een afdaling hebt: C (1, 5) en D (4, 2).

1. Identificeer de coördinaten:
   • x1 = 1, y1 = 5
   • x2 = 4, y2 = 2
2. Vul de formule in:
   • m = (2 - 5) / (4 - 1)
3. Bereken:
   • m = -3 / 3 = -1

In dit geval is het hellingsgetal -1. Het negatieve teken geeft aan dat de lijn daalt in plaats van stijgt. Voor elke eenheid die je naar rechts gaat, daalt de lijn één eenheid.

Speciale gevallen: horizontale en verticale lijnen

Er zijn twee speciale gevallen die je moet onthouden:

• Horizontale lijn: Een horizontale lijn heeft een hellingsgetal van 0. De 'rise' is 0, ongeacht de 'run'. De formule wordt (0 - 0) / (x2 - x1) = 0.
• Verticale lijn: Een verticale lijn heeft een *ongedefinieerd* hellingsgetal. De 'run' is 0, en je kunt niet delen door 0. De formule wordt (y2 - y1) / (0 - 0), wat ongedefinieerd is.

Mogelijke valkuilen en tegenargumenten

Soms kan het berekenen van het hellingsgetal verwarrend zijn, vooral als je met negatieve getallen werkt. Een veelgemaakte fout is het omdraaien van de coördinaten in de formule. Zorg er altijd voor dat je (y2 - y1) deelt door (x2 - x1) en niet andersom. Consistentie is belangrijk: begin met hetzelfde punt in zowel de teller als de noemer.

Sommige mensen beweren dat het hellingsgetal een te simpele weergave is van de werkelijkheid. In complexe situaties, zoals het beoordelen van de veiligheid van een berghelling, zijn er veel meer factoren van belang dan alleen de helling, zoals de samenstelling van de grond, de aanwezigheid van vegetatie en de weersomstandigheden. Dat klopt, maar het hellingsgetal blijft een belangrijke eerste indicator.

Een ander tegenargument is dat de berekening van het hellingsgetal gebaseerd is op een lineair model, terwijl veel hellingen in de praktijk niet lineair zijn. In dergelijke gevallen is het belangrijk om te beseffen dat het berekende hellingsgetal een gemiddelde helling is over het gekozen traject. Voor een nauwkeuriger beeld kan de helling op verschillende punten worden berekend of kunnen meer geavanceerde methoden worden gebruikt.

Tips voor het correct berekenen van het hellingsgetal

Hier zijn nog enkele tips om ervoor te zorgen dat je het hellingsgetal correct berekent:

• Visualiseer: Probeer de lijn of helling visueel voor te stellen. Dit kan je helpen om te bepalen of het hellingsgetal positief of negatief zou moeten zijn.
• Controleer: Controleer je antwoord door de coördinaten in omgekeerde volgorde in te vullen. Het absolute getal moet hetzelfde blijven, alleen het teken kan veranderen (van positief naar negatief of omgekeerd).
• Gebruik een grafiek: Als je moeite hebt met de formule, teken dan de punten op een grafiek en tel het aantal stappen omhoog (of omlaag) en het aantal stappen naar rechts.
• Oefen: Zoals met elke vaardigheid, is oefening belangrijk. Probeer verschillende voorbeelden uit om je vertrouwd te raken met de formule en de verschillende scenario's.

Samenvatting en praktische toepassing

Het hellingsgetal is een krachtig hulpmiddel dat ons helpt de steilheid van lijnen en hellingen te begrijpen. Het is van belang in diverse vakgebieden, van de bouwkunde tot sport en recreatie. Door de formule te begrijpen en de tips te volgen, kun je het hellingsgetal nauwkeurig berekenen en toepassen in verschillende situaties. Onthoud: de formule m = (y2 - y1) / (x2 - x1) is de sleutel!

Denk bijvoorbeeld aan een architect die een oprit voor een rolstoel ontwerpt. De helling mag niet te steil zijn om het voor rolstoelgebruikers makkelijk te maken. Het hellingsgetal helpt de architect om de juiste hoek en lengte te bepalen. Of neem een skiër die een berghelling beoordeelt. De helling geeft een indicatie van de moeilijkheidsgraad van de afdaling.

Tot slot

Nu je weet hoe je het hellingsgetal berekent, waar ga jij het voor gebruiken? Welke helling ga jij analyseren? Kijk eens om je heen en probeer het hellingsgetal te schatten van de hellingen die je ziet. Misschien ontdek je wel nieuwe inzichten over de wereld om je heen!