Hoeveel Diagonalen Heeft Een Vijfhoek

Laten we eerlijk zijn, wiskunde kan soms aanvoelen als een doolhof. Je probeert een probleem op te lossen, en plotseling sta je voor een muur van definities en formules. Vooral meetkunde, met al die hoeken en lijnen, kan best intimiderend zijn. Misschien heb je net een taak gekregen over veelhoeken en je vraagt je af: "Hoeveel diagonalen heeft een vijfhoek eigenlijk?" En eerlijk gezegd, dat is een heel goede vraag!

Geen zorgen, je bent niet alleen! Veel mensen vinden dit soort vragen lastig. Maar het goede nieuws is dat we dit samen stap voor stap kunnen doorlopen. We gaan niet alleen het antwoord geven, maar we gaan je ook laten zien waarom dat het antwoord is, zodat je het begrijpt en het nooit meer vergeet. Dus, laten we die vijfhoek eens nader bekijken en alle diagonalen ontdekken!

Wat is een Diagonaal eigenlijk?

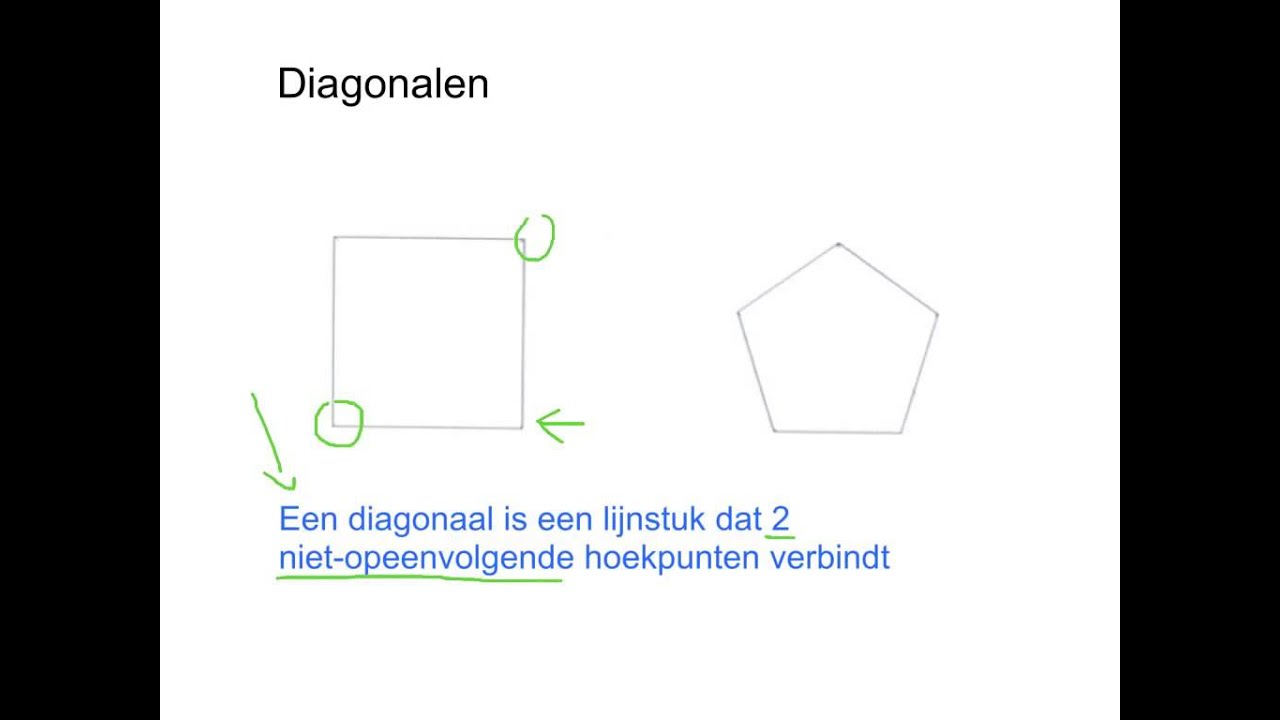
Voordat we ons op de vijfhoek storten, moeten we even stilstaan bij wat een diagonaal precies is. Simpel gezegd, een diagonaal is een lijnstuk dat twee niet-opeenvolgende hoekpunten van een veelhoek verbindt. Niet-opeenvolgende is hier de sleutel. Wat betekent dat?

• Opeenvolgende hoekpunten zijn hoekpunten die direct naast elkaar liggen (zoals de hoeken van een vierkant). Een lijnstuk dat deze verbindt, is een zijde van de veelhoek, geen diagonaal.
• Niet-opeenvolgende hoekpunten zijn hoekpunten die niet direct naast elkaar liggen. De lijnstukken die je hiertussen kunt trekken, noemen we diagonalen.

Stel je een vierkant voor. Twee van de zijden vormen een hoek, maar als je een lijn trekt van de ene hoek naar de hoek tegenover hem, dan heb je een diagonaal gecreëerd. Een vierkant heeft dus twee diagonalen.

Waarom is dit belangrijk?

Je vraagt je misschien af: "Waarom zou ik me hier druk om maken? Wat heb ik aan het aantal diagonalen in een vijfhoek?" Dat is een valide vraag! Maar het concept van diagonalen is eigenlijk best handig, zelfs buiten de schoolbanken. Denk aan:

• Constructie: Ingenieurs gebruiken diagonalen om structuren te verstevigen. Denk aan bruggen of gebouwen. Diagonalen helpen de krachten te verdelen en de structuur stabiel te houden.
• Grafisch ontwerp: Diagonalen kunnen gebruikt worden om dynamiek en visuele interesse toe te voegen aan ontwerpen. Ze leiden het oog en creëren een gevoel van beweging.
• Spelletjes: Denk aan het spel "Vier op een rij". Het concept van diagonalen is essentieel om te begrijpen hoe je kunt winnen!

Dus, hoewel het misschien niet direct duidelijk is, is het begrijpen van diagonalen eigenlijk best handig in verschillende gebieden. Bovendien is het gewoon cool om te weten!

De Vijfhoek: Een Nader Onderzoek

Nu we weten wat een diagonaal is en waarom het belangrijk is, kunnen we ons richten op de vijfhoek. Een vijfhoek is een veelhoek met vijf zijden en vijf hoekpunten. Dat is vrij eenvoudig. Maar hoe zit het met de diagonalen?

Laten we het eens tekenen! Stel je een vijfhoek voor op papier. Kies een hoekpunt. Vanuit dit hoekpunt kun je lijnen trekken naar alle andere hoekpunten. Maar wacht even! Je kunt geen lijn trekken naar het hoekpunt zelf (dat zou geen lijn zijn) en je kunt geen lijnen trekken naar de hoekpunten direct naast dit hoekpunt (dat zouden zijden zijn, geen diagonalen).

Dat betekent dat je vanuit één hoekpunt van een vijfhoek twee diagonalen kunt trekken. Logisch, toch?

De Formule voor Diagonalen

Nu komt het leuke gedeelte. In plaats van te tekenen en te tellen, kunnen we ook een formule gebruiken! De formule om het aantal diagonalen in een veelhoek te berekenen is:

n * (n - 3) / 2

Waar "n" staat voor het aantal zijden (of hoekpunten) van de veelhoek. Klinkt ingewikkeld? Laten we het toepassen op de vijfhoek!

Voor een vijfhoek is n = 5. Dus de formule wordt:

5 * (5 - 3) / 2

Vereenvoudigen we dit:

5 * 2 / 2

10 / 2

5

Dus, een vijfhoek heeft vijf diagonalen! Bingo!

Waarom de Formule Werkt

Misschien vraag je je af: "Waar komt die formule vandaan? Waarom werkt het?" Goede vraag! Hier is een uitleg:

• n * (n - 3): We beginnen met het aantal hoekpunten (n). Van elk hoekpunt kunnen we een lijn trekken naar (n - 3) andere hoekpunten. Waarom -3? Omdat we het hoekpunt zelf en de twee aangrenzende hoekpunten niet meerekenen (want dat zijn geen diagonalen).
• / 2: We delen het resultaat door 2 omdat we anders elke diagonaal twee keer tellen. Stel je voor dat je een diagonaal trekt van hoekpunt A naar hoekpunt C. De formule telt dat als een diagonaal van A naar C, en als een diagonaal van C naar A. Om dit te corrigeren, delen we door 2.

Dus, de formule is eigenlijk een slimme manier om te tellen hoeveel lijnen je kunt trekken, rekening houdend met de regels van diagonalen!

Mogelijke Verwarring en Tegenargumenten

Soms wordt het aantal diagonalen verward met het aantal zijden van een veelhoek. Het is belangrijk te onthouden dat de zijden de lijnen zijn die de opeenvolgende hoekpunten verbinden, terwijl de diagonalen de lijnen zijn die de niet-opeenvolgende hoekpunten verbinden. Ze zijn dus verschillend!

Sommige mensen vinden het misschien makkelijker om simpelweg de diagonalen te tekenen en te tellen. Dat kan zeker werken voor kleinere veelhoeken zoals de vijfhoek. Maar voor grotere veelhoeken, zoals een tienhoek of een twaalfhoek, wordt het al snel erg onoverzichtelijk en is de formule veel efficiënter.

Samenvatting en Praktische Toepassing

Laten we alles nog eens samenvatten:

• Een diagonaal is een lijnstuk dat twee niet-opeenvolgende hoekpunten van een veelhoek verbindt.
• Een vijfhoek is een veelhoek met vijf zijden en vijf hoekpunten.
• De formule voor het berekenen van het aantal diagonalen in een veelhoek is: n * (n - 3) / 2
• Een vijfhoek heeft vijf diagonalen.

Je kunt deze kennis nu gebruiken om het aantal diagonalen van andere veelhoeken te berekenen. Probeer het eens met een zeshoek (n = 6) of een achthoek (n = 8)!

Verder Kijken: Diagonalen in de Hogere Wiskunde

Hoewel we ons nu op basisch meetkundig niveau bevinden, is het goed om te weten dat het concept van diagonalen ook in de hogere wiskunde voorkomt. In de lineaire algebra, bijvoorbeeld, wordt de term "diagonaliseren" gebruikt om een matrix te vereenvoudigen door deze om te zetten in een diagonaalmatrix. Dit heeft belangrijke toepassingen in onder andere de quantummechanica en de systeemtheorie.

Het is dus fascinerend om te zien hoe iets wat begint als een simpele vraag over een vijfhoek, eigenlijk de opstap kan zijn naar complexere en diepgaandere wiskundige concepten!

Conclusie

Hopelijk heb je nu een beter begrip van wat diagonalen zijn en hoe je het aantal diagonalen in een vijfhoek (en andere veelhoeken) kunt berekenen. Wiskunde hoeft geen angstaanjagend doolhof te zijn. Door de concepten stap voor stap te doorlopen en de waarom te begrijpen, kan het juist leuk en bevredigend zijn.

Dus, voel je je nu zekerder over meetkunde? Wat ga je nu berekenen?