Wat Is Een Wetenschappelijke Notatie
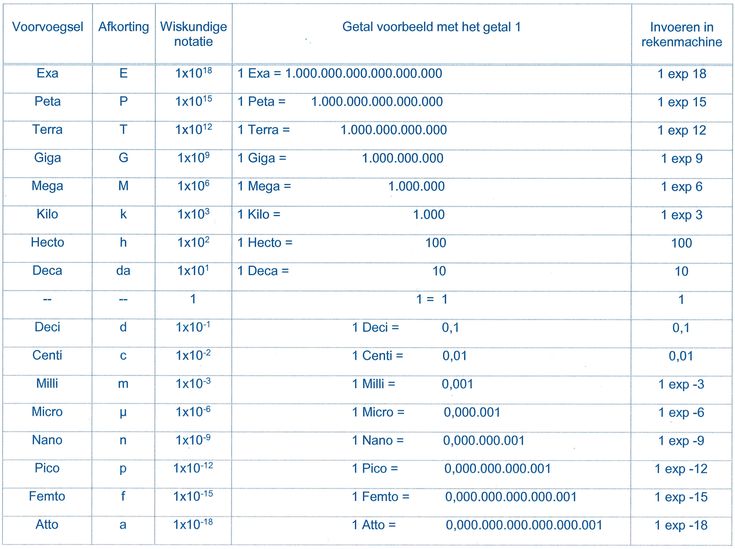
Wetenschappelijke notatie, ook wel exponentiële notatie genoemd, is een manier om zeer grote of zeer kleine getallen op een compacte en handige manier weer te geven. In plaats van lange reeksen nullen te schrijven, gebruiken we machten van tien om de orde van grootte aan te geven. Dit maakt berekeningen en vergelijkingen een stuk overzichtelijker, vooral in vakgebieden zoals wetenschap, techniek en wiskunde.
De Basis van Wetenschappelijke Notatie
De algemene vorm van een getal in wetenschappelijke notatie is a × 10b, waarbij:
- a de mantisse of significant wordt genoemd. Dit is een reëel getal tussen 1 (inclusief) en 10 (exclusief).
- 10 is het grondtal. In dit geval gebruiken we het decimale stelsel (basis 10).
- b is de exponent. Dit is een geheel getal dat aangeeft hoeveel plaatsen de komma in de mantisse verschoven moet worden om het oorspronkelijke getal te verkrijgen.
Bijvoorbeeld, het getal 300.000.000 (300 miljoen) kan in wetenschappelijke notatie geschreven worden als 3 × 108. Het getal 0,000000005 (5 miljardste) kan geschreven worden als 5 × 10-9. Je ziet direct dat dit een stuk compacter is.
Positieve Exponenten
Een positieve exponent geeft aan dat het getal groter is dan 1. De exponent vertelt je hoeveel plaatsen je de komma naar rechts moet verschuiven in de mantisse om het oorspronkelijke getal te krijgen. Denk aan het voorbeeld van 3 × 108. De komma in de 3 (die eigenlijk 3,0 is) moet 8 plaatsen naar rechts verschoven worden. Omdat we geen andere cijfers hebben dan de 3, vullen we aan met nullen: 300.000.000.
Negatieve Exponenten
Een negatieve exponent geeft aan dat het getal kleiner is dan 1. De exponent (zonder het minteken) vertelt je hoeveel plaatsen je de komma naar links moet verschuiven in de mantisse om het oorspronkelijke getal te krijgen. In het voorbeeld 5 × 10-9 moet de komma in de 5 (eigenlijk 5,0) 9 plaatsen naar links verschoven worden. Ook hier vullen we aan met nullen: 0,000000005.
Waarom Wetenschappelijke Notatie Gebruiken?
Er zijn verschillende redenen waarom wetenschappelijke notatie zo nuttig is:
- Compactheid: Zoals eerder genoemd, maakt het enorm grote en kleine getallen veel korter en overzichtelijker.
- Leesbaarheid: Het is makkelijker om de orde van grootte van een getal in wetenschappelijke notatie te zien, wat het vergelijken van getallen eenvoudiger maakt.
- Nauwkeurigheid: Wetenschappelijke notatie helpt bij het weergeven van significante cijfers, wat cruciaal is voor de nauwkeurigheid van metingen en berekeningen.
- Voorkomen van Fouten: Het vermindert de kans op fouten bij het tellen van nullen in lange getallen.
Rekenen met Wetenschappelijke Notatie
Het rekenen met getallen in wetenschappelijke notatie is relatief eenvoudig, zolang je de regels goed volgt.
Vermenigvuldigen
Om twee getallen in wetenschappelijke notatie te vermenigvuldigen, vermenigvuldig je de mantisses en tel je de exponenten op:
(a × 10b) × (c × 10d) = (a × c) × 10(b + d)
Voorbeeld: (2 × 103) × (3 × 104) = (2 × 3) × 10(3 + 4) = 6 × 107
Delen
Om twee getallen in wetenschappelijke notatie te delen, deel je de mantisses en trek je de exponenten af:
(a × 10b) / (c × 10d) = (a / c) × 10(b - d)
Voorbeeld: (8 × 106) / (2 × 102) = (8 / 2) × 10(6 - 2) = 4 × 104
Optellen en Aftrekken
Om twee getallen in wetenschappelijke notatie op te tellen of af te trekken, moeten ze dezelfde exponent hebben. Zo niet, dan moet je één van de getallen aanpassen om dit te bereiken.
Zodra de exponenten gelijk zijn, kun je de mantisses optellen of aftrekken en de exponent behouden:
(a × 10b) + (c × 10b) = (a + c) × 10b
(a × 10b) - (c × 10b) = (a - c) × 10b
Voorbeeld: (5 × 104) + (3 × 104) = (5 + 3) × 104 = 8 × 104
Voorbeeld (met aanpassing): (5 × 104) + (3 × 103) = (5 × 104) + (0,3 × 104) = (5 + 0,3) × 104 = 5,3 × 104
Real-World Voorbeelden en Data
Wetenschappelijke notatie wordt in veel verschillende contexten gebruikt.
- Astronomie: De afstand tussen de aarde en de zon is ongeveer 1,496 × 1011 meter. De massa van de zon is ongeveer 1,989 × 1030 kg.
- Chemie: De constante van Avogadro (het aantal atomen of moleculen in een mol) is ongeveer 6,022 × 1023.
- Informatica: De opslagcapaciteit van een harde schijf kan worden uitgedrukt in bytes, bijvoorbeeld 1 × 1012 bytes (1 terabyte).
- Natuurkunde: De lichtsnelheid in vacuüm is ongeveer 3 × 108 meter per seconde. De constante van Planck is ongeveer 6,626 × 10-34 joule-seconde.
- Biologie: De geschatte aantal bacteriën op aarde is 5 × 1030.
Deze voorbeelden illustreren hoe essentieel wetenschappelijke notatie is voor het werken met getallen die anders onpraktisch lang zouden zijn.
Rekenmachines en Computers
De meeste rekenmachines en computerprogramma's ondersteunen wetenschappelijke notatie. Ze gebruiken vaak een 'E' of 'e' om de macht van 10 aan te duiden. Bijvoorbeeld, 3 × 108 zou op een rekenmachine weergegeven kunnen worden als 3E8 of 3e8. Het is belangrijk om te weten hoe je rekenmachine wetenschappelijke notatie weergeeft, zodat je de resultaten correct kunt interpreteren.
Significante Cijfers en Wetenschappelijke Notatie
Wetenschappelijke notatie is ook handig voor het weergeven van het juiste aantal significante cijfers. Significante cijfers zijn de cijfers in een getal die een betekenis hebben voor de nauwkeurigheid van de meting. Door het getal in wetenschappelijke notatie te zetten, kun je duidelijk aangeven welke cijfers significant zijn.
Bijvoorbeeld, als je een meting hebt van 1200 meter en je weet dat de meting nauwkeurig is tot op de honderdtallen, dan heeft het getal twee significante cijfers. Je kunt dit weergeven als 1,2 × 103 meter. Als je de meting nauwkeurig tot op de eenheden zou weten, zou je het schrijven als 1,200 × 103 meter (vier significante cijfers).
Conclusie
Wetenschappelijke notatie is een krachtig hulpmiddel voor het weergeven en manipuleren van zeer grote en zeer kleine getallen. Het is essentieel in vele wetenschappelijke en technische disciplines, en het helpt om berekeningen te vereenvoudigen, fouten te voorkomen en de nauwkeurigheid te waarborgen. Door de basisprincipes van wetenschappelijke notatie te begrijpen, ben je beter in staat om complexe gegevens te interpreteren en te verwerken.
Oefen met het omzetten van getallen naar en van wetenschappelijke notatie, en gebruik het in je eigen berekeningen. Hoe meer je ermee werkt, hoe vertrouwder je ermee zult raken, en hoe meer je de voordelen ervan zult inzien. Of je nu bezig bent met astronomie, chemie, informatica of een ander vakgebied, wetenschappelijke notatie zal je helpen om efficiënter en nauwkeuriger te werken!

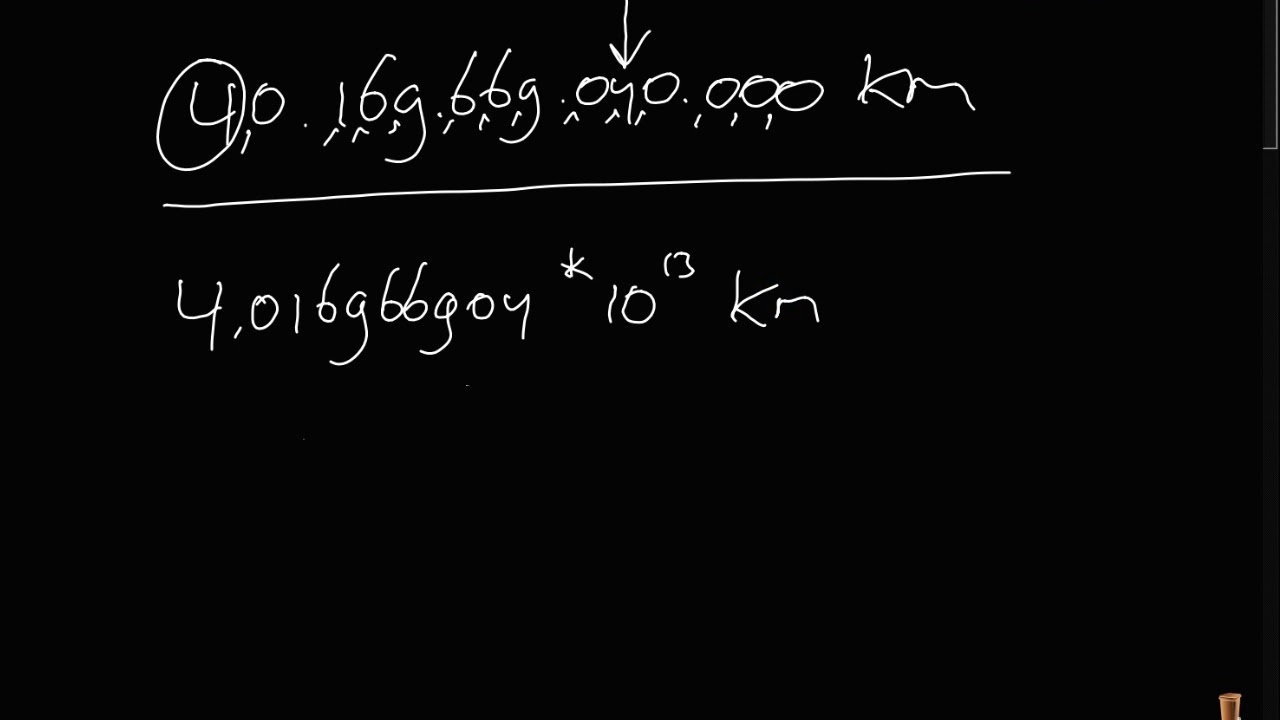
Bekijk ook deze gerelateerde berichten:
- Ger Gem In Ned Goes
- Verschil Pet Scan En Ct Scan
- Wie Was In 1953 De Opvolger Van Stalin
- Hoe Bereken Je 21 Van Een Bedrag
- Hoe Bereken Je Het Hellingsgetal
- Ruud En Corry Van Veen
- Kindergebedjes Voor Het Slapen Gaan
- Wat Is Een Mediaan Wiskunde
- Wat Is De Functie Van De Gal
- Hoe Bereken Je De Current Ratio
