Breuken Omzetten Naar Kommagetallen Werkblad

We kennen het allemaal: die momenten in de wiskundeles waarop breuken plotseling op ons afkomen als een ondoordringbare muur. Je kijkt naar die ¹/₂, ³/₄ of zelfs complexere varianten, en je vraagt je af: "Hoe kan ik dit in vredesnaam omzetten naar een kommagetal?" Het is frustrerend, je voelt je misschien dom, en je vraagt je af wanneer je dit ooit in het echte leven nodig zult hebben. Gelukkig ben je niet alleen, en het is zeker niet zo ingewikkeld als het lijkt.

Dit artikel is speciaal geschreven voor jou: de leerling die worstelt met het omzetten van breuken naar kommagetallen. We begrijpen je uitdagingen, en we gaan je stap voor stap laten zien hoe je dit onder de knie kunt krijgen. Bovendien laten we je zien waarom dit *belangrijk* is, verder dan alleen maar het halen van een goed cijfer.

Waarom zou je breuken naar kommagetallen willen omzetten?

Op het eerste gezicht lijkt het misschien een abstracte wiskundige oefening, maar het omzetten van breuken naar kommagetallen heeft talloze praktische toepassingen in het dagelijks leven:

• Koken en bakken: Recepten gebruiken vaak breuken (¹/₃ kop, ¹/₄ theelepel). Een kommagetal (0,33 kop, 0,25 theelepel) kan het makkelijker maken om de juiste hoeveelheid af te meten, vooral als je een digitale weegschaal gebruikt.
• Winkelen: Kortingen worden vaak als percentages (een vorm van kommagetallen) weergegeven, maar de originele prijs kan je misschien in een breuk noteren (¹/₂ van de prijs). Het omzetten helpt je snel de uiteindelijke prijs te berekenen.
• Metingen en constructie: Bij het bouwen of klussen kom je vaak breuken tegen bij het meten van materialen. Omzetten naar kommagetallen kan het snijden en aanpassen preciezer maken. Denk aan een plank die ⁵/₈ inch dik is.
• Financiën: Rentepercentages en aandelenprijzen worden vaak als kommagetallen weergegeven. Inzicht in hoe breuken en kommagetallen zich tot elkaar verhouden, helpt je betere financiële beslissingen te nemen.
• Sport: Kijk maar naar honkbal! De batting average van een speler wordt uitgedrukt in een kommagetal, wat in feite een breuk is van het aantal hits gedeeld door het aantal at bats.

Zoals je ziet, is het omzetten van breuken naar kommagetallen niet alleen nuttig voor wiskundetoetsen, maar ook voor allerlei situaties in het echte leven. Het geeft je een beter gevoel voor getallen en helpt je problemen op te lossen.

Hoe zet je een breuk om naar een kommagetal?

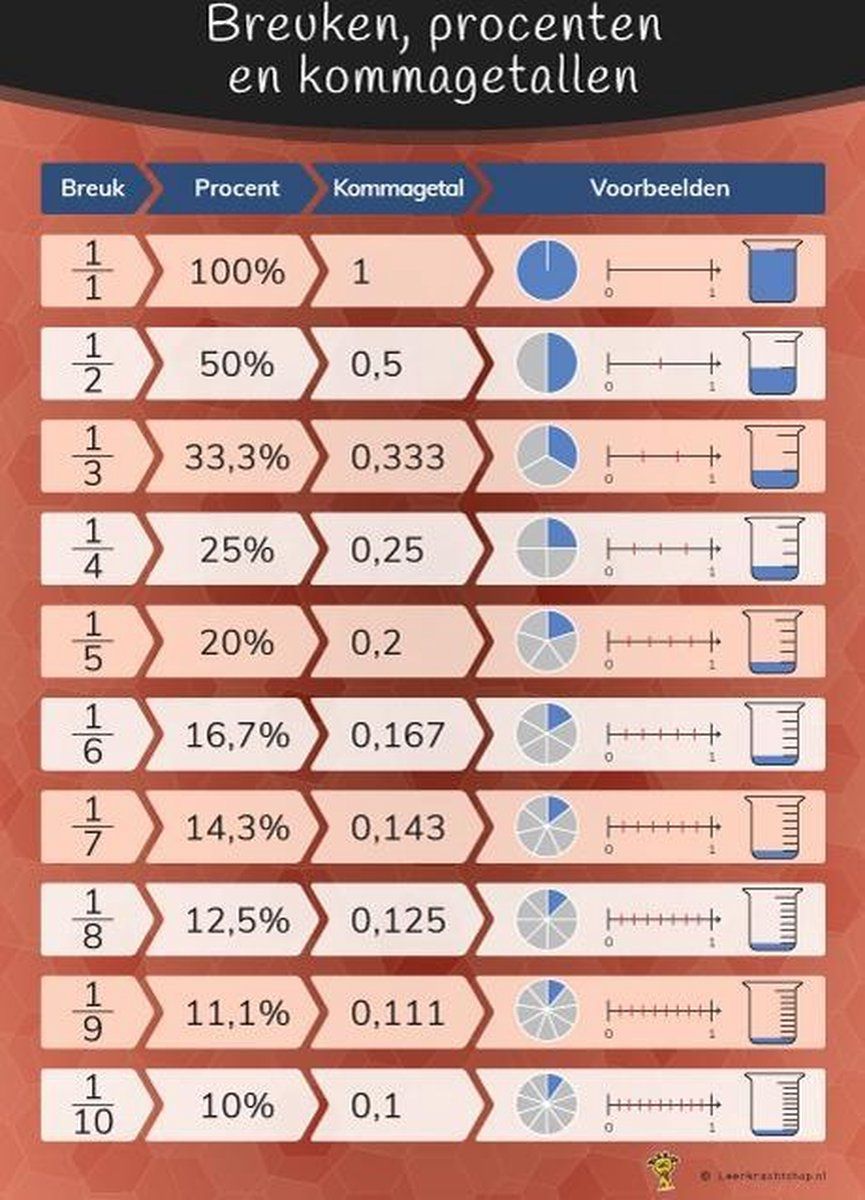
De basisregel is simpel: Deel de teller door de noemer. Dat is alles! Laten we een paar voorbeelden bekijken:

Eenvoudige voorbeelden:

• ¹/₂: Deel 1 door 2 = 0,5
• ¹/₄: Deel 1 door 4 = 0,25
• ³/₄: Deel 3 door 4 = 0,75

In deze voorbeelden krijg je een eindig kommagetal. Dat betekent dat de deling "netjes" uitkomt en je geen oneindige reeks cijfers achter de komma hebt.

Lastigere voorbeelden:

Sommige breuken leveren oneindige kommagetallen op. Dit betekent dat de deling nooit helemaal "uitkomt" en je een zich herhalend patroon van cijfers achter de komma krijgt.

• ¹/₃: Deel 1 door 3 = 0,3333... (het cijfer 3 herhaalt zich oneindig)
• ²/₃: Deel 2 door 3 = 0,6666... (het cijfer 6 herhaalt zich oneindig)

We schrijven deze oneindige kommagetallen vaak afgerond, of met een streep boven het herhalende cijfer (bijvoorbeeld 0,3). In veel gevallen is het voldoende om de eerste paar decimalen te berekenen en af te ronden.

Gemengde getallen:

Een gemengd getal bestaat uit een heel getal en een breuk (bijvoorbeeld 2 ¹/₂). Om dit om te zetten naar een kommagetal, kun je twee dingen doen:

1. Zet de breuk om naar een kommagetal en tel dit op bij het hele getal. In het voorbeeld: ¹/₂ = 0,5. Dus 2 ¹/₂ = 2 + 0,5 = 2,5
2. Zet het gemengde getal eerst om naar een onechte breuk. In het voorbeeld: 2 ¹/₂ = ⁵/₂. Deel vervolgens de teller door de noemer: 5 / 2 = 2,5

Beide methoden werken, kies degene die je het prettigst vindt!

Handige hulpmiddelen

Je hoeft het niet allemaal uit je hoofd te leren. Er zijn veel handige hulpmiddelen die je kunt gebruiken:

• Rekenmachine: De meest voor de hand liggende optie. Je kunt eenvoudig de teller delen door de noemer.
• Online breuk-naar-kommagetal converters: Er zijn talloze websites die deze conversie voor je doen. Voer de breuk in en de converter geeft je het equivalente kommagetal.
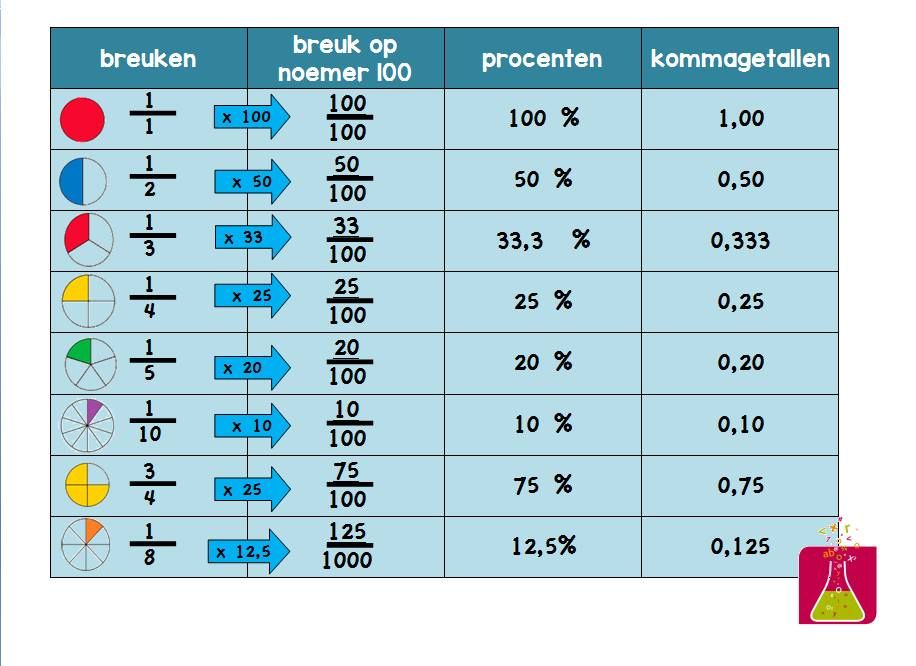
• Breukentabel: Een tabel met veel voorkomende breuken en hun decimale equivalenten. Dit kan handig zijn om snel antwoorden te vinden.
• Apps voor wiskunde: Er zijn apps die je stap voor stap laten zien hoe je breuken omzet naar kommagetallen, en je oefeningen geven om te oefenen.

Veelgemaakte fouten en hoe je ze kunt vermijden

Zelfs met de juiste kennis, kunnen er fouten insluipen. Hier zijn een paar veelgemaakte fouten en hoe je ze kunt vermijden:

• De teller en noemer verwisselen: Zorg ervoor dat je *altijd* de teller deelt door de noemer. Dit is een veelgemaakte beginnersfout.
• Verkeerd afronden: Let op de afrondingsregels. Als het cijfer na de laatste decimaal die je wilt behouden 5 of hoger is, rond je omhoog.
• Tekens vergeten: Als de breuk negatief is, moet het kommagetal ook negatief zijn.
• De herhaling negeren: Bij oneindige kommagetallen is het belangrijk om de herhaling te herkennen en correct weer te geven (bijvoorbeeld met een streep boven het herhalende cijfer).

Counterpoints: Waarom zou je *niet* breuken naar kommagetallen omzetten?

Hoewel het omzetten van breuken naar kommagetallen in veel situaties handig is, zijn er ook momenten waarop het beter is om de breuk te laten staan. Soms is de breuk zelf nauwkeuriger dan het afgeronde kommagetal. Bijvoorbeeld, als je een exacte waarde nodig hebt voor een complexe berekening, kan het werken met de breuk nauwkeuriger zijn. In sommige wetenschappelijke of technische contexten is het behouden van de breuk de voorkeur.

Het is dus belangrijk om te begrijpen wanneer het omzetten nuttig is, en wanneer het beter is om met breuken te blijven werken. Het is geen kwestie van "of/of", maar van "wanneer".

Oefenen, oefenen, oefenen!

Net als bij elke vaardigheid, geldt ook hier: oefening baart kunst. Download een werkblad met breuken om om te zetten naar kommagetallen. Zoek online naar oefeningen, of maak je eigen. Hoe meer je oefent, hoe sneller en nauwkeuriger je zult worden.

Voorbeelden van oefeningen op een werkblad:

1. Zet de volgende breuken om naar kommagetallen: ²/₅, ⁷/₈, ¹/₁₀, ⁵/₆, ¹¹/₂₀
2. Zet de volgende gemengde getallen om naar kommagetallen: 1 ¹/₄, 3 ¹/₂, 5 ³/₈, 2 ²/₃
3. Los de volgende problemen op:
   • Je hebt ³/₄ van een pizza gegeten. Hoeveel is dat als kommagetal?
   • Een korting van ¹/₃ op een product van €15. Wat is de nieuwe prijs in decimalen afgerond?

Conclusie

Het omzetten van breuken naar kommagetallen is een waardevolle vaardigheid die je op allerlei manieren kan helpen, zowel op school als in het dagelijks leven. Hoewel het in het begin misschien lastig lijkt, is het met de juiste uitleg en oefening zeker te leren. Blijf oefenen, gebruik de beschikbare hulpmiddelen, en wees niet bang om fouten te maken. Van fouten leer je immers!

Nu je meer weet over het omzetten van breuken naar kommagetallen, welke breuk ga jij als eerste omzetten, en waar ga je deze kennis toepassen?