Dy Dx Op Grafische Rekenmachine

De grafische rekenmachine is een onmisbaar hulpmiddel geworden voor studenten en professionals in diverse vakgebieden, van wiskunde en natuurkunde tot economie en engineering. Eén van de krachtigste functies, met name voor studenten die calculus leren, is de mogelijkheid om afgeleiden (dy/dx) te berekenen en grafisch weer te geven. Dit artikel duikt diep in de wereld van dy/dx op de grafische rekenmachine, bespreekt de belangrijkste concepten, voordelen en praktische toepassingen, en biedt een overzicht van hoe deze functie je kan helpen bij het oplossen van complexe problemen.

De Basis van Afgeleiden (dy/dx)

Voordat we dieper ingaan op de functionaliteit van de grafische rekenmachine, is het belangrijk om de fundamentele concepten van afgeleiden te begrijpen. In de wiskunde, en specifiek in de calculus, vertegenwoordigt de afgeleide van een functie y = f(x) de momentane veranderingssnelheid van y met betrekking tot x. Anders gezegd, het is de helling van de raaklijn aan de grafiek van de functie op een bepaald punt.

De notatie dy/dx (uitgesproken als "dee y dee x") is de meest voorkomende manier om een afgeleide aan te duiden. De 'd' staat voor 'differentieel', wat een infinitesimale verandering in de respectievelijke variabele vertegenwoordigt.

Wat betekent dit concreet? Stel je een auto voor die rijdt. De functie y = f(x) kan de afgelegde afstand (y) voorstellen als functie van de tijd (x). De afgeleide dy/dx op een bepaald tijdstip (x) is dan de snelheid van de auto op dat moment. Een positieve dy/dx betekent dat de afstand toeneemt (de auto rijdt vooruit), een negatieve dy/dx betekent dat de afstand afneemt (de auto rijdt achteruit), en dy/dx = 0 betekent dat de auto stilstaat.

Waarom zijn afgeleiden belangrijk?

Afgeleiden zijn essentieel in vele wetenschappelijke en technische disciplines omdat ze gebruikt kunnen worden om:

Optimalisatieproblemen op te lossen: Het vinden van maxima en minima van functies (bijvoorbeeld het maximaliseren van winst of het minimaliseren van kosten).
Veranderingsprocessen te modelleren: Het beschrijven van hoe grootheden in de loop van de tijd veranderen (bijvoorbeeld de groeisnelheid van een populatie of de snelheid van een chemische reactie).
Fysische systemen te analyseren: Het bestuderen van beweging, krachten en energie (bijvoorbeeld de versnelling van een object onder invloed van zwaartekracht).

De Grafische Rekenmachine als Hulpmiddel voor Afgeleiden

De grafische rekenmachine biedt krachtige tools om afgeleiden te berekenen, grafisch weer te geven en te analyseren. Dit kan een aanzienlijke tijdswinst opleveren en het begrip van de onderliggende concepten verdiepen.

Numerieke Differentiatie

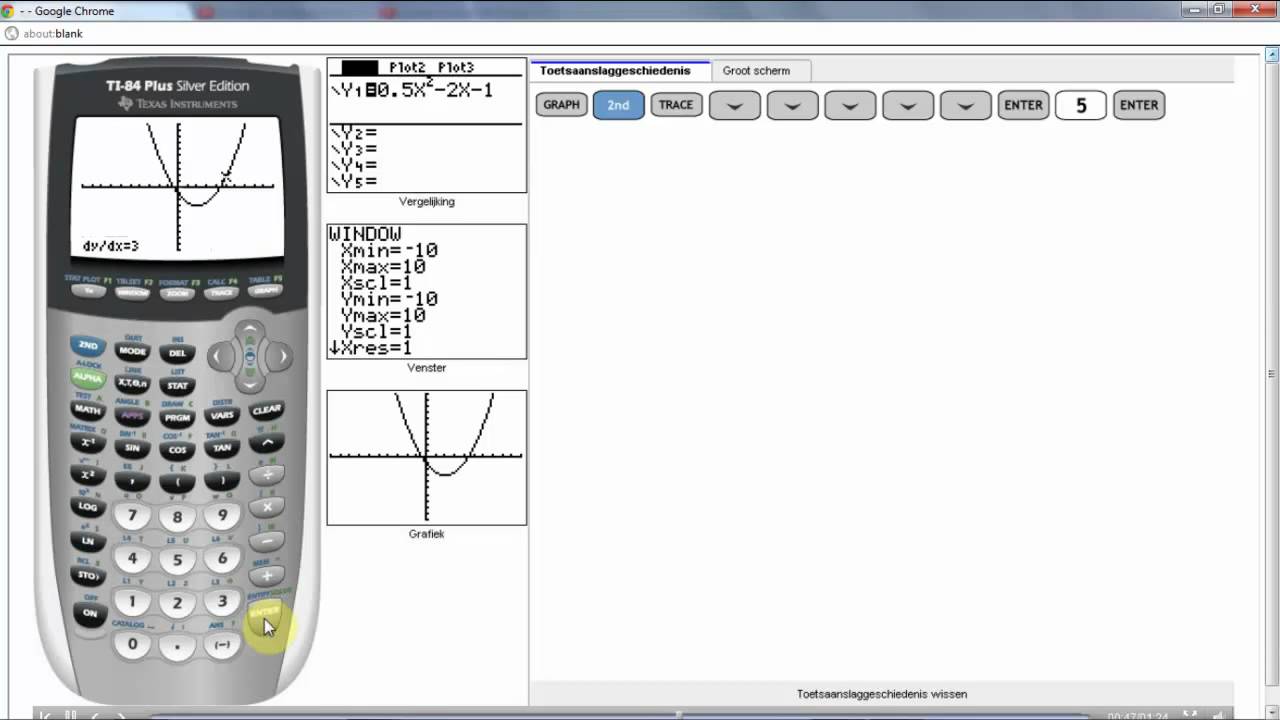
De meeste grafische rekenmachines hebben een ingebouwde functie voor numerieke differentiatie. Dit betekent dat de rekenmachine de afgeleide van een functie op een specifiek punt kan benaderen met behulp van numerieke methoden. Je voert de functie, de variabele waarnaar je differentieert (x), en de waarde van x in, en de rekenmachine geeft een benadering van dy/dx op dat punt. Dit is vooral handig voor functies die moeilijk of onmogelijk analytisch (met de hand) te differentiëren zijn.

Voorbeeld: Stel dat je de afgeleide van f(x) = x³ + 2x² - 5x + 1 wilt berekenen op x = 2. Op de meeste rekenmachines kun je dit invoeren als nDeriv(x³ + 2x² - 5x + 1, x, 2). De rekenmachine zal een waarde geven die dicht bij de werkelijke afgeleide ligt (in dit geval 11).

Grafische Weergave van Afgeleiden

Een van de meest waardevolle mogelijkheden van de grafische rekenmachine is de mogelijkheid om de afgeleide functie te plotten. Dit geeft je een visueel inzicht in hoe de veranderingssnelheid van de oorspronkelijke functie varieert over een bepaald interval. Je kunt de grafiek van de functie f(x) plotten en tegelijkertijd de grafiek van zijn afgeleide f'(x) (of dy/dx). Door beide grafieken te vergelijken, kun je relaties tussen de functie en zijn afgeleide observeren, zoals:

Waar de functie stijgt of daalt: Als de afgeleide positief is, stijgt de functie; als de afgeleide negatief is, daalt de functie.
Waar de functie een maximum of minimum heeft: Maxima en minima van de functie komen overeen met punten waar de afgeleide nul is (kritieke punten).
Waar de functie concaaf omhoog of omlaag is: De tweede afgeleide (de afgeleide van de afgeleide) geeft informatie over de concaafheid van de functie.

Voorbeeld: Plot de functie f(x) = sin(x). Je zult zien dat de afgeleide (dy/dx = cos(x)) positief is wanneer sin(x) stijgt, negatief wanneer sin(x) daalt, en nul bij de maxima en minima van sin(x).

Het Berekenen van Raaklijnen

Grafische rekenmachines kunnen ook de vergelijking van de raaklijn aan een functie op een specifiek punt berekenen en plotten. Dit is een visuele representatie van de afgeleide op dat punt. De raaklijn is een rechte lijn die de grafiek van de functie op dat punt raakt en dezelfde helling heeft als de afgeleide op dat punt.

Hoe werkt dit? Je kiest een punt op de grafiek (bijvoorbeeld x = a). De rekenmachine berekent de waarde van de functie (f(a)) en de afgeleide (f'(a)) op dat punt. Vervolgens gebruikt hij de punt-helling vorm van een rechte lijn (y - f(a) = f'(a)(x - a)) om de vergelijking van de raaklijn te bepalen. De rekenmachine kan deze lijn vervolgens grafisch weergeven, waardoor je een directe visualisatie hebt van de afgeleide als helling van de raaklijn.

Praktische Toepassingen en Voorbeelden

De mogelijkheid om dy/dx te berekenen en te visualiseren op een grafische rekenmachine is nuttig in verschillende contexten:

Natuurkunde: Het bepalen van de snelheid en versnelling van een object, gegeven de positie als functie van de tijd. Stel je voor dat je de positie van een projectiel hebt beschreven als y(t). De afgeleide dy/dt is dan de snelheid van het projectiel op tijdstip t, en de tweede afgeleide (de afgeleide van de snelheid) is de versnelling.
Economie: Het analyseren van marginale kosten en opbrengsten. Als C(x) de kosten voorstelt om x eenheden van een product te produceren, dan is dC/dx de marginale kost, de geschatte kosten om één extra eenheid te produceren.
Biologie: Het modelleren van de groeisnelheid van een populatie. Als P(t) de populatie op tijdstip t voorstelt, dan is dP/dt de groeisnelheid van de populatie.
Engineering: Het optimaliseren van ontwerpen en processen. Bijvoorbeeld, het vinden van de afmetingen van een container die het maximale volume kan bevatten bij een gegeven hoeveelheid materiaal.

Een concreet voorbeeld: Een bedrijf wil de winst maximaliseren door de prijs van een product aan te passen. De winst P kan worden uitgedrukt als functie van de prijs x: P(x) = x * D(x) - C(x), waarbij D(x) de vraag is als functie van de prijs en C(x) de kosten. Om de winst te maximaliseren, berekent het bedrijf dP/dx en stelt het gelijk aan nul. De grafische rekenmachine kan helpen bij het plotten van P(x) en dP/dx om de optimale prijs te vinden waar dP/dx = 0, wat overeenkomt met een maximum van de winst.

Tips en Trucs voor het Gebruik van dy/dx op een Grafische Rekenmachine

Hier zijn enkele tips om het meeste uit de dy/dx functionaliteit van je grafische rekenmachine te halen:

Ken je rekenmachine: Lees de handleiding van je rekenmachine om te leren hoe je de nDeriv functie, de grafische functies en de raaklijn functie correct gebruikt. De exacte syntax kan verschillen per model.
Wees nauwkeurig met je input: Zorg ervoor dat je de functie correct invoert en dat je de juiste variabele en punt specificeert. Typfouten kunnen leiden tot onjuiste resultaten.
Experimenteer met de window instellingen: Pas de X-min, X-max, Y-min en Y-max waarden aan om de grafieken duidelijk weer te geven. Soms moet je in- of uitzoomen om de interessante kenmerken van de grafiek te zien.
Gebruik de trace functie: De trace functie kan worden gebruikt om de coördinaten van punten op de grafiek te bepalen, inclusief de waarden van de afgeleide.
Controleer je antwoorden: Verifieer je resultaten indien mogelijk met behulp van andere methoden, zoals analytische berekeningen of online calculators.

Conclusie

De mogelijkheid om dy/dx (afgeleiden) te berekenen en grafisch weer te geven op een grafische rekenmachine is een ongelooflijk krachtig hulpmiddel voor het begrijpen en toepassen van calculusconcepten. Het stelt je in staat om veranderingsprocessen te visualiseren, optimalisatieproblemen op te lossen en complexe modellen te analyseren. Door de functionaliteit van je rekenmachine te leren kennen en te oefenen met verschillende voorbeelden, kun je je vaardigheden in calculus aanzienlijk verbeteren en je succes in wiskunde, wetenschap en engineering vergroten.

Aanmoediging: Pak je grafische rekenmachine, kies een paar functies uit je calculusboek, en begin te experimenteren met het berekenen en plotten van afgeleiden. Hoe meer je oefent, hoe comfortabeler je zult worden met het gebruik van dit waardevolle hulpmiddel en hoe beter je de onderliggende concepten zult begrijpen.