Fixed Effect Or Random Effect

We begrijpen het: statistiek kan intimiderend zijn. Vooral als je voor de keuze staat tussen fixed effects en random effects modellen. Het voelt alsof je navigeert door een doolhof vol formules en jargon. Maar vrees niet! Dit artikel is er om je te helpen. We gaan deze concepten ontrafelen, niet door abstracte theorieën te spuien, maar door te laten zien hoe ze jouw onderzoek of analyse in de praktijk beïnvloeden.

De Impact in de Werkelijkheid

Stel je voor: je bent een onderzoeker die de effectiviteit van verschillende lesmethoden op de schoolprestaties van leerlingen wil onderzoeken. Je verzamelt data van leerlingen in verschillende scholen. De keuze tussen een fixed effects en een random effects model is dan cruciaal. Het bepaalt niet alleen de resultaten van je analyse, maar ook de interpreteerbaarheid en generaliseerbaarheid van je bevindingen. Een verkeerde keuze kan leiden tot misleidende conclusies, wat weer invloed kan hebben op het onderwijsbeleid!

Of neem een marketeer die de effectiviteit van verschillende marketingcampagnes in verschillende regio's wil meten. Fixed effects en random effects modellen kunnen helpen om de specifieke effecten van elke campagne te isoleren en tegelijkertijd rekening te houden met de verschillen tussen de regio's. Dit is essentieel om je marketingbudget effectief te alloceren.

Wat zijn Fixed Effects en Random Effects eigenlijk?

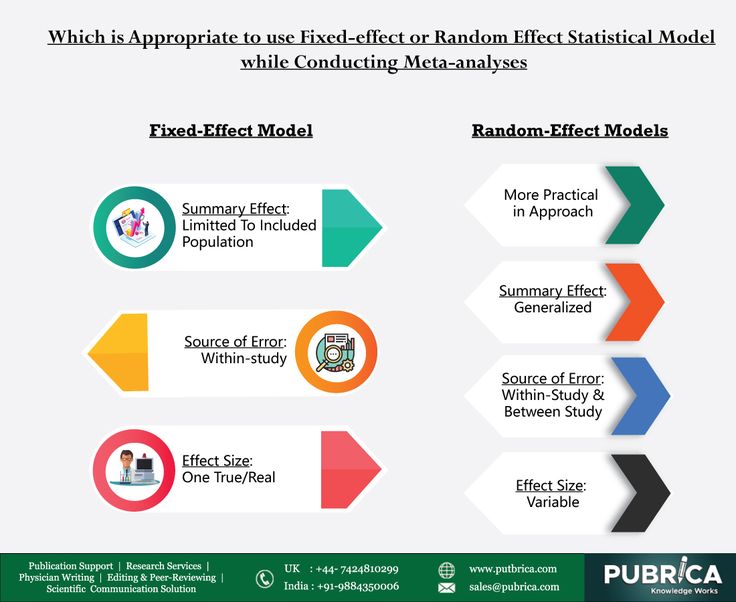
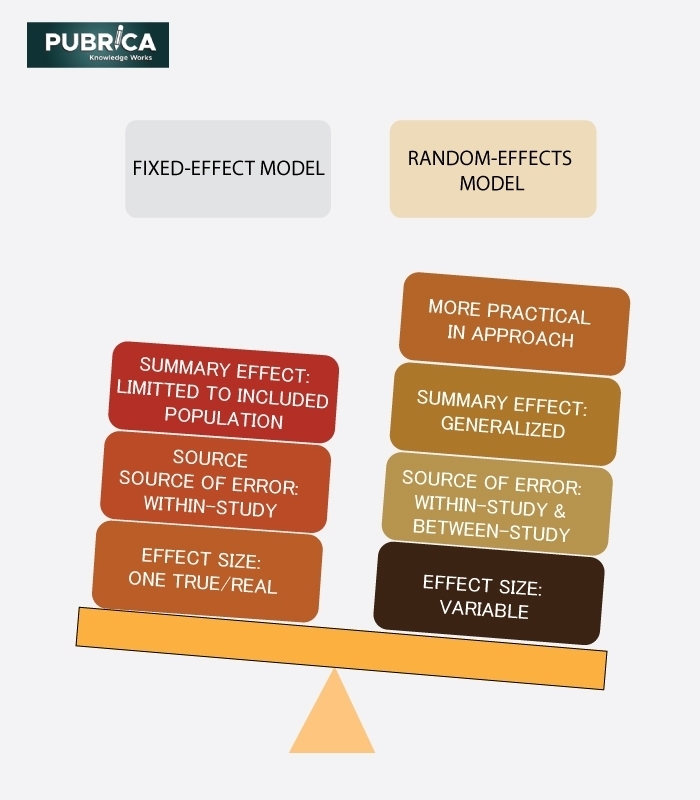
Laten we de basisprincipes bekijken. Beide modellen zijn ontworpen om met hiërarchische data om te gaan – data die in groepen is georganiseerd (zoals leerlingen in scholen, of campagnes in regio's). Het belangrijkste verschil zit in hoe ze deze groepen behandelen:

Fixed Effects

Een fixed effects model beschouwt de verschillen tussen de groepen als vaste en unieke effecten. Het model schat een apart effect voor elke groep. Denk aan de verschillende scholen in het lesmethoden voorbeeld. Het fixed effects model gaat ervan uit dat elke school een uniek, vast effect heeft op de schoolprestaties, en dat deze effecten niet toevallig zijn.

Analogie: Stel je voor dat je een groep bomen van verschillende soorten (eik, beuk, berk) observeert. Een fixed effects model zou de hoogte van elke specifieke boom meten en de verschillen tussen de hoogtes rechtstreeks vergelijken, zonder te generaliseren naar alle eiken, beuken of berken in het algemeen.

Wanneer te gebruiken: Gebruik een fixed effects model als je:

Geïnteresseerd bent in de effecten van de *specifieke* groepen die je hebt geobserveerd.
Denkt dat de groepen fundamenteel verschillend zijn en dat deze verschillen gecorreleerd zijn met andere variabelen in je model. (Dit is cruciaal om endogeniteit te voorkomen!)

Random Effects

Een random effects model behandelt de verschillen tussen de groepen als random variaties rond een gemeenschappelijk gemiddelde. In plaats van voor elke groep een apart effect te schatten, schat het model de variantie van de effecten tussen de groepen. Terug naar het lesmethoden voorbeeld: een random effects model zou aannemen dat de scholen een willekeurige steekproef zijn uit een grotere populatie van scholen, en dat de verschillen tussen de scholen toevallig zijn.

Analogie: Terug naar de bomen. Een random effects model zou de gemiddelde hoogte van elke soort boom (eik, beuk, berk) schatten en de variantie rond dat gemiddelde meten. Je bent dan niet geïnteresseerd in de individuele bomen, maar in de kenmerken van de soorten.

Wanneer te gebruiken: Gebruik een random effects model als je:

Geïnteresseerd bent in de variatie *tussen* de groepen en wilt generaliseren naar een grotere populatie van groepen.
Denkt dat de groepen een willekeurige steekproef zijn uit een grotere populatie.
Aan kunt nemen dat de effecten van de groepen ongecorreleerd zijn met andere variabelen in je model. (Dit is de cruciale onafhankelijkheidsaanname!)

De Onafhankelijkheidsaanname: Het Achilles hiel van Random Effects

De onafhankelijkheidsaanname van het random effects model is vaak het grootste struikelblok. Als de effecten van de groepen gecorreleerd zijn met andere variabelen in je model (bijvoorbeeld, de kwaliteit van de school is gecorreleerd met de socio-economische achtergrond van de leerlingen), dan kunnen de resultaten van het random effects model vertekend zijn. Dit heet endogeniteit.

Dit is waar het Hausman-test om de hoek komt kijken. De Hausman-test vergelijkt de resultaten van het fixed effects en het random effects model. Als er een significant verschil is, dan is dat een indicatie dat de onafhankelijkheidsaanname van het random effects model geschonden is, en dat je beter een fixed effects model kunt gebruiken.

Counterpoints: De Voordelen van Random Effects

Hoewel fixed effects modellen vaak de voorkeur genieten vanwege hun robuustheid tegen endogeniteit, hebben random effects modellen ook hun voordelen:

Efficiëntie: Random effects modellen kunnen efficiënter zijn dan fixed effects modellen, vooral als je veel groepen hebt. Dit betekent dat je kleinere standaardfouten krijgt, waardoor je meer power hebt om effecten te detecteren.
Generaliseerbaarheid: Random effects modellen laten je toe om te generaliseren naar een grotere populatie van groepen, wat met fixed effects modellen niet mogelijk is.
Mogelijkheid om tijd-invariante variabelen te analyseren: Fixed effects modellen "controleren" tijd-invariante variabelen (zoals geslacht of ras) binnen elke groep weg, omdat ze per definitie niet veranderen binnen die groep. Random effects modellen kunnen deze variabelen wel meenemen in de analyse.

Een Praktisch Stappenplan

Dus, hoe beslis je nu welk model te gebruiken? Hier is een praktisch stappenplan:

Definieer je onderzoeksvraag: Wat wil je precies weten? Ben je geïnteresseerd in de effecten van de *specifieke* groepen in je dataset, of wil je generaliseren naar een grotere populatie?
Evalueer de onafhankelijkheidsaanname: Is het aannemelijk dat de effecten van de groepen ongecorreleerd zijn met andere variabelen in je model? Denk na over mogelijke confounders.
Voer zowel een fixed effects als een random effects model uit.
Voer de Hausman-test uit: Is er een significant verschil tussen de resultaten van de twee modellen?
Interpreteer de resultaten zorgvuldig: Houd rekening met de sterke en zwakke punten van elk model bij het trekken van conclusies.

Meer dan alleen Statistiek

De keuze tussen fixed effects en random effects modellen is meer dan alleen een statistische beslissing. Het is een theoretische beslissing die reflecteert op je aannames over de data en de wereld. Denk goed na over je onderzoeksvraag en de context waarin je werkt.

Samenvattend:

Fixed effects: Unieke, vaste effecten per groep; robust tegen endogeniteit; beperkte generaliseerbaarheid.
Random effects: Willekeurige variaties rond een gemiddelde; efficiënt en generaliseerbaar; vereist de onafhankelijkheidsaanname.
Hausman-test: Helpt bij het bepalen of de onafhankelijkheidsaanname geschonden is.

Het is belangrijk om te onthouden dat er geen "one-size-fits-all" oplossing is. De beste keuze hangt af van je specifieke onderzoeksvraag, de kenmerken van je data, en je theoretische aannames.

We hopen dat dit artikel je geholpen heeft om de verschillen tussen fixed effects en random effects modellen beter te begrijpen. Denk eraan, je bent niet alleen. Statistiek kan uitdagend zijn, maar met de juiste tools en een beetje oefening kun je elk probleem aan.

Welke concrete stap ga jij nu zetten om je begrip van fixed en random effects modellen verder te verdiepen?