Hoe Bereken Je De Inhoud Van Een Kegel

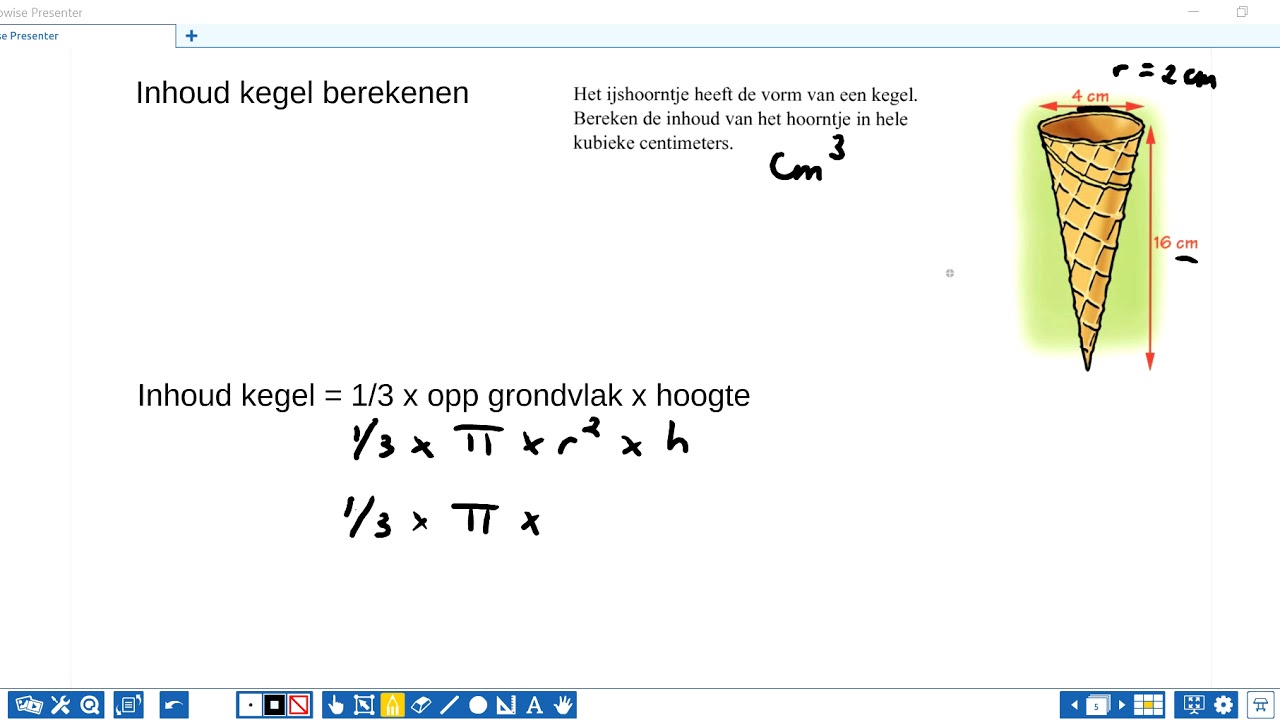
De kegel, een herkenbare vorm die we overal om ons heen zien, van ijshoorntjes tot verkeerskegels, is meer dan alleen een eenvoudige geometrische figuur. Het begrijpen van de inhoud van een kegel is niet alleen nuttig voor wiskundestudenten, maar ook voor iedereen die met ruimte, volume en ontwerp te maken heeft. In dit artikel duiken we diep in de formule en de stappen die nodig zijn om de inhoud van een kegel te berekenen, en we illustreren dit met concrete voorbeelden.

De Basis: Wat is een Kegel?

Laten we beginnen met een korte herhaling. Een kegel is een driedimensionale geometrische figuur die bestaat uit een plat vlak (de basis) en een punt (de top of apex) die verbonden zijn door een gebogen oppervlak. De basis is meestal een cirkel, maar kan in theorie ook een andere vorm hebben. We zullen ons hier echter concentreren op de meest voorkomende kegel: de rechte cirkelkegel, waarbij de top loodrecht boven het middelpunt van de cirkelvormige basis staat.

De Formule voor de Inhoud van een Kegel

De formule voor de inhoud van een kegel is relatief eenvoudig:

V = (1/3) * π * r² * h

Waar:

• V staat voor de inhoud van de kegel.
• π (pi) is een wiskundige constante, ongeveer gelijk aan 3.14159.
• r staat voor de straal van de cirkelvormige basis.
• h staat voor de hoogte van de kegel (de loodrechte afstand van de basis tot de top).

Het is cruciaal om te begrijpen dat de hoogte (h) loodrecht op de basis moet staan. Als je een schuine hoogte (de lengte van de zijkant van de kegel) hebt, moet je eerst de daadwerkelijke hoogte berekenen met behulp van de stelling van Pythagoras (a² + b² = c²).

Stap voor Stap: De Berekening

Laten we de formule eens in actie zien met een paar voorbeelden. We gaan stap voor stap door het proces, zodat je precies weet wat je moet doen.

Voorbeeld 1: Een Standaard Kegel

Stel dat we een kegel hebben met een straal (r) van 5 cm en een hoogte (h) van 10 cm. Laten we de inhoud berekenen:

1. Stap 1: Kwadrateer de straal: r² = 5² = 25 cm²
2. Stap 2: Vermenigvuldig met π: π * 25 cm² ≈ 3.14159 * 25 cm² ≈ 78.54 cm²
3. Stap 3: Vermenigvuldig met de hoogte: 78.54 cm² * 10 cm = 785.4 cm³
4. Stap 4: Deel door 3: 785.4 cm³ / 3 ≈ 261.8 cm³

De inhoud van de kegel is dus ongeveer 261.8 kubieke centimeter (cm³).

Voorbeeld 2: Een Kegel met een Diameter in plaats van een Straal

Soms krijg je de diameter van de basis in plaats van de straal. Herinner je eraan dat de straal de helft van de diameter is. Stel dat we een kegel hebben met een diameter van 8 meter en een hoogte van 12 meter.

1. Stap 1: Bereken de straal: r = diameter / 2 = 8 m / 2 = 4 m
2. Stap 2: Kwadrateer de straal: r² = 4² = 16 m²
3. Stap 3: Vermenigvuldig met π: π * 16 m² ≈ 3.14159 * 16 m² ≈ 50.27 m²
4. Stap 4: Vermenigvuldig met de hoogte: 50.27 m² * 12 m = 603.2 m³
5. Stap 5: Deel door 3: 603.2 m³ / 3 ≈ 201.1 m³

De inhoud van de kegel is dus ongeveer 201.1 kubieke meter (m³).

Voorbeeld 3: De Schuine Hoogte Gegeven

Dit is een iets complexer scenario. Stel dat we een kegel hebben met een straal van 6 cm en een schuine hoogte van 10 cm. We moeten eerst de echte hoogte berekenen met de stelling van Pythagoras.

De schuine hoogte (10 cm) is de hypotenusa van een rechthoekige driehoek, waarbij de straal (6 cm) de ene zijde is en de echte hoogte de andere zijde. Dus:

a² + b² = c²

6² + h² = 10²

36 + h² = 100

h² = 64

h = √64 = 8 cm

Nu we de hoogte hebben, kunnen we de inhoud berekenen:

1. Stap 1: Kwadrateer de straal: r² = 6² = 36 cm²
2. Stap 2: Vermenigvuldig met π: π * 36 cm² ≈ 3.14159 * 36 cm² ≈ 113.10 cm²
3. Stap 3: Vermenigvuldig met de hoogte: 113.10 cm² * 8 cm = 904.8 cm³
4. Stap 4: Deel door 3: 904.8 cm³ / 3 ≈ 301.6 cm³

De inhoud van de kegel is dus ongeveer 301.6 kubieke centimeter (cm³).

Real-World Voorbeelden en Toepassingen

Het berekenen van de inhoud van een kegel is meer dan alleen een wiskundige oefening. Het heeft praktische toepassingen in verschillende vakgebieden:

• Architectuur en Bouw: Architecten en ingenieurs gebruiken deze berekeningen om de hoeveelheid materialen te bepalen die nodig zijn voor kegelvormige daken, torens of funderingen.
• Productontwerp: Ontwerpers gebruiken de formule om de capaciteit van kegelvormige containers (zoals trechters of drinkbekers) te bepalen.
• Verkeersveiligheid: De inhoud van verkeerskegels kan worden gebruikt om hun stabiliteit te bepalen, afhankelijk van het materiaal waarmee ze gevuld zijn.
• Voedingsindustrie: Fabrikanten van ijs en andere voedingsmiddelen gebruiken de formule om de hoeveelheid product te bepalen die in een kegelvormige verpakking past.
• Wetenschap en Onderzoek: Onderzoekers kunnen deze berekeningen gebruiken bij het modelleren van verschillende natuurlijke fenomenen, zoals de vorm van vulkanen of de verspreiding van vloeistoffen in bepaalde apparatuur.

Stel je bijvoorbeeld voor dat een ijsverkoper wil weten hoeveel ijs hij nodig heeft om een groot aantal ijshoorntjes te vullen. Door de straal en de hoogte van de hoorntjes te meten, kan hij de totale benodigde hoeveelheid ijs nauwkeurig berekenen en verspilling voorkomen.

Een ander voorbeeld is een architect die een kegelvormig dak ontwerpt. Door de inhoud van de kegel te berekenen, kan hij bepalen hoeveel materialen (zoals hout of dakbedekking) hij nodig heeft, wat helpt bij het budgetteren en plannen van het project.

Belangrijke Punten om te Onthouden

Voordat je aan de slag gaat met het berekenen van de inhoud van kegels, zijn hier een paar belangrijke punten om te onthouden:

• Gebruik de juiste eenheden: Zorg ervoor dat alle metingen in dezelfde eenheden zijn (bijvoorbeeld centimeters, meters, inches). Als je verschillende eenheden hebt, converteer ze dan eerst.
• Gebruik de loodrechte hoogte: Verwar de schuine hoogte niet met de loodrechte hoogte. Gebruik de stelling van Pythagoras om de loodrechte hoogte te berekenen als je alleen de schuine hoogte hebt.
• Wees nauwkeurig met π: Gebruik een calculator met een π-knop voor de meest nauwkeurige resultaten. Anders kun je 3.14159 gebruiken als een goede benadering.
• Controleer je antwoord: Nadat je de berekening hebt voltooid, controleer dan of je antwoord logisch is. Een erg groot of klein getal kan duiden op een fout in je berekening.

Conclusie: De Kegel Ontrafeld

Het berekenen van de inhoud van een kegel is een fundamentele vaardigheid met diverse toepassingen. Door de formule te begrijpen en de stappen zorgvuldig te volgen, kun je nauwkeurige resultaten behalen en de inhoud van elke kegel bepalen. Of je nu een student bent die wiskunde studeert, een professional die aan een project werkt, of gewoon iemand die nieuwsgierig is naar de wereld om je heen, de kennis om de inhoud van een kegel te berekenen is waardevol en praktisch.

Dus, ga aan de slag, pak een rekenmachine en oefen met het berekenen van de inhoud van verschillende kegels. Je zult versteld staan van hoe vaak deze vaardigheid van pas kan komen!