Hoeveel Zijvlakken Heeft Een Kubus

Wist je dat een van de meest herkenbare en fundamentele geometrische vormen, de kubus, een verrassend eenvoudig concept is dat overal om ons heen te vinden is? Van de dobbelstenen op een spelbord tot de perfecte ijsblokjes in je drinken, de kubus is een alomaanwezige figuur. Maar heb je je ooit afgevraagd: "Hoeveel zijvlakken heeft een kubus eigenlijk?" Dit artikel duikt diep in de wereld van kubussen en beantwoordt die vraag, terwijl we tegelijkertijd de fascinerende eigenschappen van deze veelzijdige vorm verkennen.

Wat is een Kubus Eigenlijk?

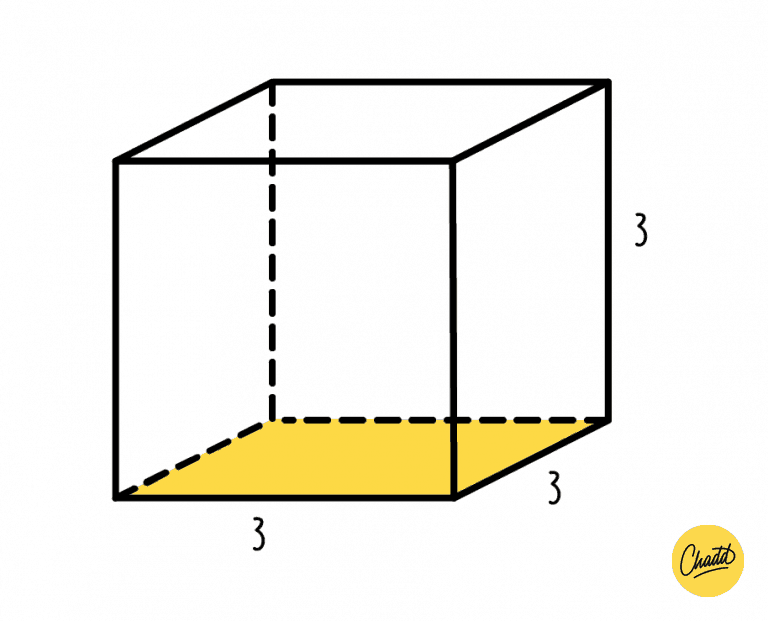
Voordat we direct ingaan op het aantal zijvlakken, laten we eerst eens duidelijk definiëren wat een kubus precies is. Een kubus is een driedimensionaal geometrisch object, ook wel een regelmatig hexaëder genoemd. Dit betekent dat het een vorm is met:

Zes vlakken
Alle vlakken zijn identieke vierkanten
Alle zijden zijn even lang
Alle hoeken zijn rechte hoeken (90 graden)

Denk aan een perfecte doos. Alle kanten zijn vierkant, en al die vierkanten zijn precies hetzelfde formaat. Dat is de essentie van een kubus.

Het Antwoord: Zes Zijvlakken

De vraag "Hoeveel zijvlakken heeft een kubus?" is eigenlijk al beantwoord in de definitie. Een kubus heeft zes zijvlakken. Elk van deze zijvlakken is een perfect vierkant. Stel je een Rubik's kubus voor. Je ziet zes gekleurde vlakken, elk verdeeld in kleinere vierkanten. Die zes vlakken representeren perfect de zes zijvlakken van een kubus.

Waarom Zes?

Het aantal zijvlakken, zes, is cruciaal voor de stabiliteit en de unieke eigenschappen van een kubus. Het zorgt ervoor dat de vorm in alle richtingen dezelfde is, wat de basis vormt voor veel toepassingen in de wiskunde, wetenschap en engineering.

Meer dan Alleen Zijvlakken: Andere Belangrijke Eigenschappen

Hoewel we ons voornamelijk richten op de zijvlakken, is het belangrijk om te weten dat een kubus meer is dan alleen zes vierkanten. Laten we enkele andere belangrijke eigenschappen bekijken:

Hoekpunten

Een kubus heeft acht hoekpunten. Dit zijn de punten waar de zijden van de vierkanten samenkomen. Stel je voor dat je een kubus bouwt met rietjes en klei. Je hebt acht stukjes klei nodig om de hoekpunten te vormen.

Ribben

Een kubus heeft twaalf ribben. Dit zijn de lijnen die de hoekpunten met elkaar verbinden en de randen van de vierkanten vormen. Elke ribbe verbindt twee hoekpunten.

Kubussen in de Wereld Om Ons Heen

Kubussen zijn overal om ons heen, vaak zonder dat we het beseffen. Laten we eens kijken naar enkele voorbeelden uit het dagelijks leven:

Dobbelstenen: De klassieke dobbelsteen is een perfecte kubus.
Suikerklontjes: Veel suikerklontjes zijn kubusvormig.
Verhuisdozen: Verhuisdozen zijn vaak (hoewel niet altijd perfect) kubusvormig.
Gebouwen: Veel moderne gebouwen hebben kubusvormige elementen in hun ontwerp.
Rubik's Kubus: Een iconisch speeltje dat de vorm van een kubus perfect illustreert.
IJsblokjes: De ijsblokjes in je drankje zijn vaak (of horen te zijn) perfect kubusvormig.

De eenvoudige vorm van de kubus maakt het een ideale bouwsteen in de architectuur en het ontwerp. Het is een efficiënte manier om ruimte te vullen en structuren te creëren.

Waarom is het Belangrijk om Dit te Weten?

Begrijpen hoeveel zijvlakken een kubus heeft, lijkt misschien een triviale vraag, maar het is een fundamenteel concept in de geometrie. Dit begrip legt de basis voor:

Ruimtelijk inzicht: Het helpt ons om objecten in drie dimensies beter te begrijpen.
Wiskunde: Het is cruciaal voor het berekenen van oppervlakte en volume.
Wetenschap: Het is belangrijk in de kristallografie, waar kristallen vaak kubusvormige structuren hebben.
Engineering: Het is essentieel bij het ontwerpen van structuren en machines.
Kunst en design: Kunstenaars en ontwerpers gebruiken kubussen om ruimtelijke relaties te creëren.

Kortom, het begrijpen van de basiskenmerken van een kubus is een bouwsteen voor een breder begrip van de wereld om ons heen.

Kubussen in Wiskunde: Oppervlakte en Volume

De zijvlakken van een kubus zijn essentieel voor het berekenen van de oppervlakte en het volume. Laten we deze concepten kort bekijken:

Oppervlakte

De oppervlakte van een kubus is de totale oppervlakte van alle zes zijvlakken. Omdat elk zijvlak een vierkant is, is de oppervlakte van één zijvlak gelijk aan de zijde in het kwadraat (s²). De totale oppervlakte van de kubus is dus 6 * s².

Formule: Oppervlakte = 6 * s² (waar 's' de lengte van een zijde is)

Volume

Het volume van een kubus is de hoeveelheid ruimte die de kubus inneemt. Het volume wordt berekend door de lengte, breedte en hoogte van de kubus met elkaar te vermenigvuldigen. Omdat alle zijden van een kubus even lang zijn, is het volume gelijk aan de zijde tot de derde macht (s³).

Formule: Volume = s³ (waar 's' de lengte van een zijde is)

Het begrijpen van deze formules stelt ons in staat om de hoeveelheid materiaal te berekenen die nodig is om een kubus te maken, of de hoeveelheid ruimte die een kubus inneemt. Dit is cruciaal in verschillende toepassingen, van het verpakken van producten tot het ontwerpen van gebouwen.

Een Interactieve Oefening

Laten we de theorie in de praktijk brengen. Pak een dobbelsteen of een suikerklontje (als je die bij de hand hebt). Kijk er eens goed naar. Tel de zijvlakken. Zie je de zes vierkanten? Bekijk de hoekpunten. Tel ze. Zijn het er inderdaad acht? Probeer de ribben te tellen. Kom je uit op twaalf? Door zelf actief met een kubus bezig te zijn, versterk je je begrip van de vorm en zijn eigenschappen.

Conclusie: De Kracht van de Eenvoud

We hebben nu vastgesteld dat een kubus zes zijvlakken heeft, evenals acht hoekpunten en twaalf ribben. Deze ogenschijnlijk eenvoudige geometrische vorm is de basis voor talloze toepassingen in de wiskunde, wetenschap, engineering en het dagelijks leven. Door de fundamentele eigenschappen van de kubus te begrijpen, verbeteren we ons ruimtelijk inzicht en leggen we een stevige basis voor verdere verkenningen in de wereld van de geometrie. Dus, de volgende keer dat je een kubus ziet, denk dan even na over de zes vierkanten die deze elegante vorm definiëren. Het is een bewijs van de kracht van de eenvoud in een complexe wereld. Bedankt voor het lezen!