Least Squares Fit In Excel

Laten we eerlijk zijn, data analyse kan soms voelen als een doolhof, zeker als je niet dagelijks met geavanceerde statistische software werkt. Je hebt een set data punten, je vermoedt een verband, maar hoe bewijs je dat? Hoe trek je de lijn – letterlijk en figuurlijk – die het beste bij die data past? Veel mensen worstelen hiermee, en voelen zich overweldigd door de complexe formules en software opties.

Least Squares Fit, of kleinste kwadraten methode, is een krachtige, maar relatief eenvoudige techniek om de beste passende lijn (of curve) door een set data punten te vinden. En ja, je kunt dit gewoon in Excel doen, zonder je zorgen te hoeven maken over ingewikkelde programmering of dure softwarepakketten. In dit artikel laten we je zien hoe. We focussen op praktische toepassingen en maken de theorie zo begrijpelijk mogelijk.

De Impact in de Praktijk: Verder dan de Theorie

Waarom zou je je druk maken over Least Squares Fit? Omdat het je helpt om inzichten te onttrekken uit je data. Stel je voor:

Je bent een marketingmanager en wilt weten of er een verband is tussen je advertentiebudget en je verkoopcijfers. Least Squares Fit kan je helpen om te voorspellen hoeveel je omzet zal stijgen als je je advertentiebudget verhoogt.
Je bent een projectmanager en wilt de geschatte duur van een project voorspellen op basis van historische data. Least Squares Fit kan je helpen om een realistisch tijdschema op te stellen en potentiële vertragingen te identificeren.
Je bent een onderzoeker die een wetenschappelijke hypothese test. Least Squares Fit kan je helpen om de sterkte van het verband tussen variabelen te kwantificeren en te bepalen of de resultaten significant zijn.

De mogelijkheden zijn eindeloos. Door de verbanden in je data te begrijpen, kun je betere beslissingen nemen en je resultaten verbeteren. Het gaat niet alleen om het plotten van een lijn op een grafiek; het gaat om het blootleggen van verborgen patronen die je business of onderzoek kunnen beïnvloeden.

De Kern: Wat is Least Squares Fit?

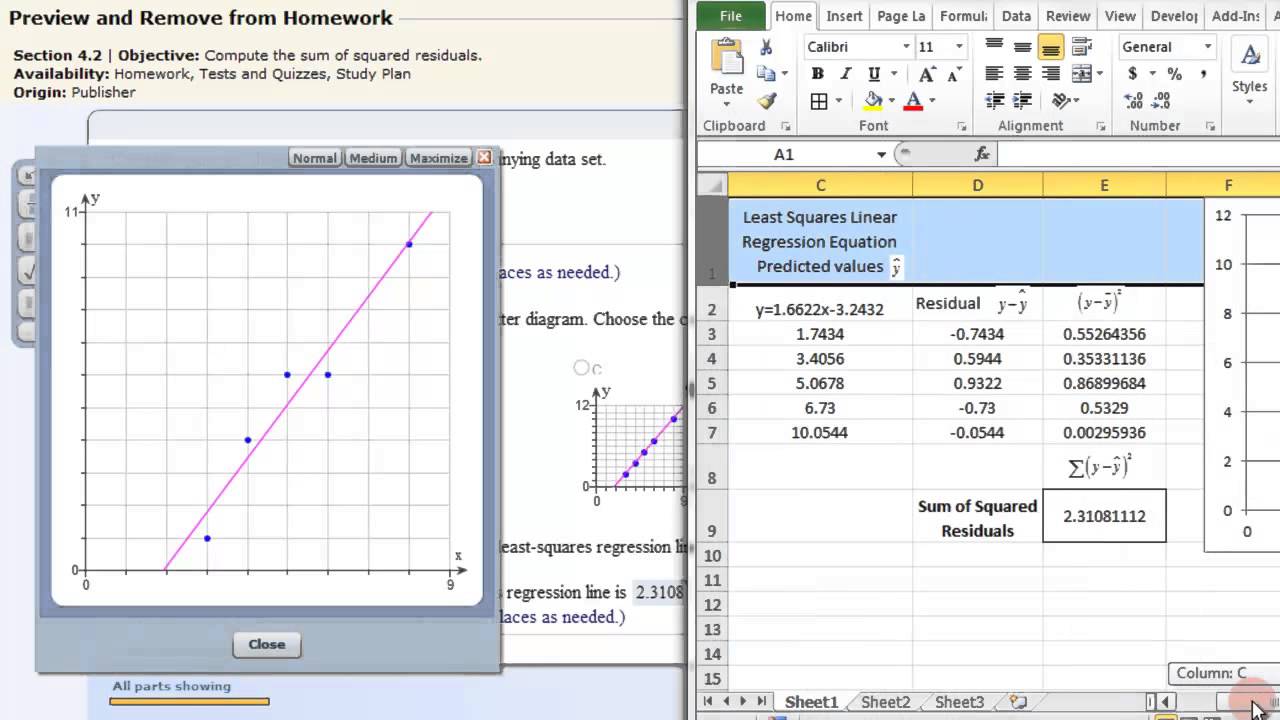
In essentie probeert Least Squares Fit de lijn (of curve) te vinden die de som van de gekwadrateerde afstanden tussen de data punten en de lijn minimaliseert. Klinkt ingewikkeld? Laten we het versimpelen.

Stel je voor dat je een aantal knikkers op een tafel gooit. Je wilt nu een rechte stok zo leggen dat hij zo dicht mogelijk bij alle knikkers ligt. Sommige knikkers zullen boven de stok liggen, andere eronder. De Least Squares Fit methode zoekt de positie van de stok waarbij de totale "afstand" tussen de knikkers en de stok zo klein mogelijk is. We kwadrateren die afstand (vandaar de naam "kleinste kwadraten") om ervoor te zorgen dat afstanden onder en boven de lijn even zwaar meetellen, en om negatieve waarden te vermijden. Dit garandeert dat we een evenwicht vinden, waarbij de lijn optimaal door de data loopt.

Het resultaat is een vergelijking van de vorm y = mx + b (voor een rechte lijn), waarbij:

y de afhankelijke variabele is (bijv. verkoopcijfers).
x de onafhankelijke variabele is (bijv. advertentiebudget).
m de helling van de lijn is (hoeveel y verandert voor elke eenheid verandering in x).
b het snijpunt met de y-as is (de waarde van y wanneer x gelijk is aan nul).

Counterpoint: Alternatieve Methoden en Hun Beperkingen

Er zijn alternatieve methoden om data te fitten, zoals de "Minimale Absolute Deviatie" methode. Deze methode minimaliseert de som van de absolute waarden van de afwijkingen, in plaats van de gekwadrateerde afwijkingen. Hoewel deze methode minder gevoelig is voor uitschieters, is de Least Squares methode vaak de voorkeur omdat hij wiskundig tractable is en een unieke oplossing garandeert. Andere, meer geavanceerde methoden bestaan ook, maar vereisen vaak specialistische software en een dieper begrip van statistiek.

Aan de Slag in Excel: Stap-voor-Stap

Nu de theorie duidelijk is, is het tijd om aan de slag te gaan in Excel. We zullen een eenvoudige lineaire regressie uitvoeren met behulp van de ingebouwde functies.

Bereid je data voor: Zorg ervoor dat je data in twee kolommen staat: een kolom voor de onafhankelijke variabele (x) en een kolom voor de afhankelijke variabele (y).
Scatter Plot: Selecteer je data en ga naar "Insert" > "Scatter (X, Y)" > "Scatter". Dit maakt een spreidingsdiagram van je data.
Trendline toevoegen: Klik op een van de data punten in de grafiek. Klik met de rechtermuisknop en selecteer "Add Trendline".
Trendline opties: Kies het type trendline dat je wilt gebruiken (meestal "Linear" voor een rechte lijn). Vink de vakjes aan voor "Display Equation on chart" en "Display R-squared value on chart".

De trendline verschijnt op de grafiek, samen met de vergelijking (y = mx + b) en de R-kwadraat waarde. De vergelijking geeft je de waarden van de helling (m) en het snijpunt (b), waarmee je de relatie tussen x en y kunt kwantificeren. De R-kwadraat waarde (tussen 0 en 1) geeft aan hoe goed de trendline bij de data past. Een waarde van 1 betekent een perfecte fit, terwijl een waarde van 0 betekent dat er geen lineair verband is.

Alternatieve Methoden in Excel: De LINEST Functie

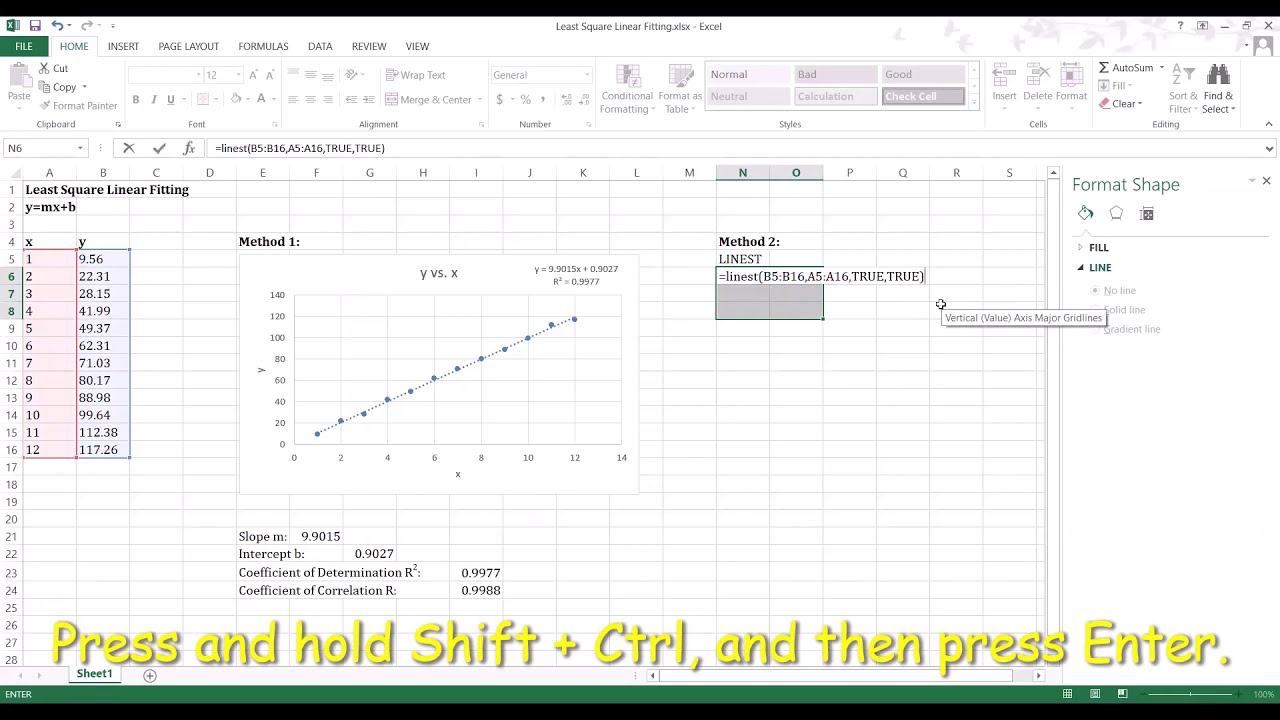
Excel biedt ook een krachtige functie genaamd LINEST, waarmee je niet alleen de helling en het snijpunt kunt berekenen, maar ook andere belangrijke statistische parameters. Zo gebruik je LINEST:

Selecteer een leeg bereik van 5 rijen hoog en ten minste 2 kolommen breed.
Typ de volgende formule in de bovenste cel van het geselecteerde bereik: =LINEST(bekende_y_waarden, bekende_x_waarden, [const], [stats]). Vervang bekende_y_waarden door het bereik van je y-data, en bekende_x_waarden door het bereik van je x-data. Laat [const] en [stats] weg (of vul ze in met respectievelijk WAAR of ONWAAR om de waarde van het snijpunt te forceren, of om meer statistische informatie te verkrijgen).
Druk op Ctrl+Shift+Enter (niet gewoon Enter!). Dit voert de formule uit als een array formule.

Het geselecteerde bereik zal nu gevuld zijn met verschillende statistische waarden, waaronder:

De helling (m) in de eerste cel.
Het snijpunt (b) in de tweede cel.
De standaardfout van de helling in de cel onder de helling.
De standaardfout van het snijpunt in de cel onder het snijpunt.
En nog veel meer statistische parameters die je kunnen helpen om de betrouwbaarheid van je model te beoordelen.

Wanneer Least Squares Fit Niet Werkt: Belangrijke Overwegingen

Hoewel Least Squares Fit een krachtige tool is, is het belangrijk om te onthouden dat het niet altijd de beste oplossing is. Hier zijn een paar belangrijke overwegingen:

Lineariteit: Least Squares Fit werkt het beste wanneer er een lineair verband is tussen de variabelen. Als het verband niet-lineair is, kun je proberen om de data te transformeren (bijv. door de logaritme te nemen van x of y) of een niet-lineaire regressiemethode te gebruiken.
Uitschieters: Uitschieters (data punten die ver verwijderd zijn van de rest van de data) kunnen een grote invloed hebben op de Least Squares Fit lijn. Het is belangrijk om uitschieters te identificeren en te onderzoeken, en te bepalen of ze verwijderd moeten worden (met de nodige voorzichtigheid).
Correlatie versus Causatie: Alleen omdat er een verband is tussen twee variabelen, betekent dit niet dat de ene variabele de andere veroorzaakt. Er kan een derde variabele zijn die beide variabelen beïnvloedt (een "lurking variable"). Wees voorzichtig met het trekken van causale conclusies op basis van Least Squares Fit.
Assumpties: Least Squares Fit is gebaseerd op een aantal aannames over de data, zoals de aanname dat de fouten (het verschil tussen de werkelijke waarden en de voorspelde waarden) normaal verdeeld zijn en een constante variantie hebben. Als deze aannames niet voldaan zijn, kunnen de resultaten onbetrouwbaar zijn.

Niet-lineaire relaties

Hoewel dit artikel zich voornamelijk richt op lineaire regressie, is het belangrijk te beseffen dat veel relaties in de echte wereld niet lineair zijn. Excel biedt ook de mogelijkheid om niet-lineaire trendlijnen toe te voegen aan je spreidingsdiagrammen, zoals exponentiële, logaritmische, polynomiale en power trendlijnen. Experimenteer met verschillende trendlijnen om te zien welke het beste bij je data past.

Samenvatting en Volgende Stappen

Least Squares Fit is een waardevolle techniek voor het analyseren van data en het identificeren van verbanden tussen variabelen. Met Excel kun je deze techniek eenvoudig toepassen zonder dat je specialistische statistische software nodig hebt. Door de stappen in dit artikel te volgen, kun je de beste passende lijn (of curve) door je data vinden en betere beslissingen nemen op basis van de verkregen inzichten.

Denk eraan dat het belangrijk is om de aannames van Least Squares Fit te begrijpen en de resultaten kritisch te beoordelen. Overweeg ook alternatieve methoden, zoals niet-lineaire regressie, als je data een niet-lineair verband vertoont.

Wat ga jij nu analyseren met Least Squares Fit in Excel? Welke verborgen patronen ga je ontdekken?