Levene's Test For Equality Of Variances

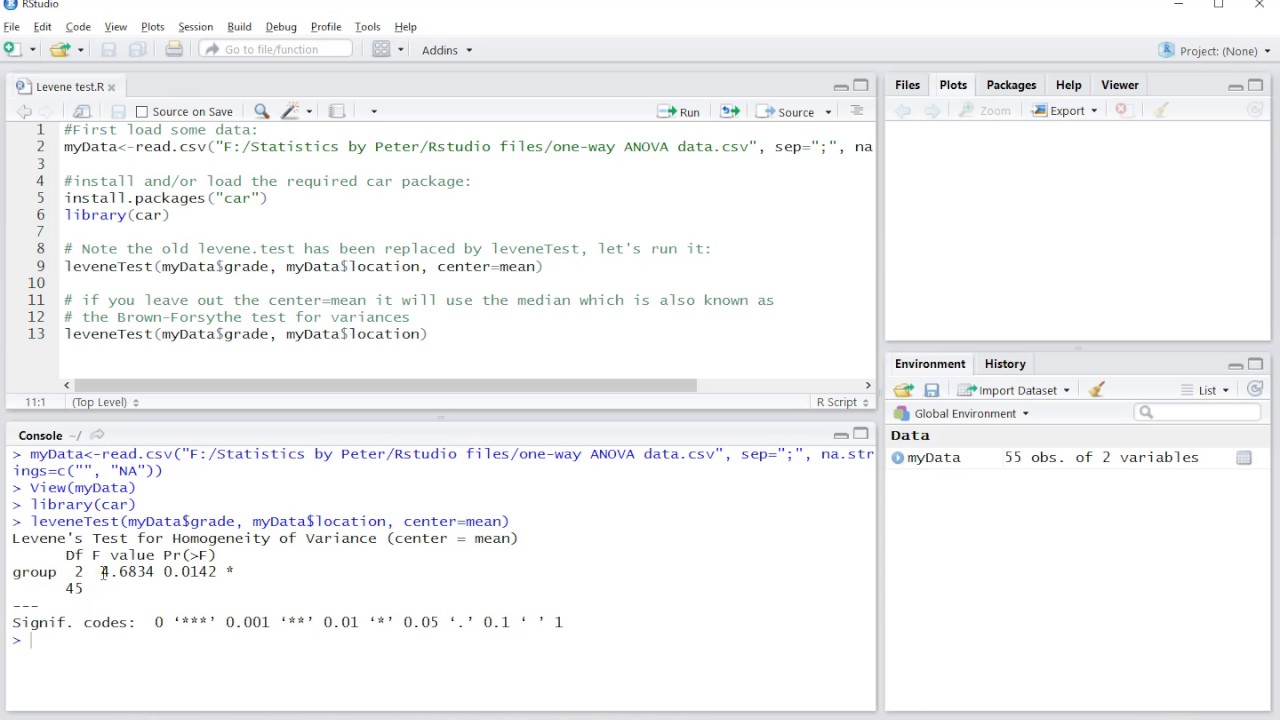
In de statistiek is het vaak cruciaal om de varianties van verschillende groepen te vergelijken. Een van de meest gebruikte methoden hiervoor is de Levene's test. Deze test is speciaal ontworpen om te beoordelen of de varianties van twee of meer groepen statistisch significant van elkaar verschillen. In dit artikel gaan we dieper in op Levene's test, de onderliggende principes, de toepassing ervan en een voorbeeld om het te illustreren.

Wat is Levene's Test?

Levene's test is een inferentiële statistische test die wordt gebruikt om de gelijkheid van varianties (of homogeniteit van varianties) te beoordelen tussen twee of meer groepen. Het is een belangrijke pre-conditie voor vele statistische tests, zoals de T-test en ANOVA (Analysis of Variance). Deze tests gaan ervan uit dat de varianties van de vergeleken groepen gelijk zijn. Wanneer deze aanname niet klopt, kunnen de resultaten van de tests onbetrouwbaar zijn. Levene's test is dus een cruciale stap in data-analyse om de validiteit van verdere analyses te waarborgen.

Belangrijkste Kenmerken

Levene's test staat bekend om zijn robustheid tegen afwijkingen van de normaliteitsassumptie. Dit betekent dat de test betrouwbare resultaten kan opleveren, zelfs als de data niet perfect normaal verdeeld is. Dit is een belangrijk voordeel ten opzichte van andere tests voor homogeniteit van varianties, zoals de Bartlett test, die zeer gevoelig is voor afwijkingen van normaliteit. De test werkt door een variantie-analyse (ANOVA) uit te voeren op de absolute afwijkingen van elke waarde ten opzichte van het groepsgemiddelde (of mediaan, afhankelijk van de gekozen variant van de test).

Wanneer Levene's Test Gebruiken?

Levene's test is geschikt wanneer je de volgende vragen wilt beantwoorden:

Zijn de varianties van de scores op een continue variabele significant verschillend tussen twee of meer onafhankelijke groepen?
Voldoen mijn data aan de aanname van homogeniteit van varianties, vereist voor het uitvoeren van een T-test of ANOVA?

Het is dus essentieel om de test uit te voeren vóór het uitvoeren van een T-test of ANOVA, om ervoor te zorgen dat de resultaten van deze tests valide zijn.

De Hypothesen

Levene's test formuleert de volgende hypothesen:

Nulhypothese (H0): De varianties van de groepen zijn gelijk.
Alternatieve hypothese (H1): Ten minste één van de varianties van de groepen is significant verschillend van de andere.

De p-waarde die uit Levene's test komt, wordt gebruikt om te bepalen of de nulhypothese verworpen kan worden. Als de p-waarde kleiner is dan het significantieniveau (meestal 0.05), wordt de nulhypothese verworpen en concludeert men dat de varianties significant verschillen.

De Procedure van Levene's Test

De algemene procedure voor het uitvoeren van Levene's test omvat de volgende stappen:

Bereken de absolute afwijkingen: Voor elke waarde in de dataset wordt de absolute afwijking van het groepsgemiddelde (of mediaan) berekend. De formule hiervoor is: |x_ij - μ_j|, waarbij x_ij de i-de waarde in groep j is en μ_j het gemiddelde van groep j is. Er bestaat ook een variant waarbij de mediaan wordt gebruikt in plaats van het gemiddelde. Dit maakt de test nog robuuster tegen outliers.
Voer een ANOVA uit op de absolute afwijkingen: Vervolgens wordt een ANOVA uitgevoerd op de berekende absolute afwijkingen. Dit levert een F-statistiek en een bijbehorende p-waarde op.
Interpreteer de p-waarde: Als de p-waarde kleiner is dan het gekozen significantieniveau (α), wordt de nulhypothese verworpen. Dit betekent dat er statistisch significant bewijs is dat de varianties van de groepen niet gelijk zijn.

Formules

Hoewel de meeste statistische software de berekeningen automatisch uitvoert, is het handig om de onderliggende formules te kennen. Zoals gezegd, wordt bij Levene's test een ANOVA uitgevoerd op de getransformeerde data. De belangrijkste berekeningen binnen ANOVA zijn:

Total Sum of Squares (SST): De totale variabiliteit in de dataset.
Between-Groups Sum of Squares (SSB): De variabiliteit tussen de groepen.
Within-Groups Sum of Squares (SSW): De variabiliteit binnen de groepen.
F-statistic: De ratio van de between-groups variance en de within-groups variance.

De p-waarde wordt dan berekend op basis van de F-statistic en de bijbehorende vrijheidsgraden.

Interpretatie van de Resultaten

De p-waarde is de sleutel tot het interpreteren van de resultaten van Levene's test. Zoals eerder gezegd:

p ≤ α (significantieniveau): Verwerp de nulhypothese. Concludeer dat de varianties van de groepen significant verschillen. Dit betekent dat je voorzichtig moet zijn bij het interpreteren van de resultaten van een T-test of ANOVA, en mogelijk alternatieve methoden moet overwegen die geen gelijke varianties vereisen (zoals een Welch's T-test).
p > α (significantieniveau): Accepteer de nulhypothese. Concludeer dat er geen significant bewijs is dat de varianties van de groepen verschillen. In dit geval kan je verder gaan met een T-test of ANOVA.

Real-World Voorbeeld

Stel je voor dat een onderzoeker wil onderzoeken of er een verschil is in de variabiliteit van de scores op een gestandaardiseerde test tussen leerlingen van verschillende scholen. De onderzoeker verzamelt data van drie scholen (A, B en C) en wil controleren of de varianties van de testscores gelijk zijn alvorens een ANOVA uit te voeren om te bepalen of er een significant verschil is in de gemiddelde testscores tussen de scholen.

Na het uitvoeren van Levene's test krijgt de onderzoeker een p-waarde van 0.02. Omdat dit kleiner is dan het significantieniveau van 0.05, verwerpt de onderzoeker de nulhypothese. Dit betekent dat er significant bewijs is dat de varianties van de testscores tussen de scholen niet gelijk zijn. De onderzoeker moet nu een alternatieve statistische test overwegen die geen gelijke varianties vereist, zoals de Welch's ANOVA, of een transformatie van de data uitvoeren om de varianties gelijk te maken.

Data Simulatie

Laten we dit illustreren met gesimuleerde data in R:


    # Simulatie van data
    set.seed(123) # Voor reproduceerbaarheid
    school_A <- rnorm(30, mean = 70, sd = 10)
    school_B <- rnorm(30, mean = 75, sd = 12)
    school_C <- rnorm(30, mean = 80, sd = 15)

    # Dataframe maken
    data <- data.frame(
      score = c(school_A, school_B, school_C),
      school = factor(rep(c("A", "B", "C"), each = 30))
    )

    # Levene's test uitvoeren
    library(car)
    leveneTest(score ~ school, data = data)

    # Output:
    # Levene's Test for Homogeneity of Variance (center = median)
    #       Df F value Pr(>F)
    # group  2  1.7858 0.1723
    #       87

In dit voorbeeld is de p-waarde (0.1723) groter dan 0.05. We verwerpen de nulhypothese dus niet. We concluderen dat er geen significant bewijs is dat de varianties tussen de scholen verschillen. We kunnen veilig een ANOVA uitvoeren om de gemiddelden te vergelijken.

Laten we een ander voorbeeld geven waar de varianties *wel* significant verschillen:


    # Simulatie van data met grotere variantie verschillen
    set.seed(456) # Andere seed voor ander resultaat
    school_A <- rnorm(30, mean = 70, sd = 5)
    school_B <- rnorm(30, mean = 75, sd = 10)
    school_C <- rnorm(30, mean = 80, sd = 20)

    # Dataframe maken
    data <- data.frame(
      score = c(school_A, school_B, school_C),
      school = factor(rep(c("A", "B", "C"), each = 30))
    )

    # Levene's test uitvoeren
    library(car)
    leveneTest(score ~ school, data = data)

    # Output (kan variëren afhankelijk van de seed):
    # Levene's Test for Homogeneity of Variance (center = median)
    #       Df F value    Pr(>F)
    # group  2  12.456  1.453e-05 ***
    #       87
    # ---
    # Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

In dit geval is de p-waarde (1.453e-05) significant kleiner dan 0.05. We verwerpen de nulhypothese. De varianties zijn significant verschillend. We zouden in dit geval geen reguliere ANOVA mogen gebruiken, maar een Welch's ANOVA of een ander alternatief.

Conclusie

Levene's test is een waardevol instrument om de aanname van homogeniteit van varianties te controleren voordat je verdergaat met andere statistische tests zoals T-tests en ANOVA. De robuustheid tegen afwijkingen van normaliteit maakt het een breed toepasbare test. Het correct interpreteren van de resultaten van Levene's test helpt je om de juiste statistische analyses te kiezen en betrouwbare conclusies te trekken uit je data. Dus, voordat je aan een T-test of ANOVA begint, vergeet niet om eerst Levene's test uit te voeren!