Midden Van Een Cirkel Bepalen

Wiskunde kan soms voelen als een doolhof, maar met de juiste begeleiding en uitleg kan het verrassend toegankelijk zijn. In dit artikel duiken we in een specifiek, maar essentieel onderwerp: het bepalen van het middelpunt van een cirkel. Dit is niet alleen nuttig voor wiskundestudenten, maar ook voor iedereen die geïnteresseerd is in geometrie, grafisch ontwerp, of zelfs basis engineering. We zullen de theorie achter deze berekening uitleggen, verschillende methoden presenteren en praktische voorbeelden geven. Dus, laten we samen de cirkel doorbreken en de geheimen van zijn middelpunt onthullen!

Waarom is het middelpunt van een cirkel bepalen belangrijk?

Het middelpunt van een cirkel is, zoals de naam al doet vermoeden, het exacte punt in het midden van de cirkel. Het bepalen van dit punt is cruciaal in verschillende toepassingen:

Geometrie: Het middelpunt is essentieel voor het construeren van cirkels met een bepaalde radius en het begrijpen van cirkelrelaties.
Grafisch ontwerp: Bij het creëren van logo's, illustraties en andere grafische elementen is het nauwkeurig plaatsen van cirkels en hun middelpunt vaak vereist.
Engineering: In de engineering wordt het middelpunt gebruikt voor het ontwerpen van onderdelen met ronde vormen, zoals lagers, assen en wielen.
Navigatie: Het concept van een middelpunt wordt gebruikt bij de bepaling van afstanden en posities op een bolvormig oppervlak, zoals de aarde.
Computer Graphics: In games en animaties zijn cirkels en hun middelpunt fundamentele bouwstenen.

Kortom, het begrijpen en kunnen bepalen van het middelpunt van een cirkel is een waardevolle vaardigheid met toepassingen in uiteenlopende disciplines.

Methoden om het middelpunt van een cirkel te bepalen

Er zijn verschillende methoden om het middelpunt van een cirkel te bepalen, afhankelijk van de beschikbare informatie. We zullen de meest voorkomende methoden hieronder bespreken:

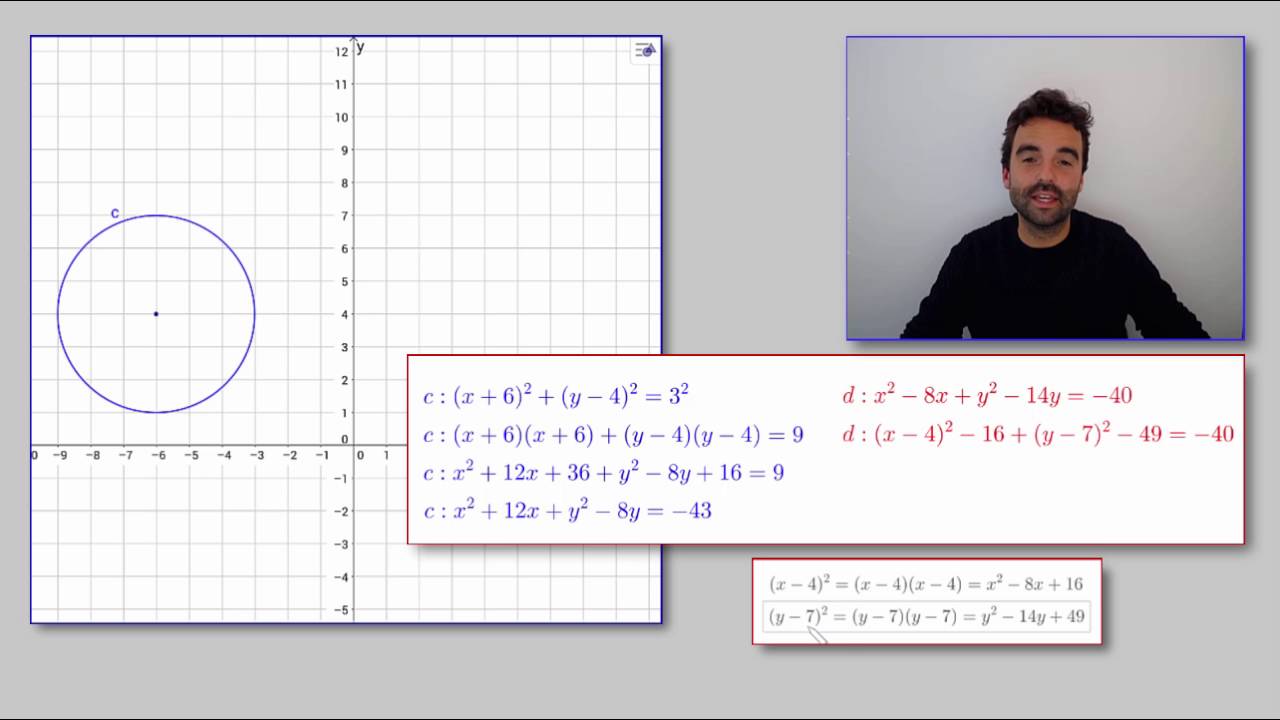
1. Gegeven de vergelijking van de cirkel

De algemene vergelijking van een cirkel is:

(x - a)² + (y - b)² = r²

Waar:

(a, b) de coördinaten van het middelpunt zijn.
r de radius van de cirkel is.

Als de vergelijking in deze vorm gegeven is, kunnen we het middelpunt direct aflezen. Bijvoorbeeld, als de vergelijking (x - 2)² + (y + 3)² = 9 is, dan is het middelpunt (2, -3) en de radius 3 (want √9 = 3).

Voorbeeld:

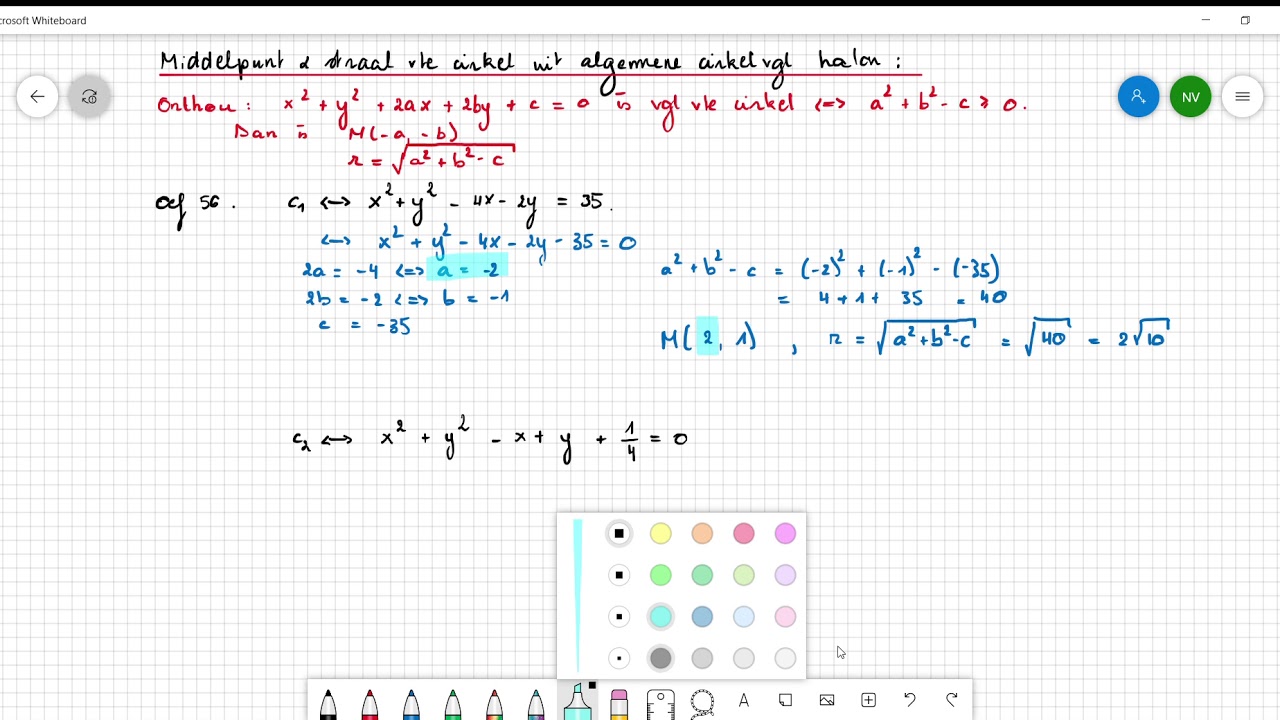
Stel, de vergelijking is x² + y² - 4x + 6y - 12 = 0. Om het middelpunt te vinden, moeten we de vergelijking herschrijven naar de standaardvorm. We doen dit door kwadraatafsplitsing:

Groepeer de x-termen en y-termen: (x² - 4x) + (y² + 6y) = 12
Vul de kwadraten aan: (x² - 4x + 4) + (y² + 6y + 9) = 12 + 4 + 9
Schrijf als kwadraten: (x - 2)² + (y + 3)² = 25

Nu kunnen we het middelpunt aflezen: (2, -3) en de radius: √25 = 5.

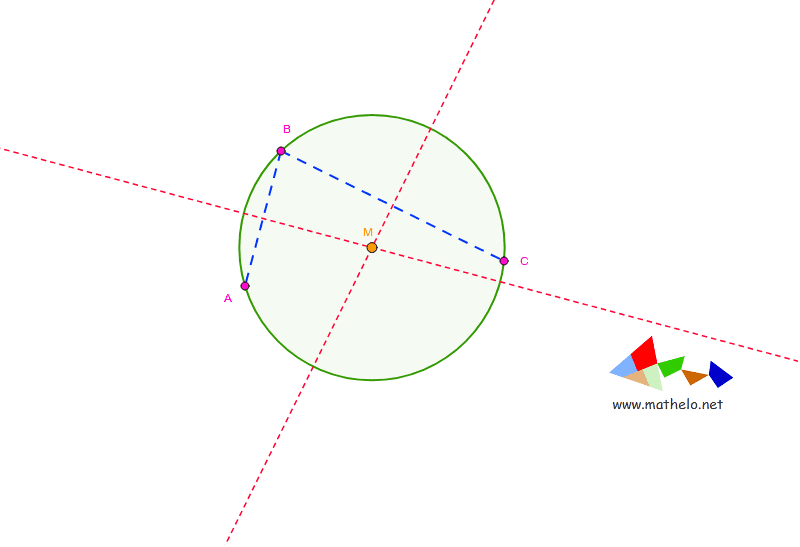
2. Gegeven drie punten op de cirkel

Deze methode maakt gebruik van het feit dat het middelpunt van een cirkel even ver van alle punten op de cirkel ligt. Met andere woorden, het middelpunt is het snijpunt van de middelloodlijnen van de lijnen die de punten verbinden.

Stappen:

Kies twee lijnen: Kies twee paren punten uit de drie gegeven punten (bijvoorbeeld AB en BC).
Bepaal de middens: Bereken het midden van elke lijn. Het midden van lijn AB is ((Ax + Bx)/2, (Ay + By)/2).
Bepaal de hellingen: Bereken de helling van elke lijn. De helling van lijn AB is (By - Ay)/(Bx - Ax).
Bepaal de hellingen van de middelloodlijnen: De helling van de middelloodlijn is de negatieve inverse van de helling van de lijn. Bijvoorbeeld, als de helling van AB m is, dan is de helling van de middelloodlijn -1/m.
Bepaal de vergelijkingen van de middelloodlijnen: Gebruik de punt-helling vorm van een lijn (y - y1 = m(x - x1)) om de vergelijkingen van de middelloodlijnen te bepalen, waarbij (x1, y1) het midden van de lijn is en m de helling van de middelloodlijn.
Los het stelsel van vergelijkingen op: Los het stelsel van de twee vergelijkingen van de middelloodlijnen op om de coördinaten van het snijpunt te vinden. Dit snijpunt is het middelpunt van de cirkel.

Voorbeeld:

Gegeven de punten A(1, 1), B(5, 1) en C(3, 5). We bepalen de middelloodlijn van AB en BC.

Middelloodlijn van AB:
- Midden van AB: ((1+5)/2, (1+1)/2) = (3, 1)
- Helling van AB: (1-1)/(5-1) = 0
- Helling van de middelloodlijn: Oneindig (verticale lijn)
- Vergelijking van de middelloodlijn: x = 3
Middelloodlijn van BC:
- Midden van BC: ((5+3)/2, (1+5)/2) = (4, 3)
- Helling van BC: (5-1)/(3-5) = -2
- Helling van de middelloodlijn: 1/2
- Vergelijking van de middelloodlijn: y - 3 = (1/2)(x - 4) => y = (1/2)x + 1

Nu lossen we het stelsel op:

x = 3
y = (1/2)x + 1

Substitueer x = 3 in de tweede vergelijking: y = (1/2)(3) + 1 = 2.5

Dus, het middelpunt van de cirkel is (3, 2.5).

3. Geometrische constructie

Als je een passer en een liniaal hebt, kun je het middelpunt ook geometrisch construeren:

Teken twee koorden: Teken twee willekeurige koorden (lijnstukken die twee punten op de cirkel verbinden) die niet parallel zijn.
Construeer de middelloodlijnen: Construeer de middelloodlijn van elke koorde. Dit doe je door de passer op elk eindpunt van de koorde te zetten en bogen te tekenen die elkaar kruisen. Verbind de kruispunten van de bogen.
Het snijpunt is het middelpunt: Het snijpunt van de twee middelloodlijnen is het middelpunt van de cirkel.

Deze methode is gebaseerd op het feit dat de middelloodlijn van een koorde altijd door het middelpunt van de cirkel gaat.

Praktische voorbeelden

Laten we eens kijken naar een paar praktische voorbeelden om het bepalen van het middelpunt van een cirkel te illustreren:

Voorbeeld 1:

Je bent een grafisch ontwerper en je moet een logo ontwerpen met een perfecte cirkel. Je hebt een deel van de cirkel al getekend, maar je weet het middelpunt niet. Je kunt de geometrische constructiemethode gebruiken om het middelpunt te vinden en de cirkel te voltooien.

Voorbeeld 2:

Je werkt als ingenieur aan het ontwerp van een machineonderdeel. Je hebt drie meetpunten op een bestaand rond onderdeel. Om de specificaties van het onderdeel te bepalen, moet je het middelpunt van de cirkel bepalen die door deze punten gaat. Je kunt de methode met drie punten gebruiken om de exacte locatie van het middelpunt te berekenen.

Voorbeeld 3:

Je bent een student wiskunde en je krijgt de vergelijking van een cirkel: x² + y² + 2x - 4y - 4 = 0. Je moet het middelpunt en de radius van de cirkel bepalen. Je kunt de methode met de vergelijking van de cirkel gebruiken om de vergelijking te herschrijven naar de standaardvorm en het middelpunt en de radius af te lezen.

Tips en trucs

Hier zijn een paar tips en trucs die je kunnen helpen bij het bepalen van het middelpunt van een cirkel:

Visualiseer het probleem: Maak een schets van de cirkel en de beschikbare informatie. Dit kan je helpen om de juiste methode te kiezen.
Controleer je antwoord: Als je eenmaal het middelpunt hebt berekend, controleer dan of het middelpunt inderdaad even ver van alle punten op de cirkel ligt (indien van toepassing).
Gebruik software: Er zijn verschillende softwareprogramma's en online calculators beschikbaar die je kunnen helpen bij het bepalen van het middelpunt van een cirkel.
Oefening baart kunst: Hoe meer je oefent met het bepalen van het middelpunt van een cirkel, hoe gemakkelijker het zal worden.

Conclusie

Het bepalen van het middelpunt van een cirkel is een fundamentele vaardigheid in de wiskunde en heeft praktische toepassingen in diverse disciplines. We hebben verschillende methoden besproken, waaronder het gebruik van de vergelijking van de cirkel, het werken met drie punten op de cirkel en het toepassen van geometrische constructie. Door de theorie te begrijpen en de stappen zorgvuldig te volgen, kun je nauwkeurig het middelpunt van elke cirkel bepalen. Hopelijk heeft dit artikel je geholpen om je begrip van cirkels en hun eigenschappen te verdiepen. Blijf oefenen en experimenteren met deze methoden, en je zult merken dat wiskunde steeds minder als een doolhof aanvoelt en steeds meer als een boeiende ontdekkingstocht.

Dus, pak je passer en liniaal, of duik in de wiskundige formules, en begin met het ontdekken van de verborgen middens in de wereld om je heen!