Partial And Semi Partial Correlation

Heb je je ooit afgevraagd hoe je de echte relatie tussen twee variabelen kunt ontdekken, terwijl je de invloed van andere, verstorende factoren wegneemt? In de wereld van statistiek en data-analyse stuiten we vaak op complexe situaties waarin variabelen met elkaar verbonden zijn, maar niet op de manier die we aanvankelijk dachten. Dit artikel is bedoeld voor studenten, onderzoekers en professionals die een beter begrip willen krijgen van de concepten partiële en semi-partiële correlatie, en hoe deze technieken hen kunnen helpen om meer accurate en zinvolle conclusies te trekken uit hun data. We gaan dieper in op de theorie, de toepassing en de interpretatie van deze krachtige tools. Bereid je voor om je statistische vaardigheden naar een hoger niveau te tillen!

Wat is Correlatie, en Waarom is het Soms Misleidend?

Voordat we in de wereld van partiële en semi-partiële correlatie duiken, is het belangrijk om even stil te staan bij het basisconcept van correlatie. Correlatie meet de sterkte en de richting van de lineaire relatie tussen twee variabelen. Een positieve correlatie betekent dat als de ene variabele toeneemt, de andere ook toeneemt, terwijl een negatieve correlatie betekent dat als de ene variabele toeneemt, de andere afneemt. De correlatiecoëfficiënt, meestal aangeduid met r, varieert van -1 tot +1, waarbij -1 een perfecte negatieve correlatie aangeeft, +1 een perfecte positieve correlatie, en 0 geen lineaire correlatie.

Maar hier is de crux: correlatie betekent geen causaliteit. Een sterke correlatie tussen twee variabelen betekent niet noodzakelijk dat de ene variabele de andere veroorzaakt. Er kan een derde, verstorende variabele in het spel zijn die beide variabelen beïnvloedt. Dit noemen we een confounder of een lurking variable. Het negeren van deze verstorende variabelen kan leiden tot misleidende conclusies over de relatie tussen de variabelen waarin we werkelijk geïnteresseerd zijn.

Voorbeeld: Stel dat je een sterke positieve correlatie vindt tussen de verkoop van ijsjes en het aantal verdrinkingen in de zomer. Betekent dit dat ijsjes verdrinkingen veroorzaken? Natuurlijk niet! De verstorende variabele is hier de temperatuur. Hogere temperaturen leiden zowel tot een toename van de ijsverkoop als tot meer mensen die gaan zwemmen, wat het risico op verdrinking vergroot.

De Redder in Nood: Partiële Correlatie

Partiële correlatie is een statistische techniek die ons helpt om de spurious (onechte) correlatie tussen twee variabelen te elimineren, door de invloed van een of meer andere variabelen, de zogenaamde controlevariabelen, constant te houden. Met andere woorden, we proberen de relatie tussen twee variabelen te isoleren, alsof de controlevariabelen geen rol spelen.

Hoe Werkt het?

In essentie berekent partiële correlatie de correlatie tussen twee variabelen, nadat hun respectievelijke lineaire relaties met de controlevariabelen zijn verwijderd. Dit wordt vaak gedaan door middel van regressie. We voeren regressies uit waarbij elke van de twee variabelen wordt voorspeld door de controlevariabelen. De residuen (het verschil tussen de werkelijke en voorspelde waarden) van deze regressies vertegenwoordigen het deel van elke variabele dat niet kan worden verklaard door de controlevariabelen. De correlatie tussen deze residuen is de partiële correlatie.

Formule (voor één controlevariabele Z):

r_XY.Z = (r_XY - r_XZ * r_YZ) / √((1 - r_XZ²) * (1 - r_YZ²))

Waar:

• r_XY.Z is de partiële correlatie tussen X en Y, gecontroleerd voor Z
• r_XY is de bivariate correlatie tussen X en Y
• r_XZ is de bivariate correlatie tussen X en Z
• r_YZ is de bivariate correlatie tussen Y en Z

Wanneer Gebruik je Partiële Correlatie?

Partiële correlatie is nuttig in de volgende situaties:

• Onderzoek naar Causale Relaties: Wanneer je een vermoeden hebt van een causale relatie tussen twee variabelen, maar je wilt er zeker van zijn dat de relatie niet wordt verklaard door een derde variabele.
• Het Identificeren van Spurious Correlaties: Wanneer je een sterke correlatie vindt tussen twee variabelen, maar je vermoedt dat deze wordt veroorzaakt door een gemeenschappelijke oorzaak.
• Het Verfijnen van Modellen: In regressiemodellen kan partiële correlatie helpen om te bepalen welke variabelen echt significant bijdragen aan de voorspelling van de afhankelijke variabele.

Terug naar het ijsjes voorbeeld: Als we de partiële correlatie berekenen tussen de ijsverkoop en het aantal verdrinkingen, gecontroleerd voor de temperatuur, zullen we waarschijnlijk een correlatie vinden die veel zwakker is, of zelfs verdwijnt. Dit suggereert dat de oorspronkelijke correlatie spurious was, en dat de temperatuur de echte verklaring is voor de relatie tussen de twee variabelen.

Semi-Partiële Correlatie: Een Subtiele, Maar Belangrijke Uitzondering

Semi-partiële correlatie, ook wel bekend als part correlatie, is een variant op partiële correlatie, maar met een belangrijk verschil. In plaats van de invloed van de controlevariabele(n) op beide variabelen te verwijderen, verwijderen we de invloed alleen van de controlevariabele(n) op één van de variabelen. De andere variabele blijft onaangetast.

Hoe Werkt het?

Net als bij partiële correlatie, gebruiken we regressie. We voeren een regressie uit waarbij één van de variabelen (bijvoorbeeld Y) wordt voorspeld door de controlevariabelen. De residuen van deze regressie vertegenwoordigen het deel van Y dat niet kan worden verklaard door de controlevariabelen. Vervolgens berekenen we de correlatie tussen deze residuen en de originele waarden van de andere variabele (X). X is dus niet gecorrigeerd voor de invloed van de controlevariabelen.

Formule (voor één controlevariabele Z, waarbij Z van Y wordt verwijderd):

r_X(Y.Z) = (r_XY - r_XZ * r_YZ) / √(1 - r_YZ²)

Waar:

• r_X(Y.Z) is de semi-partiële correlatie tussen X en Y, waarbij de invloed van Z is verwijderd van Y
• r_XY is de bivariate correlatie tussen X en Y
• r_XZ is de bivariate correlatie tussen X en Z
• r_YZ is de bivariate correlatie tussen Y en Z

Wanneer Gebruik je Semi-Partiële Correlatie?

Semi-partiële correlatie is nuttig wanneer je de unieke bijdrage van een variabele wilt bepalen aan de variabiliteit in een andere variabele, na het wegvangen van de invloed van andere variabelen. Het wordt vaak gebruikt in regressieanalyse om te bepalen hoeveel variantie in de afhankelijke variabele uniek wordt verklaard door elke onafhankelijke variabele, bovenop de variantie die al wordt verklaard door andere onafhankelijke variabelen.

Voorbeeld: Stel dat we willen weten hoeveel van de variantie in prestaties op het werk uniek wordt verklaard door intelligentie, na het controleren voor opleidingsniveau. We zouden een semi-partiële correlatie berekenen tussen intelligentie en prestaties op het werk, waarbij de invloed van opleidingsniveau van prestaties op het werk wordt verwijderd. Dit geeft ons een indicatie van de extra bijdrage van intelligentie aan de verklaring van prestaties op het werk, bovenop de bijdrage van opleidingsniveau.

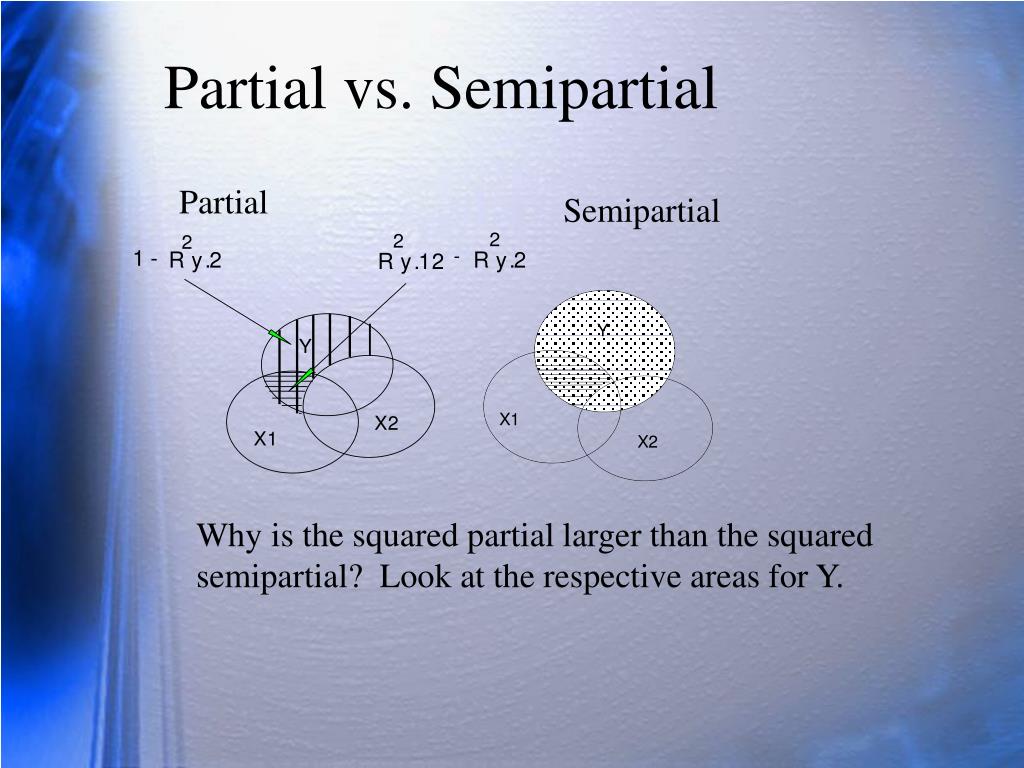
Het Belangrijkste Verschil: Partiële vs. Semi-Partiële Correlatie

Het sleutelverschil tussen partiële en semi-partiële correlatie ligt in het feit dat bij partiële correlatie de invloed van de controlevariabelen van beide variabelen wordt verwijderd, terwijl bij semi-partiële correlatie de invloed van de controlevariabelen slechts van één variabele wordt verwijderd.

Hier is een overzicht:

• Partiële Correlatie: Meet de relatie tussen X en Y, na het verwijderen van de invloed van Z op zowel X als Y. Focust op de correlatie tussen de residuen van beide regressies.
• Semi-Partiële Correlatie: Meet de relatie tussen X en Y, na het verwijderen van de invloed van Z alleen op Y. Focust op de correlatie tussen de originele waarde van X en het residu van de regressie van Y op Z.

Praktische Overwegingen en Valkuilen

Hoewel partiële en semi-partiële correlatie krachtige tools zijn, is het belangrijk om ze met de nodige voorzichtigheid te gebruiken:

• Lineariteit: De technieken zijn gebaseerd op de aanname van lineaire relaties tussen de variabelen. Als de relaties niet-lineair zijn, kunnen de resultaten misleidend zijn.
• Aannames van Regressie: De validiteit van de resultaten is afhankelijk van de validiteit van de aannames van de gebruikte regressiemodellen (bijvoorbeeld normaliteit van de residuen, homoscedasticiteit).
• Interpretatie: Het is cruciaal om de resultaten correct te interpreteren. Een partiële of semi-partiële correlatie die dicht bij nul ligt, betekent niet noodzakelijk dat er geen relatie is tussen de variabelen. Het kan betekenen dat de relatie volledig wordt verklaard door de controlevariabelen, of dat de relatie niet-lineair is.
• Multicollineariteit: Als de controlevariabelen sterk met elkaar correleren (multicollineariteit), kan dit de stabiliteit en interpreteerbaarheid van de resultaten beïnvloeden.
• Theoretisch Kader: De keuze van de controlevariabelen moet gebaseerd zijn op een sterk theoretisch kader. Het willekeurig toevoegen van controlevariabelen kan leiden tot onzinnige resultaten.

Conclusie: Meer Zicht Op Zuivere Relaties

Partiële en semi-partiële correlatie zijn onmisbare tools voor onderzoekers en data-analisten die op zoek zijn naar de echte relaties tussen variabelen. Door de invloed van verstorende factoren weg te nemen, kunnen we een beter begrip krijgen van de onderliggende mechanismen die onze data drijven. Of je nu de causale relatie tussen variabelen wilt onderzoeken, spurious correlaties wilt identificeren, of regressiemodellen wilt verfijnen, deze technieken bieden een krachtige manier om meer accurate en zinvolle conclusies te trekken. Vergeet niet om de aannames te controleren, de resultaten zorgvuldig te interpreteren, en je analyses te baseren op een sterk theoretisch kader. Met deze tools in je arsenaal ben je goed uitgerust om de complexiteit van data-analyse te navigeren en waardevolle inzichten te onthullen.