Statics And Mechanics Of Materials In Si Units

In de wereld van de ingenieurswetenschappen spelen Statica en Mechanica van Materialen een cruciale rol. Deze disciplines vormen de basis voor het begrijpen van hoe structuren en componenten reageren op krachten en belastingen. Het gebruik van SI-eenheden (Système International d'Unités) is essentieel voor een consistente en internationaal erkende benadering van deze analyses. Dit artikel duikt dieper in de concepten van Statica en Mechanica van Materialen, met speciale aandacht voor hun toepassing in SI-eenheden.

Statica: Evenwicht en Krachten

Statica is de tak van de mechanica die zich bezighoudt met lichamen in rust, oftewel in statisch evenwicht. Een lichaam is in statisch evenwicht wanneer de som van alle krachten en momenten die erop inwerken gelijk is aan nul. Dit principe is fundamenteel voor het ontwerpen van veilige en stabiele structuren.

De Basisprincipes van Statica

De belangrijkste concepten in statica zijn:

Kracht: Een vectorgrootheid die een invloed beschrijft die de beweging van een object kan veranderen. Gemeten in Newton (N) in SI-eenheden.
Moment (Koppel): De neiging van een kracht om een object om een as te laten roteren. Gemeten in Newton-meter (N·m).
Evenwichtsvoorwaarden: ∑F = 0 (de som van alle krachten in alle richtingen is nul) en ∑M = 0 (de som van alle momenten om elk punt is nul).
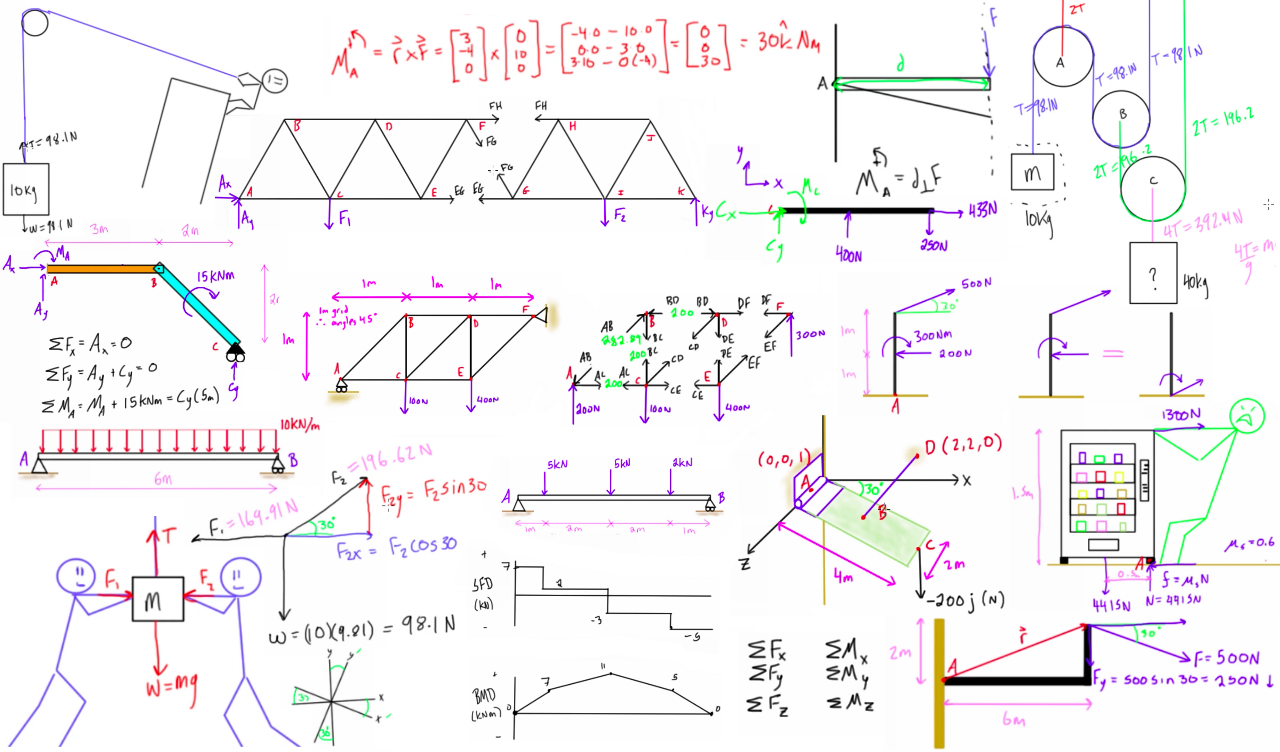
Vrijlichaamdiagram (VLD): Een schematische weergave van een object, geïsoleerd van zijn omgeving, waarop alle krachten en momenten die erop inwerken zijn aangegeven. Essentieel voor het oplossen van statica problemen.

Het correct opstellen van een VLD is cruciaal. Het helpt bij het visualiseren van alle krachten, reacties en momenten die op het lichaam inwerken, waardoor het eenvoudiger wordt om de evenwichtsvoorwaarden toe te passen.

Toepassingen van Statica

Statica is van vitaal belang in diverse engineering disciplines, waaronder:

Civiele Techniek: Ontwerpen van bruggen, gebouwen en andere infrastructurele werken. Bijvoorbeeld, bij het ontwerpen van een brug, moet de belasting van voertuigen, windkracht en het gewicht van de brug zelf worden overwogen om te garanderen dat de brug stabiel blijft en niet instort.
Werktuigbouwkunde: Ontwerpen van machines en mechanische systemen, waarbij de statische krachten op componenten moeten worden geanalyseerd om ervoor te zorgen dat ze niet falen. Denk aan het ontwerp van een kraanarm, waar de krachten als gevolg van de belasting, het gewicht van de arm zelf en de reactiekrachten in de steunpunten nauwkeurig moeten worden berekend.
Lucht- en Ruimtevaarttechniek: Analyseren van de krachten die inwerken op vliegtuigen en ruimteschepen, zowel in rust als tijdens de vlucht.

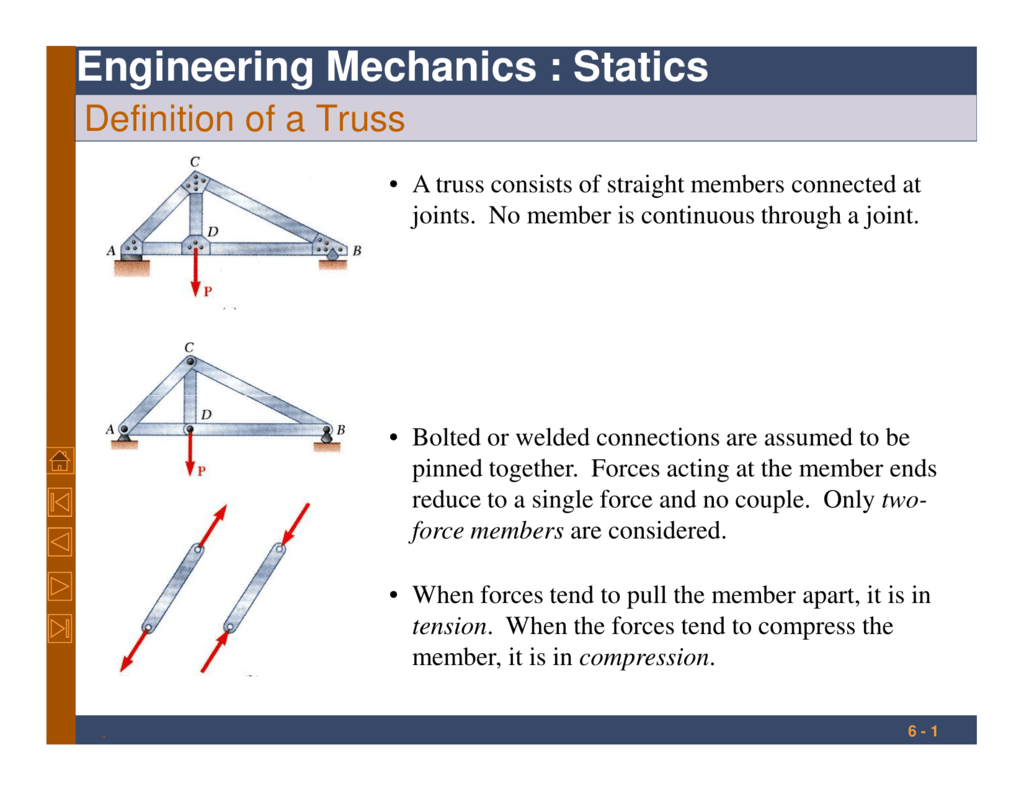
Een concreet voorbeeld is de analyse van een vakwerkconstructie. Vakwerken worden vaak gebruikt in bruggen en daken. Statica wordt gebruikt om de krachten in elke staaf van het vakwerk te bepalen. Door de evenwichtsvoorwaarden toe te passen op elk knooppunt (waar de staven samenkomen), kunnen de trek- en drukkrachten in de staven worden berekend. Deze informatie is essentieel om te bepalen of de staven sterk genoeg zijn om de verwachte belastingen te weerstaan.

Mechanica van Materialen: Spanning, Rek en Vervorming

Mechanica van Materialen (ook bekend als sterkteleer) gaat een stap verder dan statica door de interne spanningen en rekken in vaste stoffen te onderzoeken als gevolg van externe belastingen. Het onderzoekt hoe materialen reageren op deze spanningen en rekken, en hoe ze vervormen en mogelijk falen.

Belangrijke Concepten in Mechanica van Materialen

Enkele kernconcepten zijn:

Spanning (σ): De interne kracht die werkt op een doorsnede van een object, gedeeld door het oppervlak van die doorsnede. Gemeten in Pascal (Pa) of N/m² in SI-eenheden. Belangrijk om te onthouden dat 1 MPa = 1 N/mm².
Rek (ε): De verhouding van de verandering in lengte tot de oorspronkelijke lengte van een object. Een dimensieloze grootheid.
Elasticiteitsmodulus (E): Een materiaaleigenschap die de stijfheid van een materiaal beschrijft. Het is de verhouding tussen spanning en rek in het elastische gebied van het materiaal. Gemeten in Pascal (Pa).
Poisson's ratio (ν): Een materiaaleigenschap die de verhouding beschrijft tussen de laterale rek en de axiale rek. Een dimensieloze grootheid.
Vloeigrens (σ_v): De spanning waarbij een materiaal begint te plastisch te vervormen (blijvend vervormt).
Treksterkte (σ_t): De maximale spanning die een materiaal kan weerstaan voordat het begint te breken.

De relatie tussen spanning en rek wordt vaak beschreven door de wet van Hooke, die stelt dat spanning recht evenredig is met rek in het elastische gebied: σ = Eε.

Soorten Belastingen en Vervormingen

Mechanica van Materialen behandelt verschillende soorten belastingen en de bijbehorende vervormingen:

Trekbelasting: Veroorzaakt rek in de lengterichting en krimp in de breedterichting.
Drukbelasting: Veroorzaakt krimp in de lengterichting en uitzetting in de breedterichting.
Schuifbelasting: Veroorzaakt een hoekverandering (schuifrek) in het materiaal.
Buigbelasting: Veroorzaakt zowel trek- als drukspanningen in het materiaal, afhankelijk van de positie ten opzichte van de neutrale as.
Torsie: Veroorzaakt een verdraaiing van het materiaal.

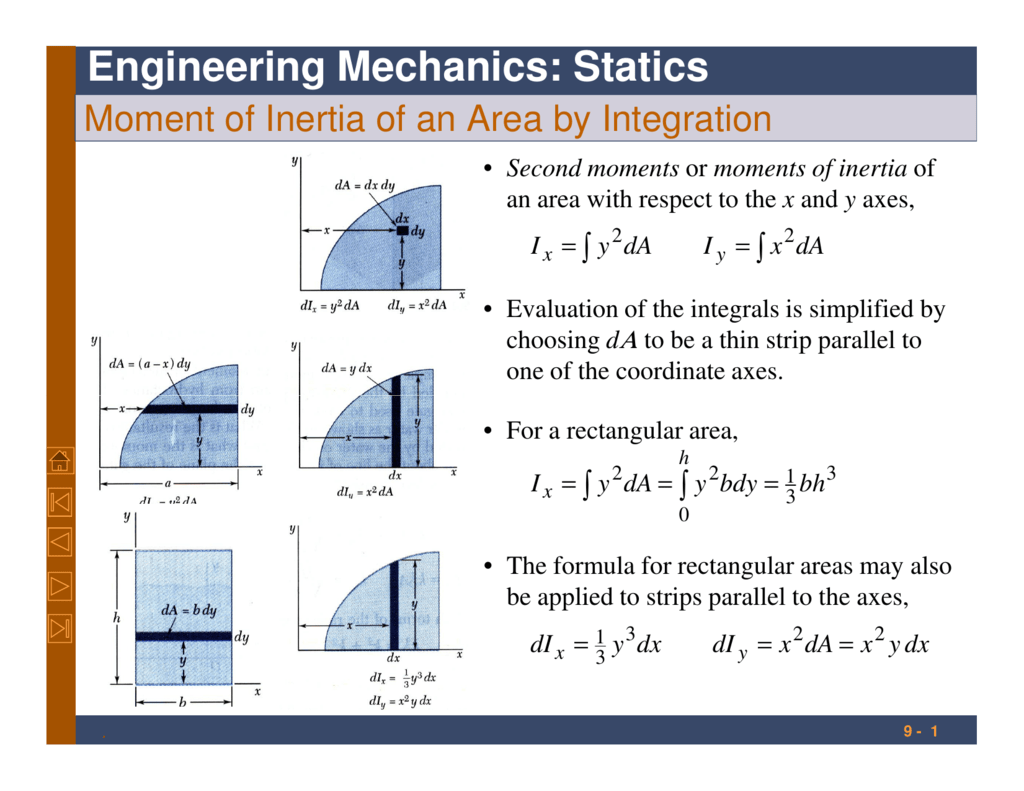
Het traagheidsmoment (I) is een belangrijke eigenschap bij buigbelasting. Het vertegenwoordigt de weerstand van een doorsnede tegen buiging. Een groter traagheidsmoment betekent een grotere weerstand tegen buiging.

Toepassingen van Mechanica van Materialen

Mechanica van Materialen is essentieel voor:

Ontwerpen van structurele componenten: Zoals balken, kolommen en assen, om ervoor te zorgen dat ze de verwachte belastingen kunnen weerstaan zonder te bezwijken.
Materiaalkeuze: Het selecteren van het juiste materiaal voor een bepaalde toepassing op basis van zijn sterkte, stijfheid en andere eigenschappen.
Analyse van faalmechanismen: Het begrijpen van hoe en waarom materialen falen onder belasting, om faalpreventie te verbeteren.

Een voorbeeld is het ontwerpen van een as in een machine. De as moet bestand zijn tegen zowel torsie (door het overbrengen van koppel) als buiging (door de gewichten van de onderdelen die de as draagt). Mechanica van Materialen wordt gebruikt om de diameter van de as te bepalen die nodig is om te voorkomen dat deze bezwijkt onder de maximale verwachte belasting. Hierbij wordt rekening gehouden met de materiaaleigenschappen van de as (zoals de vloeigrens en de treksterkte) en de geometrie van de as (zoals de diameter en de lengte).

Het Belang van SI-Eenheden

Het gebruik van SI-eenheden is van cruciaal belang in zowel Statica als Mechanica van Materialen. SI-eenheden zorgen voor consistentie en duidelijkheid in berekeningen en communicatie, en ze worden internationaal erkend en gebruikt.

Waarom SI-Eenheden?

Consistentie: SI-eenheden zijn gebaseerd op een consistent systeem van basiseenheden, waardoor er minder kans is op fouten door conversies tussen verschillende eenheidssystemen.
Internationale Standaard: SI-eenheden zijn de internationale standaard voor wetenschappelijke en technische toepassingen, waardoor de communicatie en samenwerking tussen ingenieurs en wetenschappers wereldwijd wordt vergemakkelijkt.
Eenvoud: SI-eenheden zijn gebaseerd op het decimale stelsel, waardoor berekeningen en conversies eenvoudiger zijn.

Het correct gebruiken van SI-eenheden, zoals Newton (N) voor kracht, Pascal (Pa) voor spanning en meter (m) voor lengte, is essentieel voor accurate en betrouwbare resultaten.

Voorbeeld: In de bouw wordt vaak beton gebruikt. Om te bepalen of een betonnen balk de juiste afmetingen heeft voor de te verwachten belasting, moet de spanning in de balk berekend worden. Dit gebeurt in Pascal (Pa) of MegaPascal (MPa). Als de berekening met bijvoorbeeld Engelse eenheden zou gebeuren, zou dit tot verwarring en potentieel gevaarlijke fouten leiden.

Conclusie

Statica en Mechanica van Materialen zijn fundamentele disciplines in de engineering. Door deze principes te begrijpen en ze toe te passen met behulp van SI-eenheden, kunnen ingenieurs veilige, efficiënte en duurzame structuren en componenten ontwerpen en analyseren. Of het nu gaat om het ontwerpen van een brug, een machine of een vliegtuig, de kennis van deze disciplines is van onschatbare waarde.

Neem de uitdaging aan om uw kennis van Statica en Mechanica van Materialen te verdiepen. Oefen met het oplossen van problemen, experimenteer met softwaretools en blijf op de hoogte van de nieuwste ontwikkelingen in het vakgebied. Uw inzet zal bijdragen aan innovatieve en veilige oplossingen voor de uitdagingen van de toekomst!