Wat Zijn Ribben In Wiskunde

Heb je je ooit afgevraagd hoe wiskunde, iets wat soms zo abstract kan aanvoelen, eigenlijk verbonden is met de wereld om ons heen? Veel mensen worstelen met wiskundige concepten, en dat is begrijpelijk. Soms lijkt het alsof wiskunde een geheimtaal is die alleen door een select groepje wordt begrepen. Een van die concepten die vaak vragen oproept, is dat van "ribben". In dit artikel gaan we dieper in op wat ribben in de wiskunde precies zijn, en we proberen de materie zo helder mogelijk uit te leggen, zodat je hopelijk met een beter begrip achterblijft.

Wat zijn Ribben Eigenlijk?

De term "ribbe" komt voor in verschillende gebieden van de wiskunde, maar de betekenis is overal min of meer hetzelfde. Het gaat om een lijnsegment dat twee hoekpunten (of vertices) verbindt. Laten we eens kijken naar enkele specifieke contexten:

Ribben in de Meetkunde

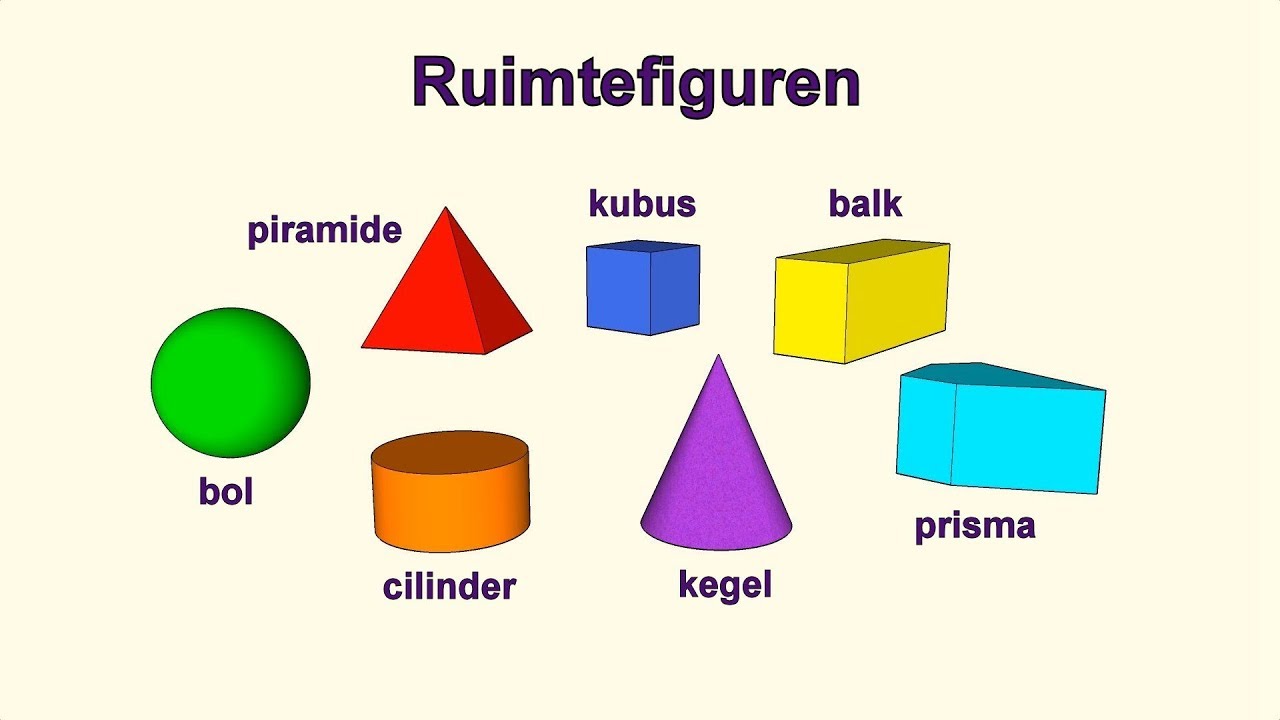
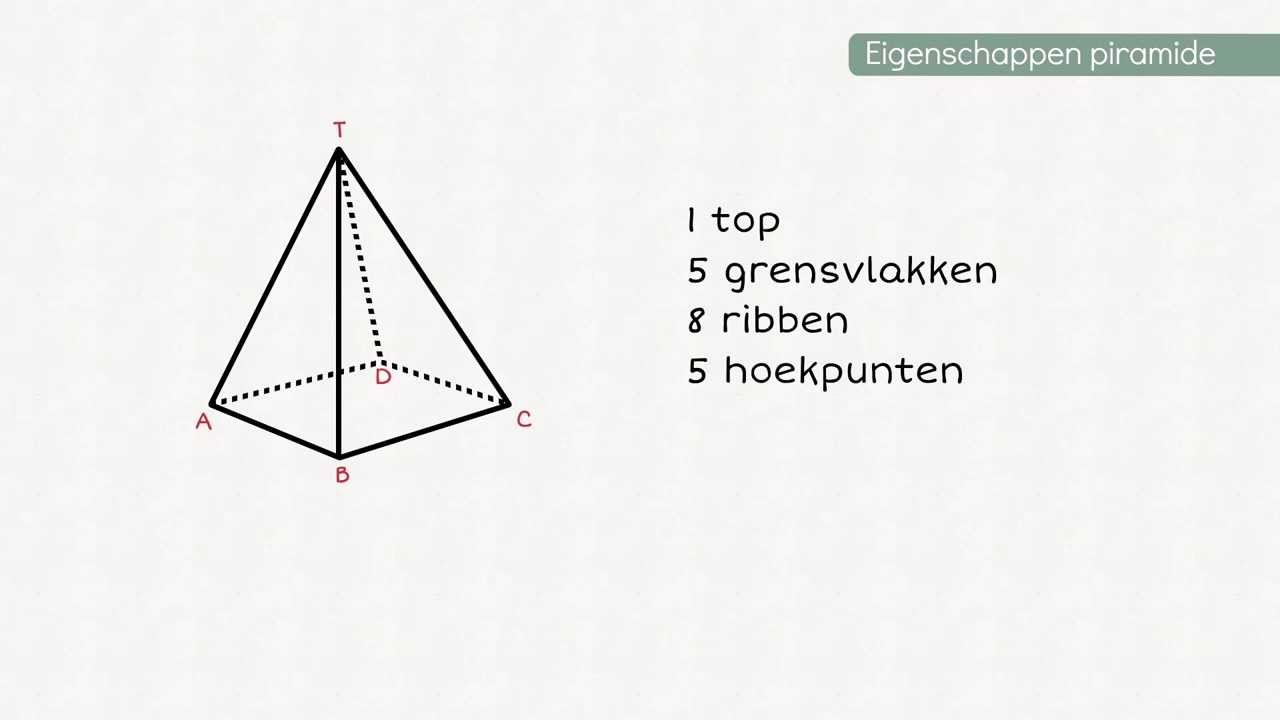
In de meetkunde, en dan vooral in de 3D-meetkunde, verwijst de term "ribbe" meestal naar een lijnsegment dat twee vlakken van een polyeder verbindt. Een polyeder is een 3D-object met platte vlakken, rechte ribben en hoekpunten. Denk aan een kubus, een piramide, of een prisma.

Kubus: Een kubus heeft 12 ribben. Elke ribbe verbindt twee aangrenzende vlakken.
Piramide: Een vierzijdige piramide (met een vierkant als basis) heeft 8 ribben.
Prisma: Een driehoekig prisma heeft 9 ribben.

Het is belangrijk om te onthouden dat de ribben de "randen" vormen waar de vlakken samenkomen. Zonder ribben zouden de vlakken geen gesloten 3D-object vormen.

Ribben in Grafentheorie

De grafentheorie is een tak van de wiskunde die zich bezighoudt met het bestuderen van grafen. Een graaf bestaat uit een verzameling knopen (of vertices) en ribben (of edges) die deze knopen verbinden. In deze context vertegenwoordigen de ribben relaties tussen de knopen.

Knoop: Een knoop kan een object, persoon, plaats, of elk ander concept vertegenwoordigen.
Ribbe: Een ribbe vertegenwoordigt een verbinding of relatie tussen twee knopen.

Voorbeeld: Stel je een sociaal netwerk voor. Elke persoon is een knoop, en een ribbe tussen twee knopen betekent dat die twee personen vrienden zijn.

Ribben in een graaf kunnen gericht of ongericht zijn. Een gerichte ribbe heeft een richting (bijvoorbeeld een pijl) die aangeeft dat de relatie slechts in één richting geldt. Een ongerichte ribbe heeft geen richting, wat betekent dat de relatie in beide richtingen geldt.

Verbinding met Andere Wiskundige Concepten

Het concept van "ribben" is fundamenteel en komt terug in veel andere wiskundige gebieden, zoals:

Topologie: De topologie bestudeert de eigenschappen van objecten die behouden blijven onder continue vervormingen (zoals rekken, buigen en draaien). Het aantal ribben in een object (of een graaf) is een belangrijke topologische invariant.
Lineaire Algebra: Matrices kunnen worden gebruikt om grafen te representeren, waarbij de elementen van de matrix aangeven of er een ribbe is tussen twee knopen.
Discrete Wiskunde: De grafentheorie is een belangrijk onderdeel van de discrete wiskunde, die zich bezighoudt met objecten die afzonderlijk en discreet zijn, in plaats van continu.

Real-World Impact: Meer dan alleen Theorie

Je vraagt je misschien af: "Waarom is dit belangrijk? Wat kan ik ermee in het echte leven?" Nou, de concepten die te maken hebben met ribben hebben een enorme impact op verschillende gebieden:

Netwerkanalyse: De grafentheorie, met zijn knopen en ribben, wordt gebruikt om sociale netwerken, computernetwerken, transportnetwerken en nog veel meer te analyseren. Dit helpt om patronen te ontdekken, bottlenecks te identificeren en de efficiëntie te verbeteren. Denk aan het optimaliseren van routes voor bezorgdiensten of het analyseren van de verspreiding van informatie op sociale media.
Computer Graphics: Ribben zijn essentieel voor het modelleren en renderen van 3D-objecten in computergraphics. Zonder ribben zouden we geen realistische afbeeldingen van objecten kunnen maken in games, films of simulaties.
Circuitontwerp: In de elektronica worden ribben gebruikt om de verbindingen tussen componenten in een circuit te representeren. Dit helpt ingenieurs bij het ontwerpen en analyseren van complexe circuits.
Optimalisatieproblemen: Veel optimalisatieproblemen, zoals het vinden van het kortste pad tussen twee punten of het toewijzen van resources aan taken, kunnen worden gemodelleerd met behulp van grafen en ribben.

Kortom, de studie van ribben helpt ons om complexe systemen te begrijpen, te analyseren en te optimaliseren. Het is een krachtig hulpmiddel dat in talloze toepassingen wordt gebruikt, van het optimaliseren van routes tot het ontwerpen van betere computers.

Counterpoints: Is het Altijd Zo Simpel?

Hoewel we de basisprincipes van ribben hebben besproken, is het belangrijk om te erkennen dat er complexiteiten zijn. In sommige gevallen kan de definitie van een ribbe variëren afhankelijk van de specifieke context. Bijvoorbeeld:

Gewogen Grafen: In een gewogen graaf heeft elke ribbe een gewicht, dat bijvoorbeeld de afstand, de kosten of de capaciteit van de verbinding kan vertegenwoordigen. Dit maakt de analyse complexer, maar ook realistischer voor veel toepassingen.
Hypergrafen: In een hypergraaf kan een ribbe meer dan twee knopen verbinden. Dit is handig voor het modelleren van situaties waarin meerdere entiteiten tegelijkertijd betrokken zijn bij een relatie.
Multigrafen: In een multigraph kunnen er meerdere ribben tussen twee knopen bestaan. Dit kan worden gebruikt om verschillende soorten relaties tussen dezelfde knopen te representeren.

Het is dus belangrijk om de context te begrijpen bij het werken met ribben. De basisprincipes blijven echter hetzelfde: een ribbe vertegenwoordigt een verbinding tussen twee (of meer) entiteiten.

Hoe Kunnen We Dit Beter Begrijpen?

Het begrijpen van ribben, en wiskundige concepten in het algemeen, vereist oefening en een beetje creativiteit. Hier zijn enkele suggesties:

Visualisatie: Teken voorbeelden van grafen en polyeders. Gebruik verschillende kleuren om de ribben te markeren.
Voorbeelden uit het Dagelijks Leven: Zoek naar voorbeelden van netwerken en structuren in je omgeving. Probeer deze te modelleren met behulp van grafen en ribben.
Oefenen: Maak opgaven en los problemen op. Dit helpt om de concepten beter te begrijpen en toe te passen.
Interactieve Tools: Er zijn online tools en softwarepakketten beschikbaar waarmee je grafen kunt maken en manipuleren. Dit kan een leuke en effectieve manier zijn om de concepten te leren.

Het belangrijkste is om niet bang te zijn om fouten te maken. Wiskunde is een proces van leren en ontdekken. Wees geduldig met jezelf en geef niet op!

Een Vraag om over Na te Denken

Nu je meer weet over ribben in de wiskunde, kun je dan een toepassing bedenken waarin het concept van ribben gebruikt wordt om een probleem op te lossen dat je zelf ervaart of hebt gezien? Misschien kan deze nieuwe kennis je helpen om de wereld om je heen op een andere manier te bekijken.

Hopelijk heeft dit artikel je geholpen om het concept van "ribben" in de wiskunde beter te begrijpen. Onthoud dat wiskunde niet eng hoeft te zijn. Met een beetje moeite en de juiste aanpak kan het zelfs leuk en boeiend zijn.