Afronden Op 1 Decimaal Calculator

In de moderne wereld, waar data en precisie steeds belangrijker worden, is het afronden van getallen een cruciale vaardigheid. Of je nu bezig bent met wetenschappelijk onderzoek, financiële berekeningen, of dagelijkse taken, het correct afronden van getallen kan een groot verschil maken in de nauwkeurigheid en betrouwbaarheid van je resultaten. Een afronden op 1 decimaal calculator is een handig hulpmiddel dat deze taak vereenvoudigt en versnelt.

Waarom Afronden Belangrijk is

Afronden is het proces waarbij een getal wordt vereenvoudigd tot een waarde die dichter bij nul ligt dan de oorspronkelijke waarde, of tot een bepaalde precisie. Dit is essentieel in verschillende situaties:

Vereenvoudiging: Complexe getallen met veel decimalen kunnen onpraktisch zijn om mee te werken. Afronden maakt de getallen overzichtelijker.
Precisie: In sommige contexten is een hoge mate van precisie niet nodig of zelfs misleidend. Afronden kan de focus leggen op de significante cijfers.
Consistentie: Afronden zorgt voor consistentie in data presentatie en vergelijkingen.

De Noodzaak van Afronden op 1 Decimaal

Afronden op 1 decimaal is een veelgebruikte methode. Het biedt een balans tussen precisie en eenvoud. Dit is vaak voldoende nauwkeurig voor alledaagse toepassingen en veel professionele velden. Denk aan:

Financiën: Bedragen worden vaak afgerond op 1 decimaal, vooral bij valuta-omrekeningen en kostenberekeningen.
Statistiek: Gemiddelden en andere statistische waarden worden vaak met 1 decimaal gepresenteerd voor een heldere interpretatie.
Wetenschap: Bij metingen en experimenten is afronden op 1 decimaal soms voldoende, afhankelijk van de precisie van de meetinstrumenten.
Dagelijks leven: Bij het schatten van afstanden, gewichten of andere grootheden is afronden op 1 decimaal vaak voldoende voor een praktisch bruikbaar resultaat.

Hoe een Afronden Op 1 Decimaal Calculator Werkt

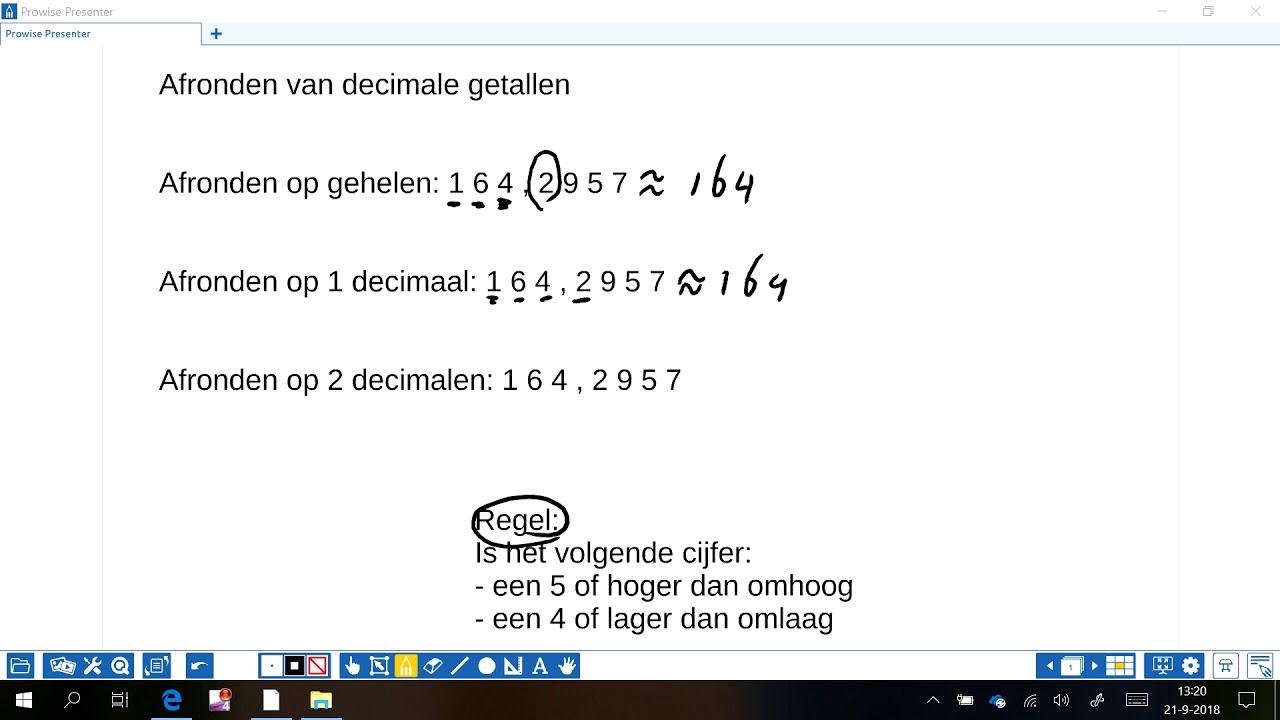
Een afronden op 1 decimaal calculator werkt volgens een eenvoudige regel: als het cijfer op de tweede decimaal 5 of hoger is, wordt het cijfer op de eerste decimaal met 1 verhoogd. Is het cijfer lager dan 5, dan blijft het cijfer op de eerste decimaal ongewijzigd.

Voorbeelden:

3.14 wordt afgerond op 3.1
3.15 wordt afgerond op 3.2
3.149 wordt afgerond op 3.1
3.151 wordt afgerond op 3.2
3.99 wordt afgerond op 4.0

De calculator automatiseert dit proces, waardoor je snel en nauwkeurig getallen kunt afronden zonder handmatige berekeningen te hoeven uitvoeren. Dit is vooral handig bij grotere datasets of complexe berekeningen.

De Voordelen van een Online Calculator

Er zijn verschillende redenen waarom het gebruik van een online afronden op 1 decimaal calculator de voorkeur heeft boven handmatige berekeningen:

Snelheid: De calculator voert de afronding direct uit, wat tijd bespaart.
Nauwkeurigheid: De calculator elimineert menselijke fouten die kunnen optreden bij handmatige berekeningen.
Gemak: Je hebt direct toegang tot de calculator via je browser, zonder dat je speciale software hoeft te installeren.
Herhaalbaarheid: Dezelfde afrondingsregels worden consistent toegepast op alle getallen.

Real-World Voorbeelden en Data

Laten we eens kijken naar enkele real-world voorbeelden waar een afronden op 1 decimaal calculator van pas kan komen:

Financiële Berekeningen

Stel je voor dat je de wisselkoers van euro naar dollar wilt berekenen. De koers is bijvoorbeeld 1.0876. Als je dit afrondt op 1 decimaal, krijg je 1.1. Dit is een bruikbare waarde voor snelle schattingen en budgettering. Bij het berekenen van de BTW op een product is afronden op 1 decimaal ook gebruikelijk. Een product kost €25,79 exclusief BTW. De BTW (21%) is €5,4159. Afgerond op 1 decimaal is dit €5,4. De totale kosten zijn dan €31,2 (25,79 + 5,4).

Statistische Analyse

In een onderzoek naar de gemiddelde lengte van een bepaalde populatie vind je de volgende data: 175.4 cm, 178.2 cm, 180.1 cm, 172.9 cm, en 182.5 cm. Het gemiddelde is 177.82 cm. Afronden op 1 decimaal geeft een gemiddelde lengte van 177.8 cm. Dit is een overzichtelijkere en gemakkelijk te interpreteren waarde dan het exacte gemiddelde.

Wetenschappelijk Onderzoek

Bij het meten van de pH-waarde van een oplossing krijg je een waarde van 7.345. Afronden op 1 decimaal levert een pH-waarde van 7.3 op. Dit is vaak voldoende nauwkeurig voor de meeste experimenten, tenzij een hogere precisie vereist is.

Dagelijkse Toepassingen

Je wilt een recept verdubbelen, maar de hoeveelheden zijn lastig af te meten. Een ingrediënt vereist 1.75 kopjes bloem. Afgerond op 1 decimaal is dit 1.8 kopjes. Dit is een veel praktischere hoeveelheid om te meten.

De Grenzen van Afronden

Hoewel afronden nuttig is, is het belangrijk om te beseffen dat het ook kan leiden tot verlies van informatie en cumulatieve fouten, vooral bij herhaalde berekeningen. Het is cruciaal om te bepalen of afronden gepast is in de context van de berekening, en zo ja, tot welke precisie. In situaties waar precisie van het grootste belang is (bijvoorbeeld in de wetenschap of de engineering), is het wellicht beter om met de oorspronkelijke waarden te werken en afronden pas toe te passen aan het einde van de berekening, als de resultaten gepresenteerd moeten worden.

Cumulatieve fouten kunnen optreden als je bijvoorbeeld veel getallen afrondt en vervolgens optelt. De kleine afrondingsfouten kunnen zich opstapelen en een significante afwijking veroorzaken van de werkelijke waarde. Daarom is het belangrijk om te overwegen of afronden in een specifieke context verantwoord is en welke impact het kan hebben op de uiteindelijke resultaten.

Alternatieve Afrondingstechnieken

Naast de standaard afrondingsmethode (afronden naar het dichtstbijzijnde getal) zijn er ook andere afrondingstechnieken die in specifieke situaties nuttig kunnen zijn:

Afronden naar beneden (floor): Hierbij wordt het getal altijd naar beneden afgerond naar het dichtstbijzijnde lagere gehele getal. Bijvoorbeeld, 3.7 wordt afgerond naar 3.0.
Afronden naar boven (ceil): Hierbij wordt het getal altijd naar boven afgerond naar het dichtstbijzijnde hogere gehele getal. Bijvoorbeeld, 3.2 wordt afgerond naar 4.0.
Afronden naar nul (truncate): Hierbij worden alle decimalen na een bepaalde precisie afgekapt, zonder naar boven of beneden af te ronden. Bijvoorbeeld, 3.149 wordt afgerond naar 3.1.

De keuze van de afrondingstechniek hangt af van de specifieke eisen van de toepassing. In sommige gevallen is het belangrijk om altijd naar beneden of naar boven af te ronden om te voldoen aan bepaalde eisen of regels.

Conclusie

Een afronden op 1 decimaal calculator is een waardevol hulpmiddel voor iedereen die regelmatig met getallen werkt. Het biedt snelheid, nauwkeurigheid en gemak, waardoor je efficiënter kunt werken en fouten kunt vermijden. Hoewel het belangrijk is om de grenzen van afronden te begrijpen en te overwegen of het gepast is in de context van de berekening, is het een onmisbare vaardigheid in vele aspecten van het leven. Maak gebruik van een online calculator om je berekeningen te vereenvoudigen en je data overzichtelijker te presenteren. Experimenteer met verschillende getallen en scenario's om vertrouwd te raken met de werking van de calculator en de impact van afronden op je resultaten. Door bewust om te gaan met afronden, kun je de betrouwbaarheid en bruikbaarheid van je berekeningen vergroten.

Probeer nu zelf een afronden op 1 decimaal calculator en ontdek hoe het jouw werk en dagelijkse taken kan vereenvoudigen! Afronden was nog nooit zo gemakkelijk!