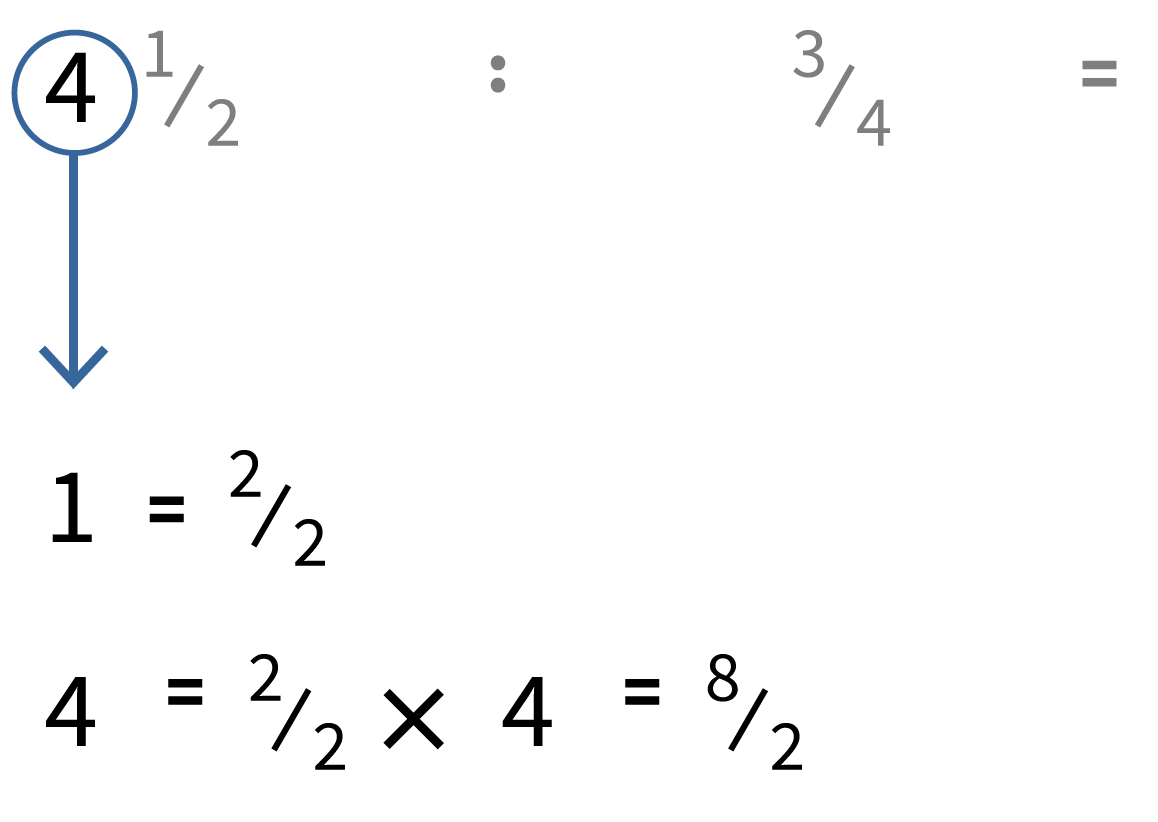Breuk Delen Door Een Breuk
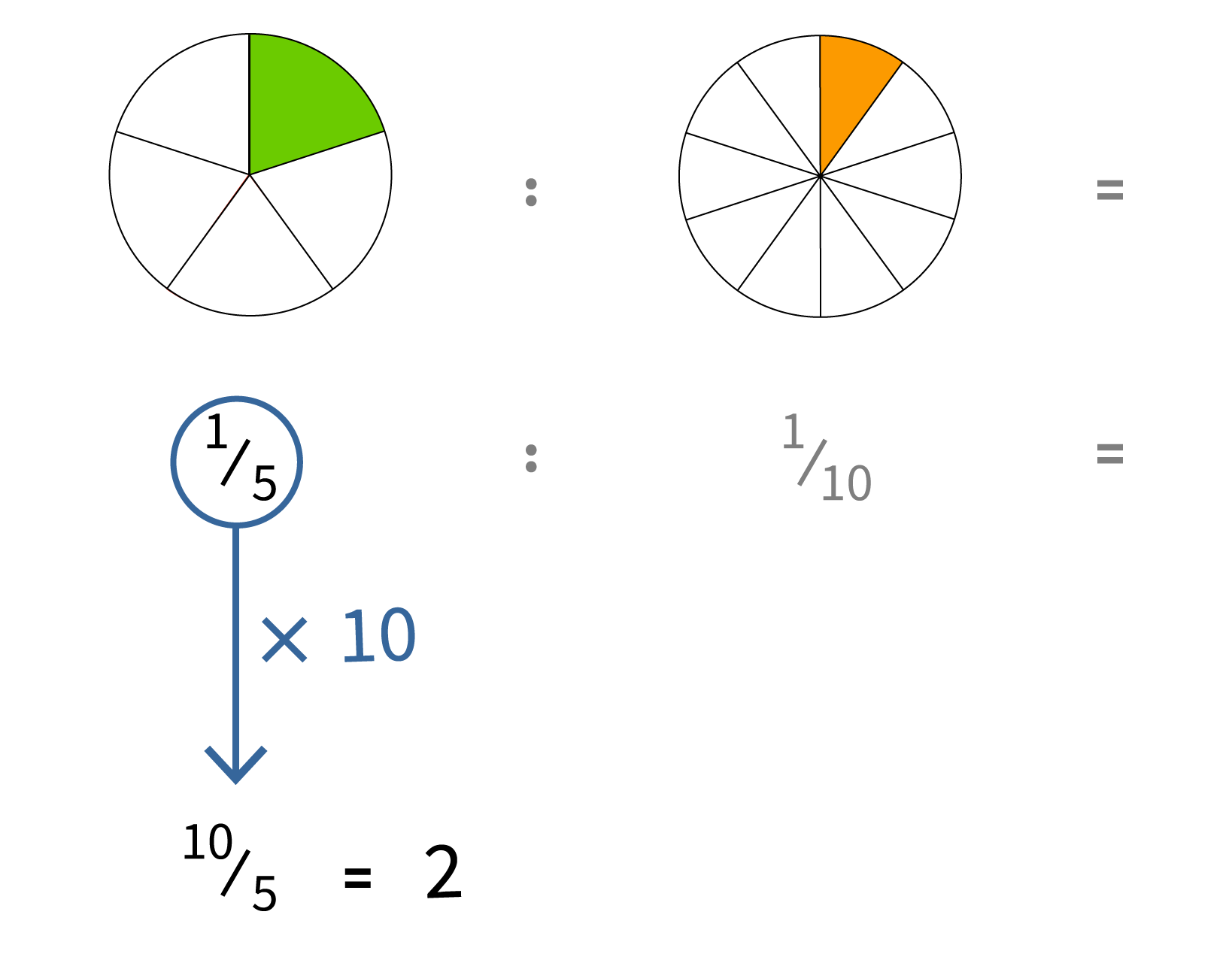
Het delen van breuken door breuken is een fundamenteel concept in de wiskunde, dat op het eerste gezicht intimiderend kan lijken. Echter, met een heldere uitleg en enkele praktische voorbeelden, kan het snel begrepen en toegepast worden. Dit artikel zal dieper ingaan op dit onderwerp, de belangrijkste principes uitleggen en laten zien hoe deze vaardigheid relevant is in de echte wereld.
Waarom is het delen van breuken belangrijk?
Het begrijpen van het delen van breuken is essentieel voor verschillende redenen. Ten eerste is het een bouwsteen voor meer geavanceerde wiskundige concepten, zoals algebra en calculus. Ten tweede, het heeft praktische toepassingen in het dagelijks leven, van het koken tot het plannen van projecten. Zonder deze basiskennis kunnen veel alledaagse problemen lastiger op te lossen zijn.
De basisprincipes van breuken delen
Een breuk is een manier om een deel van een geheel weer te geven. Het bestaat uit een teller (het getal boven de streep) en een noemer (het getal onder de streep). De noemer geeft aan in hoeveel gelijke delen het geheel is verdeeld, en de teller geeft aan hoeveel van die delen we hebben. Bijvoorbeeld, in de breuk 3/4, is 3 de teller en 4 de noemer. Dit betekent dat we 3 van de 4 gelijke delen van een geheel hebben.
Het delen van breuken lijkt misschien lastig, maar het is eigenlijk vrij eenvoudig. De sleutel is het concept van het omgekeerde van een breuk. Het omgekeerde van een breuk krijg je door de teller en de noemer te verwisselen. Bijvoorbeeld, het omgekeerde van 2/3 is 3/2.
De regel voor het delen van breuken is: vermenigvuldig met het omgekeerde. Dus, als je breuk A (a/b) deelt door breuk B (c/d), dan vermenigvuldig je breuk A met het omgekeerde van breuk B (d/c). Wiskundig gezien:
a/b ÷ c/d = a/b × d/c = a×d/b×c
Stap-voor-stap uitleg met voorbeelden
Laten we dit concept stap voor stap bekijken met enkele voorbeelden:
Voorbeeld 1: 1/2 delen door 1/4
- Identificeer de breuken: We hebben 1/2 en 1/4.
- Neem het omgekeerde van de tweede breuk: Het omgekeerde van 1/4 is 4/1 (wat gelijk is aan 4).
- Vermenigvuldig de eerste breuk met het omgekeerde van de tweede breuk: 1/2 × 4/1 = 1×4/2×1 = 4/2.
- Vereenvoudig de breuk: 4/2 = 2.
Dus, 1/2 gedeeld door 1/4 is gelijk aan 2. Dit betekent dat er 2 stukken van 1/4 in 1/2 passen.
Voorbeeld 2: 3/5 delen door 2/3
- Identificeer de breuken: We hebben 3/5 en 2/3.
- Neem het omgekeerde van de tweede breuk: Het omgekeerde van 2/3 is 3/2.
- Vermenigvuldig de eerste breuk met het omgekeerde van de tweede breuk: 3/5 × 3/2 = 3×3/5×2 = 9/10.
- Vereenvoudig de breuk: 9/10 is al in zijn eenvoudigste vorm.
Dus, 3/5 gedeeld door 2/3 is gelijk aan 9/10.
Voorbeeld 3: Een gemengde breuk delen door een breuk
Laten we 21/2 delen door 1/3.
- Zet de gemengde breuk om in een onechte breuk: 21/2 = (2 × 2 + 1) / 2 = 5/2.
- Identificeer de breuken: We hebben nu 5/2 en 1/3.
- Neem het omgekeerde van de tweede breuk: Het omgekeerde van 1/3 is 3/1 (wat gelijk is aan 3).
- Vermenigvuldig de eerste breuk met het omgekeerde van de tweede breuk: 5/2 × 3/1 = 5×3/2×1 = 15/2.
- Vereenvoudig de breuk (optioneel, zet om in een gemengde breuk): 15/2 = 71/2.
Dus, 21/2 gedeeld door 1/3 is gelijk aan 15/2 of 71/2.
Real-world voorbeelden
Het delen van breuken komt vaker voor in het dagelijks leven dan je misschien denkt. Hier zijn enkele voorbeelden:
Koken
Stel je voor dat je een recept hebt dat zegt dat je 2/3 kopje bloem nodig hebt voor één portie. Je wilt 1/4 portie maken. Om te bepalen hoeveel bloem je nodig hebt, deel je 1/4 door 2/3. Dit geeft je: 1/4 ÷ 2/3 = 1/4 × 3/2 = 3/8 kopje bloem. Dit illustreert hoe het delen van breuken je helpt om recepten te schalen.
Bouw en constructie
Een timmerman moet een plank van 3/4 meter lang in stukken van 1/8 meter snijden. Om te bepalen hoeveel stukken hij kan snijden, deelt hij 3/4 door 1/8: 3/4 ÷ 1/8 = 3/4 × 8/1 = 24/4 = 6 stukken. Dit laat zien hoe het delen van breuken handig is bij het meten en snijden van materialen.
Tijdsmanagement
Als je een taak hebt die 1/2 uur duurt en je wilt deze in stukken van 1/6 uur verdelen, dan moet je 1/2 delen door 1/6: 1/2 ÷ 1/6 = 1/2 × 6/1 = 6/2 = 3 stukken. Dit helpt je bij het plannen van je tijd en het organiseren van taken.
Financiën
Stel, je hebt een investering die een rendement van 1/5 oplevert en je wilt weten hoeveel je per kwartaal verdient. Je weet dat er 1/4 jaar in een kwartaal zit. Je deelt 1/5 door 1/4 om te bepalen wat je per kwartaal verdient: 1/5 ÷ 1/4 = 1/5 × 4/1 = 4/5 van het jaarlijkse rendement per kwartaal. Hoewel dit een simplistisch voorbeeld is, laat het zien hoe breuken gebruikt kunnen worden bij berekeningen rond rendement en tijdsperiodes.
Veelgemaakte fouten en hoe deze te vermijden
Er zijn een paar veelgemaakte fouten die mensen maken bij het delen van breuken:
- Vergeten het omgekeerde te nemen: Dit is de meest voorkomende fout. Vergeet niet om altijd het omgekeerde te nemen van de tweede breuk (de breuk waarmee je deelt) voordat je gaat vermenigvuldigen.
- Tellers en noemers verkeerd vermenigvuldigen: Zorg ervoor dat je de tellers met elkaar vermenigvuldigt en de noemers met elkaar vermenigvuldigt.
- Niet vereenvoudigen van de breuk: Na de vermenigvuldiging, vereenvoudig de resulterende breuk altijd tot de eenvoudigste vorm. Dit maakt het resultaat makkelijker te begrijpen en te gebruiken.
Conclusie en aanbevelingen
Het delen van breuken door breuken is een essentiële vaardigheid in de wiskunde en heeft tal van toepassingen in het dagelijks leven. Door de basisprincipes te begrijpen, de regel "vermenigvuldig met het omgekeerde" te onthouden en veel te oefenen, kan iedereen deze vaardigheid beheersen.
Neem de tijd om deze concepten te oefenen. Gebruik online resources, werkboeken, of vraag hulp aan een leraar of tutor. Hoe meer je oefent, hoe zelfverzekerder je zult worden in het delen van breuken. Het is niet alleen een wiskundige vaardigheid, maar ook een vaardigheid die je in veel verschillende situaties van pas kan komen.
Dus, ga aan de slag, oefen en ontdek hoe het delen van breuken je kan helpen om problemen op te lossen, zowel in de wiskunde als in de echte wereld! De kracht van breuken ligt in hun eenvoud en hun veelzijdigheid. Beheers de basis, en de rest volgt vanzelf.