Hoe Bereken Je De Amplitude

Amplitude is een fundamenteel concept in de wetenschap en techniek, van geluidsgolven en licht tot elektromagnetische signalen en mechanische trillingen. Het begrijpen van amplitude is cruciaal voor het analyseren, interpreteren en manipuleren van deze fenomenen. In dit artikel duiken we diep in de berekening van amplitude, leggen we de principes uit, en illustreren we het met praktische voorbeelden.

Wat is Amplitude Eigenlijk?

Simpel gezegd, de amplitude is de maximale uitwijking van een golf of trilling vanaf zijn evenwichtspositie. Denk aan een slinger; de amplitude is de maximale afstand die de slinger beweegt van het middenpunt. Bij een geluidsgolf is de amplitude gerelateerd aan de luidheid van het geluid. Bij licht correspondeert amplitude met de helderheid.

Het is belangrijk om te benadrukken dat amplitude altijd een positieve waarde is. Het vertegenwoordigt de grootte van de verandering, niet de richting.

Hoe Bereken Je de Amplitude?

De methode voor het berekenen van de amplitude hangt af van het type golf of trilling dat je analyseert en de beschikbare data. Hieronder beschrijven we verschillende scenario's en bijbehorende methoden.

1. Van een Grafiek:

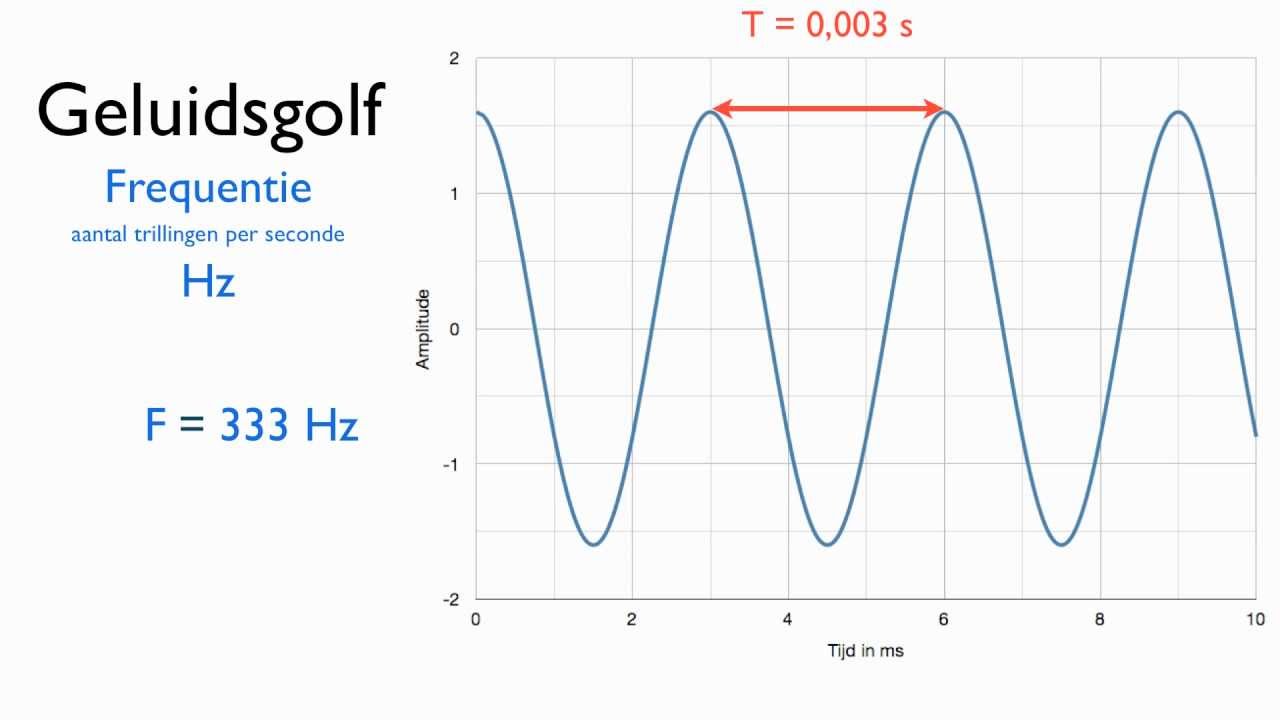
De meest visuele manier om de amplitude te bepalen is door te kijken naar een grafiek van de golf. Stel je een sinusgolf voor, weergegeven op een grafiek met de tijd op de x-as en de uitwijking (bijvoorbeeld spanning, druk, positie) op de y-as.

Om de amplitude te bepalen:

1. Zoek de evenwichtspositie. Dit is de horizontale lijn waar de golf omheen oscilleert.
2. Identificeer de piekwaarde van de golf. Dit is het hoogste punt boven de evenwichtspositie, of het laagste punt eronder (absoluut gezien).
3. De amplitude is de verticale afstand tussen de evenwichtspositie en de piekwaarde.

Voorbeeld: Stel dat een sinusgolf oscilleert rond de y = 0 lijn, en de piekwaarde is y = 5. Dan is de amplitude 5 eenheden.

2. Van een Vergelijking:

Veel golven kunnen worden beschreven door wiskundige vergelijkingen. Een veelvoorkomend voorbeeld is de sinusgolf:

y(t) = A * sin(ωt + φ)

Waar:

• y(t) is de uitwijking op tijdstip t
• A is de amplitude
• ω is de hoekfrequentie
• φ is de faseverschuiving

In deze vergelijking is de amplitude direct de coëfficiënt *A* voor de sinusfunctie. Dus als je de vergelijking hebt, is het bepalen van de amplitude eenvoudig.

Voorbeeld: Als y(t) = 10 * sin(2πt), dan is de amplitude 10.

3. Van Data Punten:

In de praktijk heb je vaak geen grafiek of vergelijking, maar een set van data punten. Bijvoorbeeld, metingen van de trilling van een machine over een bepaalde periode.

Om de amplitude te bepalen:

1. Bepaal de gemiddelde waarde van de data punten. Dit is de schatting van de evenwichtspositie.
2. Zoek de maximale afwijking van elk data punt van de gemiddelde waarde. Dit doe je door de absolute waarde van het verschil tussen elk data punt en de gemiddelde waarde te berekenen.
3. De amplitude is de grootste van deze maximale afwijkingen.

Voorbeeld: Stel dat je de volgende data punten hebt: 2, 4, 6, 4, 2. De gemiddelde waarde is (2+4+6+4+2)/5 = 3. De afwijkingen van het gemiddelde zijn: -1, 1, 3, 1, -1. De absolute waarden van de afwijkingen zijn: 1, 1, 3, 1, 1. De maximale afwijking (en dus de amplitude) is 3.

4. Bij Complexe Golven:

Niet alle golven zijn simpele sinusgolven. Sommige golven zijn complex, bestaande uit een combinatie van verschillende frequenties en amplitudes. In dit geval is de term "amplitude" minder eenduidig. Er zijn verschillende manieren om een maat voor de "grootte" van de golf te definiëren:

• Piek-tot-piek amplitude: Dit is het verschil tussen de maximale en minimale waarden van de golf.
• Root Mean Square (RMS) amplitude: Dit is een statistische maat die de gemiddelde "energie" van de golf weergeeft. Het wordt berekend door de kwadraten van de data punten te nemen, het gemiddelde van deze kwadraten te berekenen, en vervolgens de wortel van dat gemiddelde te nemen. RMS wordt vaak gebruikt bij het analyseren van geluid en trillingen.

Het kiezen van de juiste methode hangt af van de specifieke toepassing en wat je probeert te analyseren.

Real-World Voorbeelden

De berekening van amplitude is van vitaal belang in vele disciplines:

• Geluidsengineering: De amplitude van een geluidsgolf bepaalt de luidheid. Geluidstechnici gebruiken amplitude om geluidsniveaus te meten en aan te passen, bijvoorbeeld bij het mixen van muziek of het ontwerpen van geluidsisolerende materialen.
• Elektrotechniek: In de elektrotechniek vertegenwoordigt de amplitude van een wisselstroomsignaal (AC) de spanning. Het begrijpen van de amplitude is essentieel voor het ontwerpen van circuits en het analyseren van de prestaties van elektronische apparaten.
• Seismologie: Seismologen meten de amplitude van seismische golven om de sterkte van aardbevingen te bepalen. De Richter-schaal is gebaseerd op de logaritme van de amplitude van seismische golven.
• Medische beeldvorming: Bij echografie (ultrasound) wordt de amplitude van de teruggekaatste geluidsgolven gebruikt om beelden van interne organen te creëren. Verschillen in amplitude geven informatie over de dichtheid en structuur van weefsels.
• Telecommunicatie: Bij amplitude modulatie (AM) radio wordt de amplitude van de draaggolf gemoduleerd om informatie te verzenden. Het demoduleren van het signaal houdt in dat de veranderingen in amplitude worden gedetecteerd om de originele informatie te reconstrueren.

Data Voorbeeld (Geluidsgolf): Stel dat een microfoon een geluidsgolf oppikt en de volgende spanningswaarden genereert (in millivolt, mV) over een korte tijdsperiode: -2, 0, 2, 4, 2, 0, -2, -4, -2, 0. De gemiddelde waarde is 0 mV. De maximale afwijking is 4 mV. De amplitude van de geluidsgolf is dus 4 mV.

Conclusie

Het berekenen van de amplitude is een cruciale vaardigheid voor het analyseren van golven en trillingen in verschillende wetenschappelijke en technische contexten. Of het nu gaat om het interpreteren van grafieken, het werken met vergelijkingen, of het analyseren van data punten, de basisprincipes blijven hetzelfde: zoek de maximale uitwijking vanaf de evenwichtspositie. Door de verschillende methoden te begrijpen en de context van de data in overweging te nemen, kun je de amplitude nauwkeurig bepalen en waardevolle inzichten verkrijgen.

Oefen met verschillende voorbeelden en probeer zelf golven te meten of te simuleren. Experimenteer met verschillende data sets en methoden om je begrip van amplitude te verdiepen. Blijf leren en je zult merken hoe fundamenteel dit concept is in de wereld om ons heen! Verdiep je verder in de Fourier-analyse voor het analyseren van complexe golven, een krachtige tool die je in staat stelt om golven te ontleden in hun verschillende frequentiecomponenten, inclusief hun individuele amplitudes.