Hoe Bereken Je De Oppervlakte Van Een Prisma

Heb je ooit naar een Toblerone reep gekeken en je afgevraagd hoeveel papier er eigenlijk nodig is om die verpakking te maken? Of misschien ben je een dakdekker die de oppervlakte van een prismatisch dak moet berekenen om genoeg dakpannen te bestellen. In beide gevallen heb je te maken met de oppervlakte van een prisma. Het kan in eerste instantie lastig lijken, maar geen zorgen, we gaan het samen stap voor stap ontrafelen!

Het berekenen van de oppervlakte van een prisma is een vaardigheid die je verrassend vaak in het dagelijks leven tegenkomt, van het inschatten van de hoeveelheid verf die je nodig hebt voor een muur tot het bepalen van de benodigde hoeveelheid stof voor een tent. Het is niet alleen een wiskundige oefening, maar een praktische tool die je helpt om de wereld om je heen beter te begrijpen en problemen op te lossen.

Wat is een Prisma eigenlijk?

Laten we beginnen met de basis. Een prisma is een driedimensionaal object met twee identieke basisvlakken (deze kunnen elke vorm hebben, zoals een driehoek, vierkant, vijfhoek, etc.) die parallel aan elkaar liggen. Deze basisvlakken zijn verbonden door rechthoekige of parallellogramvormige zijvlakken. Je kunt een prisma zien als een "uitgerekte" versie van een tweedimensionale vorm. Denk aan een driehoek die naar achteren is getrokken, waardoor een driehoekig prisma ontstaat.

Voorbeelden van Prisma's:

Driehoekig Prisma: De eerder genoemde Toblerone reep is een perfect voorbeeld.
Vierkant Prisma (kubus of balk): Een doos, een baksteen, een suikerklontje.
Vijfhoekig Prisma: Minder alledaags, maar ze bestaan! Denk aan een speciaal ontworpen tent of een stuk architectuur.

Het belangrijkste om te onthouden is dat de basisvlakken *identiek* moeten zijn en parallel aan elkaar moeten liggen. Anders is het geen prisma!

Waarom is het Berekenen van de Oppervlakte Belangrijk?

Je denkt misschien: "Wanneer heb ik dit nou eigenlijk nodig?". Hier zijn een paar voorbeelden die de relevantie van het berekenen van de oppervlakte van een prisma illustreren:

Architectuur en Bouw: Architecten en bouwkundigen gebruiken de oppervlakteberekening om de benodigde hoeveelheid materialen (hout, glas, beton, etc.) voor gebouwen met prismatische vormen te bepalen.
Verpakkingen: Bedrijven gebruiken het om de hoeveelheid karton, plastic of ander verpakkingsmateriaal te berekenen die nodig is om hun producten te verpakken.
Engineering: Ingenieurs gebruiken het om de warmteoverdracht van prismatische componenten te berekenen.
Schilderen en Behangen: Je wilt een muur in de vorm van een prisma schilderen. De oppervlakteberekening helpt je om de juiste hoeveelheid verf te bepalen.
Educatie: Natuurlijk is het ook belangrijk voor school! Het helpt je om ruimtelijk inzicht te ontwikkelen en je wiskundige vaardigheden te verbeteren.

Kortom, de mogelijkheid om de oppervlakte van een prisma te berekenen is een nuttige vaardigheid in veel verschillende disciplines en situaties.

De Formule voor de Totale Oppervlakte

Nu komen we bij de kern van de zaak: hoe berekenen we die oppervlakte? De formule voor de *totale* oppervlakte van een prisma is eigenlijk vrij eenvoudig:

Totale Oppervlakte = 2 * (Oppervlakte van het Basisvlak) + (Omtrek van het Basisvlak) * (Hoogte van het Prisma)

Laten we deze formule in stukken breken:

2 * (Oppervlakte van het Basisvlak): Dit betekent dat je de oppervlakte van *één* van de basisvlakken berekent en dat vermenigvuldigt met 2 (omdat er twee identieke basisvlakken zijn).
(Omtrek van het Basisvlak): Dit is de totale lengte van alle zijden van het basisvlak. Je telt alle zijden van de vorm bij elkaar op.
(Hoogte van het Prisma): Dit is de afstand tussen de twee basisvlakken. Denk eraan, dit is niet noodzakelijk de verticale hoogte, maar de *loodrechte* afstand tussen de twee basisvlakken.

Het is belangrijk om te onthouden dat de oppervlakte van het basisvlak afhankelijk is van de vorm van het basisvlak. Hier zijn een paar veelvoorkomende voorbeelden:

Driehoekig Basisvlak: Oppervlakte = (1/2) * basis * hoogte (van de driehoek)
Vierkant Basisvlak: Oppervlakte = zijde * zijde
Rechthoekig Basisvlak: Oppervlakte = lengte * breedte
Cirkelvormig Basisvlak (cilinder): Oppervlakte = π * r² (waarbij r de straal is)

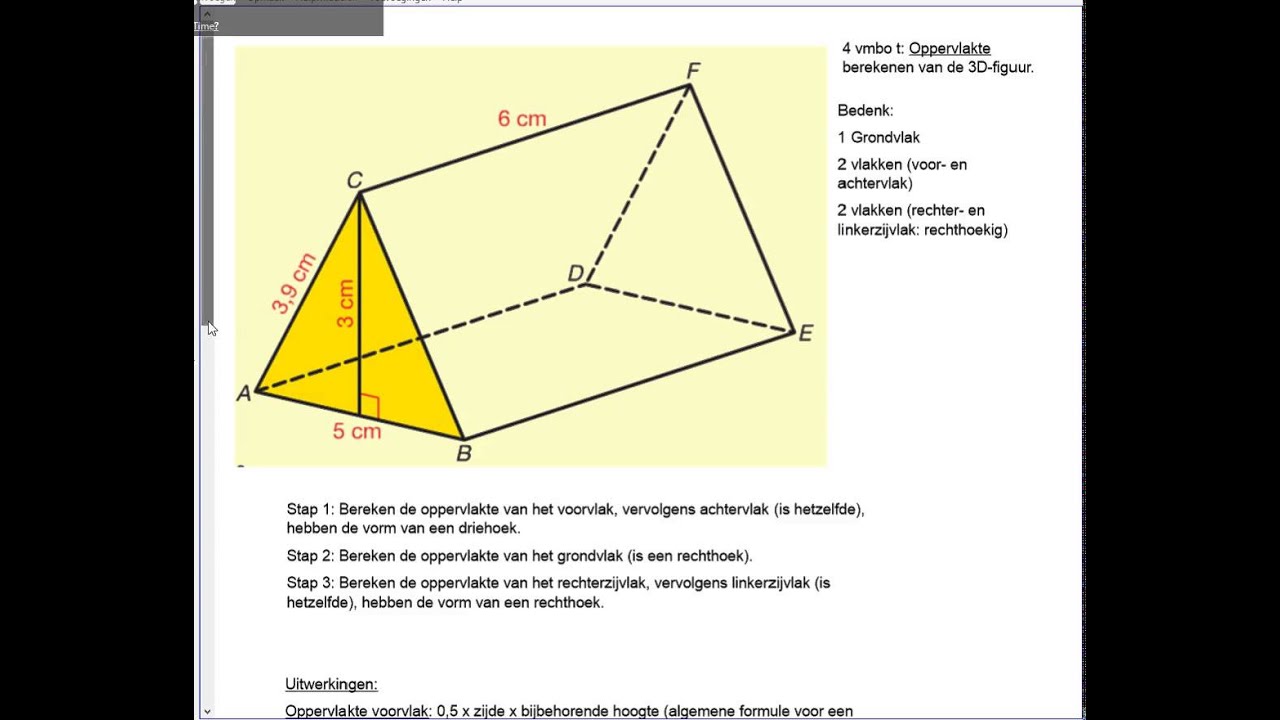
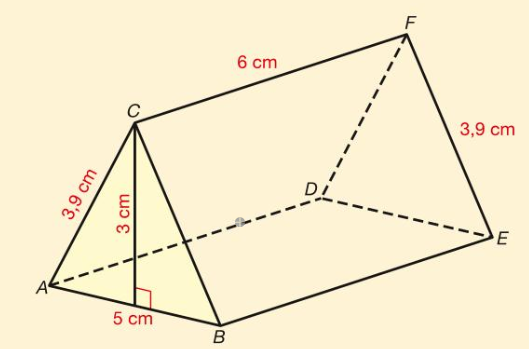
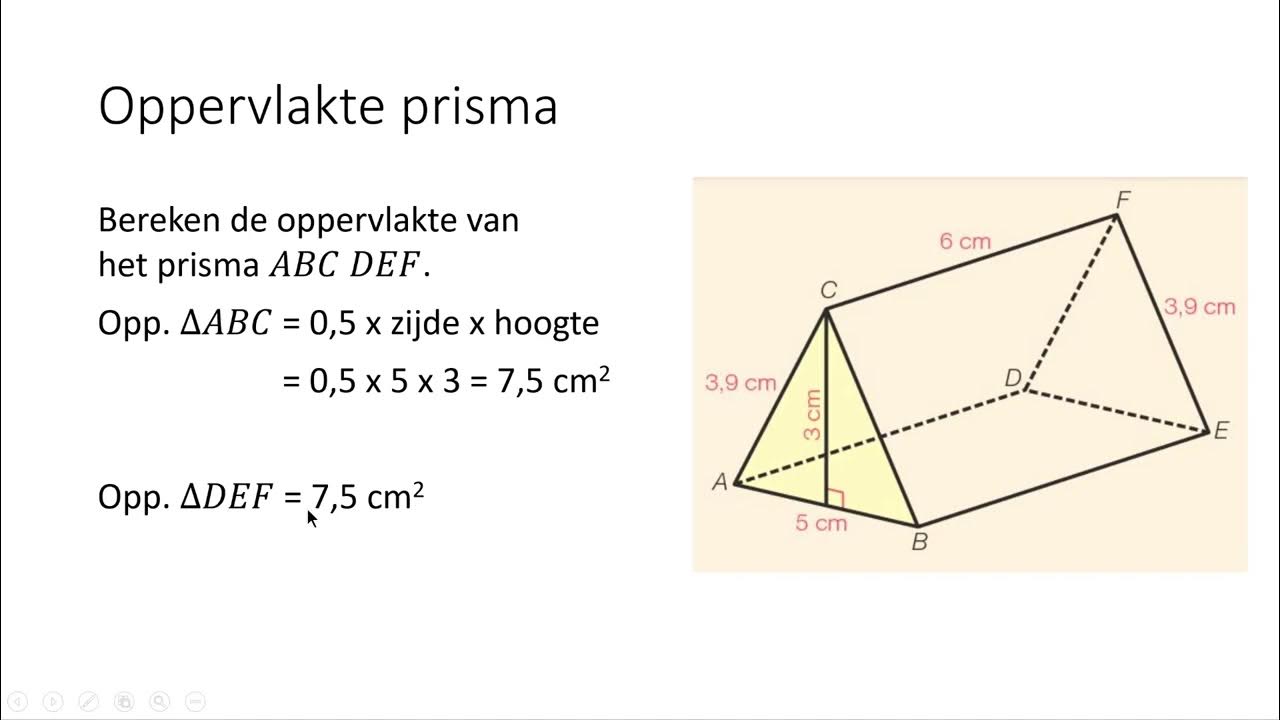
Stap voor Stap: De Oppervlakte Berekenen

Laten we de stappen eens doorlopen met een voorbeeld: een driehoekig prisma. Stel dat het basisvlak een gelijkzijdige driehoek is met een zijde van 5 cm en een hoogte van 4 cm. De hoogte van het prisma is 10 cm.

Bereken de Oppervlakte van het Basisvlak:
Oppervlakte = (1/2) * basis * hoogte = (1/2) * 5 cm * 4 cm = 10 cm²
Bereken de Omtrek van het Basisvlak:
Omtrek = 5 cm + 5 cm + 5 cm = 15 cm
Gebruik de Formule:
Totale Oppervlakte = 2 * (Oppervlakte van het Basisvlak) + (Omtrek van het Basisvlak) * (Hoogte van het Prisma)

Totale Oppervlakte = 2 * (10 cm²) + (15 cm) * (10 cm) = 20 cm² + 150 cm² = 170 cm²

Dus, de totale oppervlakte van dit driehoekige prisma is 170 cm².

Valkuilen en Aandachtspunten

Bij het berekenen van de oppervlakte van een prisma zijn er een paar valkuilen waar je op moet letten:

Verkeerde Eenheden: Zorg ervoor dat alle metingen in dezelfde eenheden zijn (bijvoorbeeld allemaal in centimeters of allemaal in meters) voordat je de berekening uitvoert.
Verkeerde Hoogte: Gebruik de *loodrechte* hoogte van het prisma, niet een schuine lengte.
Verkeerde Formule voor het Basisvlak: Gebruik de juiste formule voor het berekenen van de oppervlakte van het specifieke basisvlak (driehoek, vierkant, enz.).
Het vergeten van de eenheid: Vergeet niet om de eenheid van de oppervlakte (bijvoorbeeld cm², m², enz.) te vermelden.

Alternatieve Manieren van Denken (Counterpoint)

Sommigen beweren dat de formule voor de oppervlakte van een prisma onnodig complex is en dat het eenvoudiger is om simpelweg alle afzonderlijke vlakken te berekenen en bij elkaar op te tellen. Hoewel dit zeker mogelijk is, en in sommige gevallen (bijvoorbeeld bij een prisma met een zeer onregelmatige basis) zelfs de beste aanpak kan zijn, is de formule over het algemeen efficiënter, vooral bij prisma's met regelmatige basisvlakken. Het dwingt je ook om na te denken over de relatie tussen de verschillende onderdelen van het prisma (basisvlak en hoogte), wat een dieper begrip bevordert.

Bovendien is de formule een handig hulpmiddel voor het programmeren van computers om de oppervlakte van prisma's te berekenen. Een algoritme dat de formule gebruikt, is over het algemeen efficiënter dan een algoritme dat elk vlak afzonderlijk berekent.

De Praktijk Brengt Meester

Net als bij elke wiskundige vaardigheid, is oefening essentieel. Probeer verschillende voorbeelden te vinden, van eenvoudige tot complexere, en oefen met het berekenen van de oppervlakte. Gebruik online calculators om je antwoorden te controleren, maar probeer eerst zelf de berekening uit te voeren. Hoe meer je oefent, hoe sneller en zekerder je zult worden.

Oefenopgaven:

Bereken de oppervlakte van een rechthoekig prisma met een basis van 8 cm x 6 cm en een hoogte van 12 cm.
Bereken de oppervlakte van een driehoekig prisma met een basis van een gelijkzijdige driehoek met een zijde van 7 cm en een hoogte van 6 cm, en een hoogte van het prisma van 9 cm.
Bereken de oppervlakte van een cilinder met een straal van 4 cm en een hoogte van 15 cm. (Let op: een cilinder is een speciaal geval van een prisma met een cirkelvormig basisvlak).

Conclusie

Het berekenen van de oppervlakte van een prisma is niet zo ingewikkeld als het in eerste instantie lijkt. Door de formule te begrijpen en te oefenen, kun je deze vaardigheid beheersen en toepassen in verschillende praktische situaties. Van het schatten van de benodigde verf tot het ontwerpen van verpakkingen, de mogelijkheden zijn eindeloos. Blijf oefenen, stel vragen en laat wiskunde je niet intimideren!

Nu je weet hoe je de oppervlakte van een prisma berekent, welke prismatische objecten kom je in je dagelijks leven tegen en zou je de oppervlakte van willen berekenen?